Siméon Denis Poisson
galleggiamento di un prisma

S. D. Poisson 1781-1840
Il "Traité de Mécanique" di Poisson è un trattato di Meccanica Razionale che, all'epoca, ebbe larga diffusione e nel quale sono presenti alcuni problemi (non molti) che si possono risolvere senza far ricorso ai metodi propri dell'Analisi Matematica.
Quanto segue è uno di questi problemi riguardante il galleggiamento dei corpi.
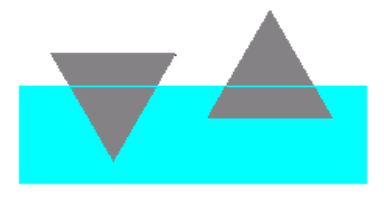
Un solido omogeneo di densità inferiore a quella del liquido in cui è immerso galleggia quando:
- il baricentro del corpo e quello del liquido spostato sono posti sulla stessa
    verticale (il baricentro del liquido spostato coincide con il baricentro della
    parte immersa);
- per il principio di Archimede deve essere

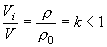
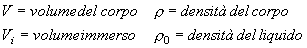
Quindi la posizione del corpo diventa un problema puramente geometrico che può essere così enunciato:

“Tagliare un corpo con un piano in modo che il volume di una sua parte stia al volume totale in un rapporto k assegnato e che i baricentri delle due parti si trovino su una stessa perpendicolare al piano secante.”

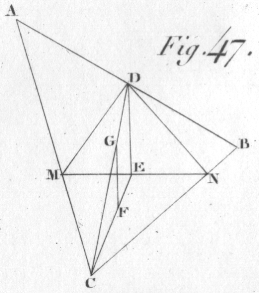
Se il corpo ha la forma di un prisma retto a base triangolare che galleggia con le basi perpendicolari alla superficie del liquido si può fare astrazione dalla altezza del prisma stesso e la questione si riduce ad un problema di geometria piana.
Sia ABC una delle basi del prisma e consideriamo un solo vertice C immerso nel liquido il cui livello è dato da MN. Posti:
Detto D il punto medio di AB, tracciato CD e preso DG = DC/3, si ha che G è il baricentro di ABC. Ancora se E è punto medio di MN, tracciato EC e preso EF = EC/3 allora F è il baricentro di MNC. Ne risulta che i triangoli DCE e GCF hanno i lati in proporzione quindi GF e DE sono paralleli. Ma GF è perpendicolare a MN quindi anche DE lo è e il triangolo MDN risulta isoscele sulla base MN quindi MD = DN. Allora posto CD = m per il teorema di Carnot si ha:
da cui segue
Per il principio di Archimede dal rapporto delle aree dei triangoli ABC e MNC si ha
da cui xy = kab.
Quindi la condizione di galleggiamento si ottiene dalla soluzione del sistema

che conduce all’equazione

Il problema si semplifica di molto se il triangolo ABC è isoscele di vertice C e in particolare se ABC è equilatero di lato l ; allora l’equazione diventa
Questa equazione ammette due radici reali e due complesse coniugate; l'unica radice che interessa è quella reale e positiva
Nel caso il triangolo equilatero ABC abbia due vertici A, B immersi, preso come riferimento ancora il vertice C, non è difficile provare che
L’evidente simmetria che si nota nella figura deriva dall’aver scelto k = 1/2.