Prismatoidi
Seguendo il lavoro di Theodor Wittstein (1816-1894), Das Prismatoid, Hannover, 1860, riassumiamo brevemente la dimostrazione che permette di arrivare alla formula del volume di questi poliedri.

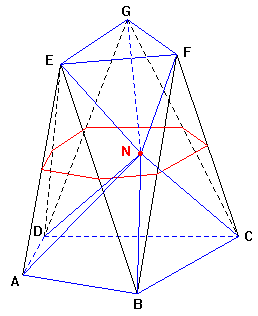
Il prismatoide è un solido poliedrico i cui vertici appartengono all'uno o all'altro dei due piani paralleli su cui si trovano le basi formate da due poligoni arbitrari. Le facce laterali, in generale, sono dei triangoli o dei trapezoidi.

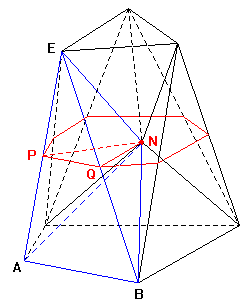
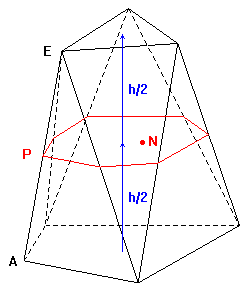
Per comodità prendiamo come basi due poligono convessi posti su due piani paralleli e per dedurre la formula del volume sezioniamo il solido con un piano equidistante dei piani sui quali giacciono le basi. Se h è l'altezza del prismatoide la sezione mediana (in rosso), posta a distanza h/2 dalle basi, risulta essere un poligono convesso i cui vertici bisecano gli spigoli laterali del solido: EP = PA.
 
Chiamate S1 l'area della base ABCD, e S3 l'area della base EFG, prendiamo un punto N appartenente alla sezione intermedia del solido. Rimangono così definite due piramidi: NABCD e NEFG, entrambe di altezza h/2, delle quali è semplice determinare i volumi.

 
Consideriamo ora la piramide ENPQ che ha come base il triangolo NPQ appartenente alla sezione intermedia, altezza h/2 e la faccia EPQ appartenete alla faccia laterale EAB del prismatoide. Chiamata si l'area del triangolo NPQ si ha che il volume della piramide ENPQ è dato da

Osserviamo che la piramide NEAB ha come base la faccia EAB del prismatoide ed è costituita dai due triangoli simili EAB e EPQ aventi i lati corrispondenti uno doppio dell'altro quindi, per quanto riguarda le aree dei triangoli, risulta  S(EAB) = 4S(EPQ). Le piramidi NEPQ e NEAB hanno, rispetto al piano della faccia EAB la medesima distanza, ne risulta che le due piramidi hanno un volume uno quadruplo dell'altro, dunque detto Vi il volume della piramide NEAB e tenuto conto che il volume della piramide NEPQ è stato determinato sopra si ha

Chiamata con S2  l'area della sezione intermedia e sommando i volumi  Vi sul numero i dei lati del poligono che costituisce questa sezione si ottiene

Possiamo ora ottenere il volume V del prismatoide come somma dei tre volumi ottenuti: V = V1 + V2 + V3 , cioè

 
Se le basi del prismatoide sono due poligoni simili con i lati corrispondenti paralleli il solido diventa un tronco di piramide, in questo caso tra l'area S2 della sezione mediana e le aree S1 ed S3 delle basi sussiste la relazione

che sostituita nell'espressione del volume del prismatoide trovata fornisce la nota formula del volume del tronco di piramide