Probabilità geometrica II
Joseph Wolstenholme (1829-1891)
 

« Mathematical Problems by Wostenholme »
 (London, 1878: Quest. 1945)
 
Un segmento RS è diviso in tre parti prendendo su di esso a caso due punti X ed Y. Determinare la probabilità che l'area del quadrato costruito sul segmento RX, sia minore dell'area del rettangolo costruito con i restanti due segmenti XY e YS.

 
 
Definite le quantità u = RX, v = XY  e  w = YS, ciascuna di esse è maggiore o uguale a zero, minore o uguale a RS , e la loro somma vale

u + v + w = RS
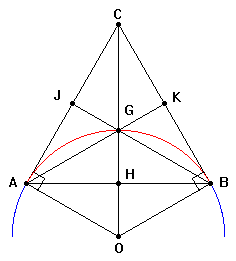
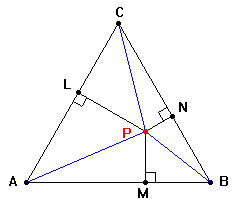
Una situazione analoga si ha per i punti interni di un triangolo equilatero per quanto riguarda la somma delle distanze di un punto P dai lati. La relazione si dimostra facilmente osservando che la somma delle aree dei triangoli APB, BPC e CPA è pari all'area del triangolo equilatero ABC avente il lato AB = 2a.
Posti: PM = u, PN  = v e PL = w si ha

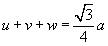Quindi possiamo identificare RS con  l'altezza di un opportuno triangolo equilatero ABC di lato AB = 2a.
Il problema ci chiede la probabilità che sia

.
 
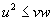Fissato un sistema di riferimento cartesiano con origine in H punto medio di AB e con l'asse delle ascisse solidale con il lato AB del triangolo equilatero, sia P(x, y) un punto interno al triangolo equilatero, scritte le equazioni delle rette alle quali appartengono il lati AC e BC , utilizzando la formula della distanza punto retta si ottiene

e sostituendo in

si arriva all'equazione di una circonferenza di equazione

che ha centro in

e raggio
La circonferenza passa per il centro G e per i vertici A e B del triangolo equilatero e nei vertici è tangente ai lati AC e BC; quindi anche il triangolo COB  è metà di un equilatero dunque l'angolo COB = 60° , ne risulta che l'angolo AOB = 120°. Siamo arrivati alla conclusione che i quadrati costruiti sul segmento RX che hanno un'area minore o uguale all'area dei rettangoli costruiti con i segmenti XY e YS corrispondono ai punti comuni ad un triangolo equilatero e ad un cerchio definito dalla circonferenza che abbiamo appena trovato. I punti interni al triangolo equilatero rappresentano tutti i quadrati e i rettangoli che si possono ottenere dividendo un dato segmento RS in tre parti prendendo su di esso a caso due punti X ed Y. Allora la probabilità cercata è il rapporto tra l'area del segmento di cerchio definito dalla corda AB e dall'arco AGB e l'area del triangolo equilatero ABC .

L'area del segmento di cerchio vale

  

l'area del triangolo equilatero vale
  e la probabilità cercata è