Proiettiva

Lazare Carnot (1753-1823)

Dal volume "Essai sur la Géométrie de la règle et de l'équerre", Paris, 1890, di G. de Longchamp riprendiamo un teorema di geometria proiettiva.

Gaston Gohierre de Longchamps detto "Elgé" (1842-1906), dopo i suoi studi di matematica si dedicò all'insegnamento nei licei francesi fino a giungere alla cattedra di "mathématiques spéciales" del "Lycée St. Louis" a Parigi. Nel 1882 prese la direzione della rivista "Journal de Mathématiques Élémentaires et Spéciales", fondata da Bourget, che diresse fino al 1898. Pubblico' diversi volumi di matematica dedicati principalmente all'insegnamento e diversi articoli specialistici firmati con il suo pseudonimo. Nel 1888 fu nominato preside del St. Louis incarico che mantenne fino al 1897.

Il problema che ci interessa è chiamato "problema della piattaforma" ed appartiene alla famiglia di problemi mediante i quali si determina la distanza tra due punti uno dei quali risulta inaccessibile. In particolare in questo problema per determinare la distanza cercata si potranno effettuare misure di segmenti che appartengono soltanto ad una regione limitata detta piattaforma che è distante dal punto inaccessibile.

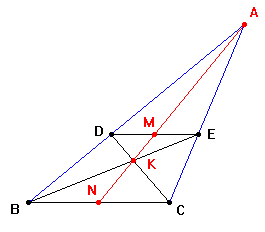
Il problema, con tecniche diverse, è stato risolto sia da Chasles che da Carnot. A noi interessa in particolare la soluzione di Carnot e, seguendo l'indirizzo di Longchamp, lo risolveremo senza fare ricorso esplicito alla geometria proiettiva. Bisogna però ricordare che il problema si colloca naturalmente in ambito proiettivo e risulta essere una semplice proprietà del quadrilatero completo. Questa figura geometrica che si deve a Carnot e' costituita da quattro rette complanari (lati), di cui tre non concorrono mai in un punto, e da sei punti (vertici) di intersezioni dei lati a due a due.

Sia A il punto inaccessibile e dai punti B, D, E, C di una piattaforma con DE parallelo a BC realizziamo la figura di sinistra. Dalla similitudine dei triangoli ADE e ABC si ha

Dai triangoli simili DEK e BCK si ottiene

e dai triangoli simili MEK e NBK

I tre risultati presi congiuntamente conducono a

che è possibile riscrivere come

Dunque il segmento AD e' medio armonico tra i segmenti AM e AN.

Nel linguaggio della geometria proiettiva questo corrisponde ad affermare che: in un quadrilatero piano completo due rette diagonali separano armonicamente le due rette che dal loro punto di incontro proiettano i vertici del quadrilatero giacenti sulla terza retta diagonale (nel quadrilatero una retta è diagonale quando unisce vertici che non appartengono allo stesso lato).

Riscrivendo il risultato in funzione unicamente delle distanze misurabili sulla piattaforma BDEC si ottiene

cioè la distanza del punto inaccessibile.

Su questo e su altri teoremi simili si basa la misura delle distanze mediante telemetri ottici di vario tipo che rimasero in funzione dalla fine dell'Ottocento fino all'avvento del radar.