Punto_Fisso

Data una circonferenza ed un segmento AB ad esso esterno, se C é un punto della circonferenza si mandino le rette CA e CB che passano per C e per gli estremi A e B del segmento dato. Sia F l'ulteriore intersezione della retta AC con la circonferenza e D l'ulteriore punto di intersezione della retta CB con la circonferenza data. La retta passante per D e parallela ad AB interseca la circonferenza in E e la retta EF taglia la retta AB in P.
Dimostrare che al variare di C sulla circonferenza il punto P resta fisso.

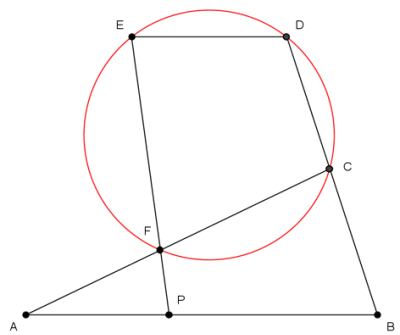
Chiaramente il quadrilatero CDEF è inscritto nella circonferenza assegnata ed è noto che: condizione necessaria e sufficiente affinché un quadrilatero sia inscrivibile in un circonferenza è che gli angoli opposti siano supplementari; quindi per gli angoli interni al quadrilatero si ha

CDE + EFC = FCD + DEF = 180.

E per quanto riguarda gli angoli interni al quadrilatero CFPB risulta

BCF = 180 - FCD = DEF

CFP = 180 - EFC = CDE

e ancora essendo DE parallela ad AB

FPB = 180 - DEF = FCD

PBC = 180 - CDE = EFC

In conclusione gli angoli interni al quadrilatero CFPB sono uguali agli angoli del quadrilatero CDEF e per quanto visto sopra si ha

PBC + CFP = EFC + CDE = 180

BCF + FPB = DEF + FCD = 180

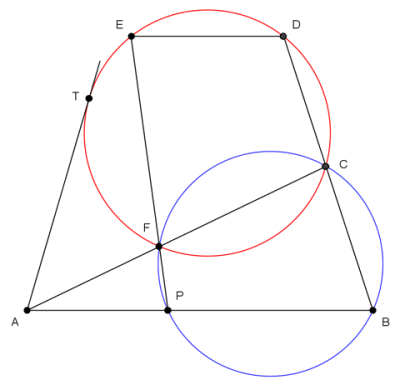
Quindi anche il quadrilatero CFPB è inscrivibile in una circonferenza.

Applicando ora alla circonferenza circoscritta al quadrilatero CFPB il teorema delle due secanti si ha che

AP · AB = AF · AC

Mandiamo ora la retta AT passante per A e tangente alla circonferenza assegnata, applicando di nuovo lo stesso teorema a questa circonferenza otteniamo

AP · AB = AF · AC = AT ²

ma AB e AT sono costanti, quindi indipendenti dalla posizione di C sulla circonferenza data, e allora anche

AP = AT ² / AB

è costante quindi P é un punto fisso sulla retta AB.