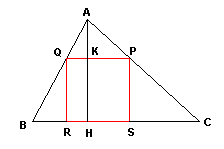
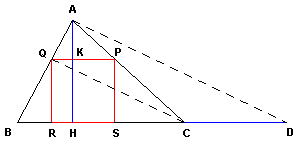
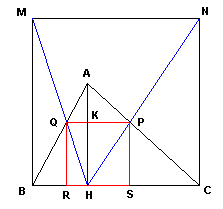
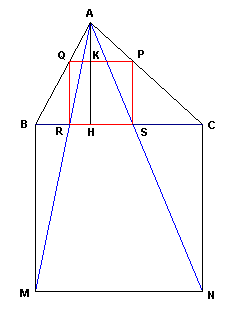
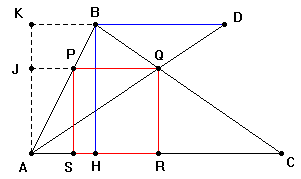
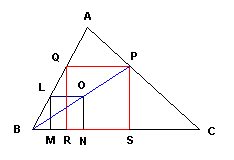
Quadrato inscritto in un triangolo
Diamo una costruzione per individuare il quadrato inscritto con un lato appartenente al lato del triangolo ABC assegnato. La costruzione ci dirà come trovare il quadrato inscritto ma non ci dirà nulla sulla lunghezza del suo lato; a questo provvederemo dopo aver accertato l'esistenza del quadrato in oggetto.
Internamente al triangolo ABC assegnato, tracciamo il quadrato LMNO; la retta passante per B e O taglia il lato AC in P e questo è un vertice del quadrato inscritto. Mandando la parallela ad AC passante per P si ottiene il vertice Q, e dalle perpendicolari a BC si ottengono i restanti vertici R ed S del quadrato inscritto. Infatti per ipotesi LO = ON , inoltre i triangoli BON e BPS sono simili e altrettanto dicasi per i triangoli BOL e BPQ quindi
 

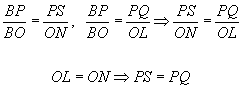
Tracciata l’altezza AH rispetto alla base BC, che interseca PQ in K, dalla similitudine dei triangoli AQP e ABC si ricava

Posto x = PQ = KH, BC = b, AH = h si ottiene

L’ultima soluzione suggerisce una costruzione equivalente che consiste nel prolungare il lato BC di un segmento CD = AH, la parallela ad AD passante per C taglia il lato AB in Q che è un vertice del quadrato inscritto nel triangolo ABC. Infatti i triangoli ABD e QBC risultano simili, quindi le altezze stanno tra loro come le rispettive basi da ciò segue il lato del quadrato inscritto

Le dimostrazioni viste in precedenza possono essere inglobate in un’unica figura e almeno in altri due modi che utilizzano i centri di similitudine.
Dato il triangolo ABC costruiamo il quadro BCNM dalla parte del vertice A. Tracciata l’altezza AH si ha che i segmenti MH e NH tagliano rispettivamente i lati AB e AC nei punti Q e P che sono vertici del quadrato inscritto. Infatti unendo M con H e con N si ottengono 3 coppie di triangoli simili: MHB e QHR, MHN e QHP, NHC e PHS
 

Dato il triangolo ABC costruiamo il quadro BCNM da parte opposta di A. Tracciata l’altezza AH si ha che i segmenti AM e AN tagliano il lato BC rispettivamente in R e S. Dalla similitudine delle coppie di  triangoli: AQR e ABM, ARS e AMN, APS e ACN si ha:
 

Concludiamo con una ulteriore costruzione che per molti aspetti richiama la costruzione presentata all'inizio. Dato il triangolo ABC di altezza BH mandiamo per B un segmento BD = BH, con D da parte opposta di A rispetto all'altezza BH e parallelo alla base AC. Tracciato il segmento AD la sua intersezione Q con BC determina il quadrato PQRS cercato. Consideriamo i due triangoli simili ABD e APQ aventi come altezze KA = BH e JA = PS  , stante la similitudine si ha