E. Lill: radici reali di un polinomio
E. Manet, Exposition universelle 1867, Paris

E. Manet, Exposition universelle 1867, Paris
Nel 1867 un lettore dei "Nouvelles Annales" scrisse alla redazione della rivista francese segnalando un dispositivo in mostra all'esposizione universale di Parigi dello stesso anno. Si trattava di una "macchina" per determinare in modo approssimato le radici reali di un polinomio ideata da un ufficiale dell'esercito austriaco e esposta nel padiglione di quel paese. Lo strumento è segnalato anche nei documenti ufficiali dell'esposizione.

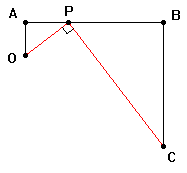
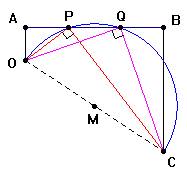
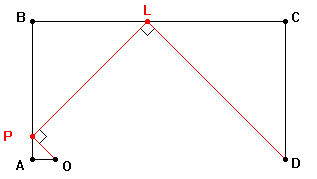
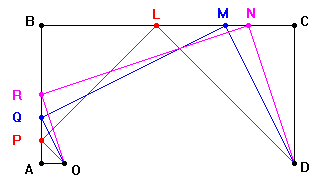
Dalla rivista riprendiamo le costruzioni geometriche alla base del funzionamento dell'apparecchiatura.
 

Rapport sur l'Exposition universelle de 1867, à Paris

 
La costruzione si riferisce ad una equazione contenente un generico polinomio di grado n a coefficienti reali

ma noi faremo soltanto due esempi con polinomi di secondo e terzo grado aventi il coefficiente del termine di grado massimo unitario.
Data l’equazione

si inizia da un generico punto O del piano tracciando un segmento OA di lunghezza 1 che costituirà l’unità di misura per l’intera costruzione. Si traccia un segmento AB di lunghezza AB = p ortogonale a OA che prosegue verso sinistra o verso destra a seconda che il coefficiente del termine di primo grado sia positivo o negativo. Da B si traccia un segmento BC di lunghezza BC = q ortogonale ad AB procedendo verso sinistra o verso destra a seconda che il termine noto abbia lo stesso segno del coefficiente precedente o segno opposto. Fatto ciò se è possibile tracciare un percorso poligonale OPC con P che appartiene ad AB e OP ortogonale a PC allora l’equazione ammette una soluzione reale che è rappresentata dal segmento AP.
Infatti dalla similitudine dei triangoli rettangoli OAP e PBC si ha

Per determinare la seconda radice è sufficiente tracciare una circonferenza avente come centro il punto medio M dei punti O e C e come raggio OM, questa circonferenza taglia AB in P e in Q e il segmento AQ rappresenta la seconda radice reale dell’equazione di secondo grado.
 
La costruzione si ripete identica per una equazione di terzo grado del tipo

e i percorsi che si possono ottenere sono al massimo tre.
Dalla similitudine dei tre triangoli: OAP, PBL, LCD  si ottiene

Il grafico a destra si riferisce all'equazione

le radici sono rappresentate dai segmenti: AP, AQ , AR.