Serie ... geometriche

  
 
 
In questa pagina prenderemo in esame alcune semplici serie di tipo geometrico. Le relative figure geometriche illustreranno la convergenza di queste serie e negli ultimi due esempi anche una possibile applicazione di questi strumenti matematici.
 
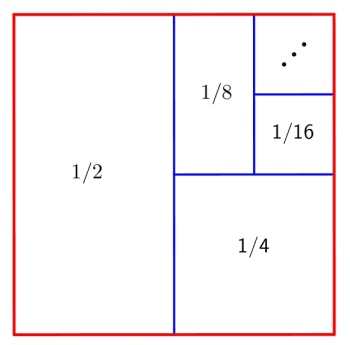
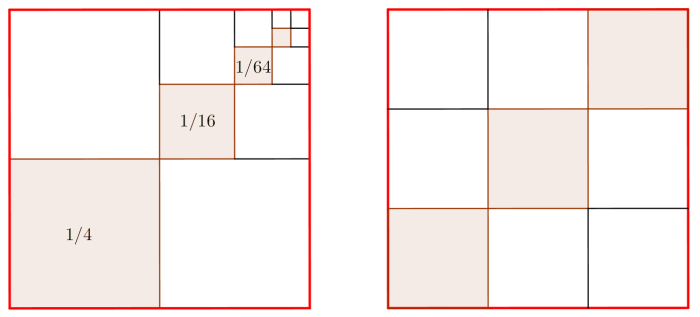
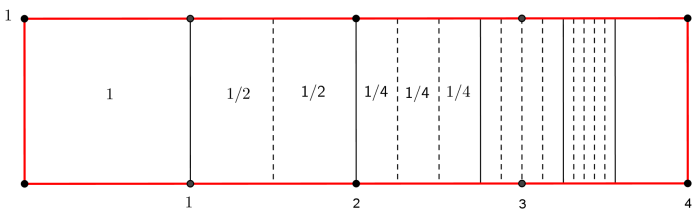
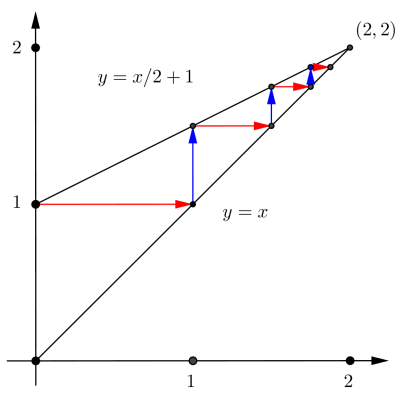
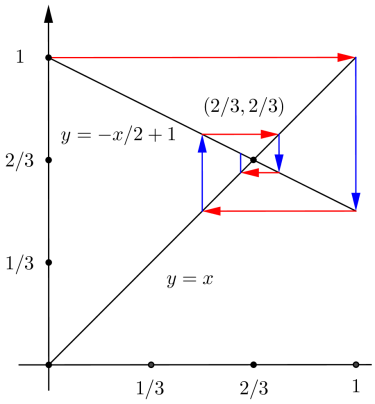
Iniziamo con una serie geometrica la somma parziale di ordine n si può esprimere in forma ricorsiva come

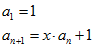o per esteso

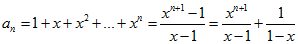da cui segue che

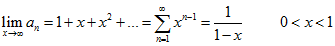La condizione di convergenza è che la ragione sia limitata tra zero e uno perché in questo modo si tiene conto del fatto che questo calcoli verranno applicati a delle figure geometriche in cui tutte le quantità in gioco sono positive o, al più, nulle.
 
 
In figura è rappresentato un quadrato di lato unitario sezionato dimezzandone progressivamente la superficie rimasta. Sommando le aree di tutti i pezzi il risultato deve valere uno. Chiaramente si tratta di una serie geometrica di ragione un mezzo che ha come primo termine il valore un mezzo cioè con la prima potenza della ragione

da cui

Sostituendo ad x il valore un mezzo si ha come risultato l'area unitaria del quadrato di lato unitario.
 
Sotto è riportato un caso simile al precedente dove il quadrato unitario è sezionato prendendo sempre un quarto della superficie rimasta.
 
 
Ancora
da cui

sostituendo ad x il valore un quarto ha come che la somma delle infinite aree è uguale a un terzo dell'area dl quadrato di lato unitario e questa porzione è evidenziata nella figura di destra.
 
Passiamo ora ad una serie che si ricava dalla serie geometrica facendone la derivata prima. In questa sede non ci dilungheremo sulla legittimità di questa operazione ma considereremo questo risultato come valido.
Iniziamo dalle successione delle somme parziali in forma ricorsiva

che per esteso diventa

e mandando il limite si ottiene la somma

In questo caso cercheremo soltanto di illustrare le modalità di convergenza. Utilizzando la ragione x che vale un mezzo si ottiene che la somma infinita converge al valore quattro.
 
 
Nel rettangolo avente i lati di lunghezza uno e quattro cioè di area quattro si vede che i termini che via via si aggiungono sono sempre più piccoli anche se i coefficienti moltiplicativi crescono linearmente seguendo l'ordine del temine considerato. Sappiamo che il valore dei singoli termini che si sommano tenda a zero per n tendente all'infinito è condizione necessaria ma non sufficiente per la convergenza della serie.
 
Passiamo ora a delle possibili applicazioni geometriche per il calcolo della lunghezza di alcuni percorsi di tipo geometrico. Nel primo caso sarà necessario uno dei risultati ottenuti in precedenza e cioè la semplice serie geometrica

 
 
Nella figura riportata sopra ci interessa la somma degli infiniti tratti segnati in rosso e paralleli all'asse delle ascisse. La costruzione è evidente. Da un punto di vista puramente numerico si ha che la successione delle ascisse dei punti dei tratti che ci interessano è la seguente

da cui segue immediatamente che

Per esprimere la lunghezza come somma di più termini basta osservare che

 
 
L'ultimo caso è il più complesso e ci dovremo servire delle somme a segni alterni di cui diamo i caratteri essenziali

Come nel caso precedente e facendo riferimento alla figura che si trova sotto ci interessa la somma delle lunghezze dei tratti in rosso, per quelli in blu la trattazione è la medesima. La costruzione geometrica non richiede spiegazioni particolari.
 
 
 

 

Come nel caso precedente osserviamo la successione numerica delle ascisse dei punti che sono estremi dei tratti rossi

e per comodità separiamo quelli di ordine dispari

da quelli di ordine pari

la successione dei dispari si può esprimere come

mentre quella dei pari

Gli stessi risultati si ottengono assegnando alla ragione x il valore un mezzo nelle serie a segni alterni riportate all'inizio.