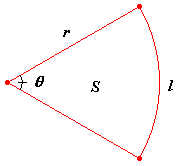
Jakob Steiner

massimi e minimi isoperimetrici
Jakob Steiner (1796 - 1863)
J. Steiner nacque in Svizzera da una famiglia di agricoltori della regione di Berna; fu allievo di Pestalozzi e divenne professore di geometria all'Università di Berlino. Specialista di geometria "sintetica", i suoi lavori si inserirono nello sviluppo della geometria proiettiva e contribuirono al rinnovamento della scuola matematica tedesca.
Da una corposa memoria del 1841 dal titolo "sul massimo e minimo delle figure piane" prendiamo tre teoremi, nelle dimostrazioni seguiremo solo in parte i metodi dell'Autore.

  • Tra tutti i settori circolari isoperimetrici quello avente l'arco pari al diametro ha area massima.
Posti r il raggio della circonferenza, q  l'angolo del settore, l = rq la lunghezza dell'arco e L la lunghezza costante del perimetro si ha
Il settore circolare risulta equivalente alla metà di un triangolo rettangolo avente per cateti il diametro del cerchio 2r e l'arco l = rq  e perimetro costante; tale triangolo è massimo quando è isoscele quindi il settore è massimo quando
In questo caso risulta
Tra tutti i segmenti di cerchio aventi fissata la lunghezza l  dell'arco il semicerchio ha area massima.
Il segmento di cerchio può essere considerato come la metà di una figura che ha come asse di simmetria la corda AB del segmento assegnato ed è noto che tra tutte le figure isoperimetriche piane il cerchio ha area massima, osservato questo la tesi è immediata.
Date due figure di cui sono fissate: la loro forma (cioè sono simili a due figure assegnate) e la somma dei loro perimetri
L =  L1 + L2, si ha che la somma delle loro aree  S = S1 + S2 è minima quando le aree sono proporzionali ai perimetri vale a dire quando  S1 : S2 = L1 : L2 .
Noi ci limiteremo a provare la proposizione nel caso in cui le due figure sono un quadrato e un cerchio. Per fare questo fissiamo come variabili x e y  due rapporti di similitudine che determineranno le dimensioni, ma non la forma, di un quadrato e di un cerchio partendo da un quadrato di lato l , e da un cerchio di raggio r. Quindi
da cui segue
e il minimo si ha quando
In queste condizioni si ha
quindi