Triangolo equilatero di area massima

  
   circoscritto ad un triangolo qualsiasi
 
Dato un triangolo qualsiasi ABC circoscrivere al triangolo dato un triangolo equilatero di area massima.
 
Risolveremo il problema in tre passi. Il primo consiste nel dimostrare un teorema ausiliario.
Mandare per uno dei due punti di intersezione di due circonferenze una corda comune di lunghezza massima.
 
 
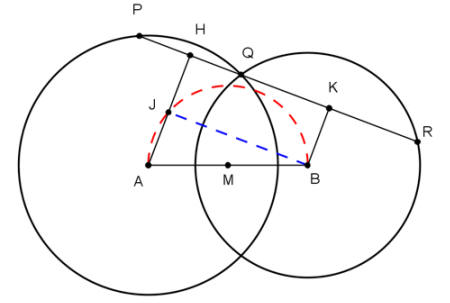
Date due circonferenze di centri A e B sia Q uno dei loro punti di intersezione. Mandiamo per Q la secante comune PR. Dai centri delle circonferenza mandiamo le perpendicolari alle corde PQ e QR, le perpendicolari taglieranno le corde nei loro punti medi H e K: PH = HQ, QK = KR. Se M è il punto medio dei centri A e B delle circonferenza con M come centro tracciamo la semicirconferenza di centro M e raggio AM = MB che interseca una delle perpendicolari alle corde in J.
Nel triangolo rettangolo AJB il cateto JB = HK quindi la lunghezza di JB = PR/2. Variando l'inclinazione della cordaIl il cateto PR cambia anche quella di JB che è parallela a PR e il cateto JB raggiunge la lunghezza massima quando coincide con l'ipotenusa AB del triangolo rettangolo AJB. Allora la corda comune PR, che ha lunghezza doppia di JB, è massima quando è parallela alla retta passante per i centri A e B delle circonferenze date.
Lo stesso problema è stato risolto in modo diverso nella pagina dedicata alle corde di lunghezza massima.
 
Diamo ora una costruzione che, dato un triangolo qualsiasi ABC, ci permetta di ottenere un triangolo equilatero.
Dato un triangolo qualsiasi ABC su ogni lato ed esternamente al triangolo stesso costruiamo un triangolo isoscele avente come base il lato e l'angolo al vertice di 120 gradi. Se AEC, CDB e BFA sono questi triangoli isosceli allora il triangolo EFD è equilatero cioè  EF = FD = DE.
 
 
Convenzionalmente nel triangolo ABC poniamo

inoltre poiché

per gli angoli alla base dei triangoli isosceli si ha

Iniziamo dimostrando che

Applicando il teorema del coseno (Carnot) sui triangoli EAF e FBD risulta

ma

dunque

Inoltre sempre per il teorema del coseno (Carnot) sul triangolo ABC risulta

da cui segue

Per il teorema dei seni

quindi

Procedendo allo stesso modo si dimostra che FD = DE e il triangolo EFD risulta equilatero: EF = FD = DE.
 
Con centri rispettivamente nei vertici del triangolo equilatero EFD tracciamo tre archi di circonferenza che hanno come corde i lati del triangolo ABC  e dai vertici di questo triangolo tracciamo delle corde comuni a due circonferenze consecutive fino a formare il triangolo PQR. Il triangolo PQR è equilatero in quanto equiangolo perché gli angoli ai vertici sono angoli alla circonferenza che insistono su degli archi aventi una angolo al centro 120 gradi (per costruzione).
 
I lati del triangolo equilatero PQR raggiungono il loro massimo quando sono paralleli alle rette passanti per i centri delle circonferenze, cioè quando sono paralleli ai lati del triangolo equilatero DEF. Quando il lati del triangolo equilatero hanno lunghezza massima anche l'area di tale triangolo é massima: