|
Iniziamo
dalla parabola (fig.1). Dati una retta, detta
direttrice, ed un punto
F fuori di essa, detta fuoco, la
perpendicolare per F alla direttrice la incontra in
A e
la retta AF è l'asse della parabola. Il luogo dei punti
P equidistanti dal fuoco e dalla direttrice è una
parabola.
| |
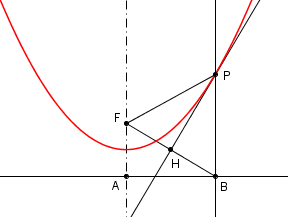
| Sia B un punto
qualsiasi della direttrice (fig.1). L'asse del segmento
FB
taglia in P la perpendicolare in
B alla direttrice.
Il luogo dei punti P che si ottengono al
variare di B sulla direttrice è una parabola.
Dato che i punti appartenenti all'asse di un
segmento sono equidistanti dagli estremi si
ha che il triangolo FPB è isoscele sulla base
FB
e quindi FP =
PB. |
| |
|
|
P1.1
I punti del piano esterni alla parabola sono più vicini alla
direttrice che al fuoco. |
| Sia Q un punto
esterno alla parabola. Mandiamo la retta
QF che
taglia la parabola in P (fig.2). Per i punti
Q e
P mandiamo le perpendicolari in
C e
B alla
direttrice. |
Dalla definizione della
parabola come luogo di punti si ha che FP =
PB. Il
segmento QB è
ipotenusa del triangolo rettangolo QBC e quindi
QC < QB.
Dalla disuguaglianza triangolare nel triangolo
BPQ si ha
QC <
QB < BP +
PQ = FP +
PQ = FQ. |
|
|
|
P1.2
I punti del piano interni alla parabola sono più vicini al fuoco
che alla direttrice. |
|
Sia R un punto interno alla
parabola (fig.2). Tracciamo la retta FR e per
R mandiamo
la perpendicolare in D alla direttrice. |
|
Dalla definizione della
parabola come luogo di punti si ha che FE =
ED e quindi
RD =
RE + ED =
RE + FE.
Dalla disuguaglianza triangolare nel triangolo
FRE si ha
FR <
FE + RE e quindi
FR < RD. |

 1
1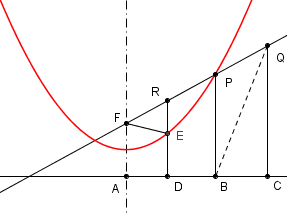 2
2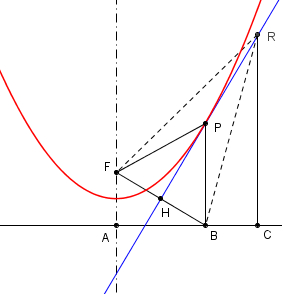 3
3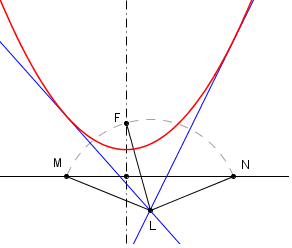 4
4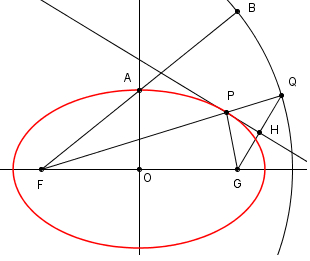 5
5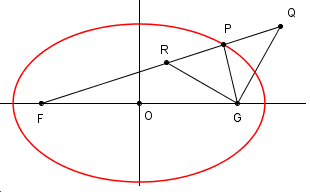 6
6 7
7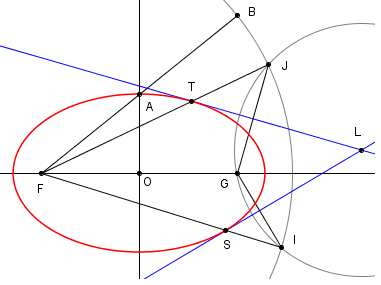 8
8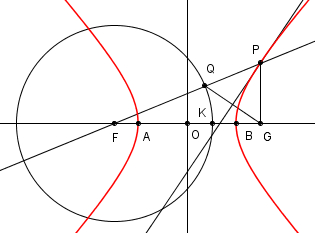 9
9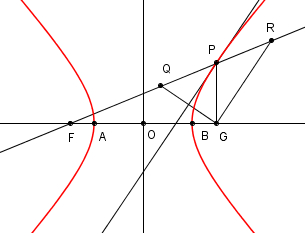 10
10 11
11 12
12