Triangle_Integer

Il libro «Mathematical wrinkles» di Samuel I. Jones (1912) è una raccolta di ricreazioni matematiche, problemi intricati, quesiti d'esame, calcoli sulle unità di misura e tavole numeriche contenenti dati e costanti di vario tipo. Gli argomenti trattati sono molti: algebra, aritmetica, geometria, logica e ci sono anche problemi di calcoli di tipo economico finanziario e di fisica elementare. Se si aggiungono i giochi e i rompicapo l'insieme assume un carattere eclettico. Nel complesso il testo risulta curioso, spesso alla ricerca di "trucchi" e artifici per soluzioni rapide e inattese. Le eccentricità iniziano in copertina dove, su sfondo nero, compare l'antica frase latina dai vari significati esoterici: "Sator arepo tenet opera rotas".

Riportando la frase in cerchio e' evidente il gusto del palindromo ma sfuma quello del quadrato magico che invece si vede bene nell'incisione sulla parete esterna del Duomo di Siena. La frase significa: "Il seminatore, col suo aratro, tiene con cura le ruote." e comunemente viene interpretata come "Dio, dal suo trono, regola con saggezza le sfere (dell'Universo)".
Un esempio del vasto spettro di temi sui quali spazia l'autore si trova nel problema, o forse meglio nel gioco, presentato in forma di filastrocca di cui riportiamo anche la soluzione.

From six you take nine;

And from nine you take ten;

Then from forty take fifty,

And six will remain.

SIX	IX	XL
IX	X	L

S	I	X

Tornando agli aspetti più matematici ci soffermeremo su una tabella, a pagina 306 del testo, che riporta le lunghezze dei lati di 42 triangoli eroniani scaleni. In sostanza si tratta di triangoli scaleni le cui lunghezza dei lati e le aree sono espresse con dei numeri interi. Nelle tabelle in basso sono riportati in nero i lati e le aree dei triangoli presentati nel libro mentre i dati in rosso sono altri 20 triangoli dello stesso tipo che abbiamo aggiunto noi.

n.	a	b	c	S

1	7	15	20	42
2	11	13	20	66
3	13	15	4	24
4	13	15	14	84
5	13	21	20	126
6	13	37	30	180
7	13	37	40	240
8	13	45	40	252
9	13	75	68	390
10	15	35	34	252
11	15	37	26	156
12	15	37	44	264
13	15	41	28	126
14	15	41	52	234
15	17	21	10	84
16	17	25	12	90
17	17	25	26	204
18	17	25	28	210
19	17	39	28	210
20	17	39	44	330
21	17	55	60	462
22	25	29	6	60
23	25	29	36	360
24	25	39	16	120
25	25	39	34	420
26	25	39	40	468
27	25	39	56	420
28	25	51	38	456
29	25	51	52	624
30	25	51	74	300
31	25	63	52	630

n.	a	b	c	S

32	25	63	74	756
33	25	77	74	924
34	29	35	8	84
35	29	35	48	504
36	29	69	52	690
37	35	53	24	336
38	35	53	66	924
39	37	51	20	306
40	37	91	72	1260
41	37	91	96	1680
42	39	41	50	780
43	21	41	50	420
44	39	85	62	1116
45	39	85	92	1656
46	41	51	58	1020
47	41	85	66	1320
48	41	85	84	1680
49	41	85	116	1320
50	51	53	4	90
51	51	53	52	1170
52	51	53	100	714
53	51	55	26	660
54	51	77	40	924
55	61	43	68	1290
56	61	65	14	420
57	61	65	36	1080
58	65	93	34	744
59	69	73	50	1656
60	73	75	52	1800
61	85	91	22	924
62	85	91	48	2016

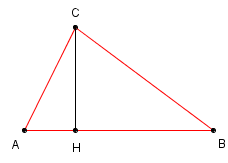
Anche riordinando in modo diverso i dati dei triangoli presentati nel testo non è facile trovare un criterio in base al quale sono generati e scelti. Il modo più semplice per costruire un triangolo eroniano è quello di prendere due triangoli rettangoli i cui lati hanno le lunghezze che formano due terne pitagoriche con due cateti della stessa lunghezza. Unendo i due triangoli mediante i cateti di pari lunghezza si ottiene un triangolo eroniano.

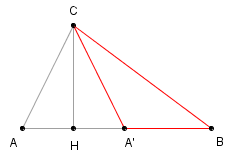
Nella figura riportata sopra il triangolo AHC ha le lunghezze dei lati che sono AH = 20, HC = 15, CA = 25. Nel triangolo CHB si ha CH = 15, HB = 36 e BC = 39. Tutti i lati del triangolo ABC sono interi: AB = AH + HB = 56, BC = 39, CA = 25 e l'area risulta S = 420. Questi triangoli si presentano facilmente a coppie perché se prendiamo il punto A' simmetrico di A rispetto ad H otteniamo il triangolo A'BC che è a sua volta eroniano in quanto CA' = CA = 25, A'B = HB - AH = 16, BC = 39 e l'area vale
S = 120. Aggiungendo i dati in rosso alla tabella abbiamo completato le coppie di questo tipo. Questo modo di costruire triangoli eroniani non è esaustivo perché ne esistono altri in cui tutte le lunghezze delle altezze non sono dei numeri interi; ad esempio il triangolo di lati: 25, 34, 39 e area S = 420. Anche alcuni di questi triangoli sono stati aggiunti alla tabella. I triangoli sono eroniani e, non a caso, è conveniente calcolare la loro area con la nota formula di Erone,

dove p é il semiperimetro, mentre a, b, c sono i lati del triangolo.