Triangoli dimezzati
 
Da un "Cours de mathématiques appliquées" del 1880 di F. Girod e J. T. Canonville, prendiamo in esame alcune costruzioni che consentono di dividere un triangolo in due triangoli equivalenti seguendo una condizione assegnata.
 
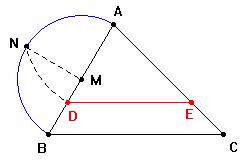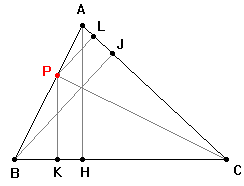
  • Dividere un triangolo ABC in due triangoli equivalenti con una corda  parallela al lato BC.

Sia DE la corda parallela al lato BC che risolve il problema. I triangoli ADE e ABC sono simili e DE dimezza l'area del triangolo ABC quindi
Sia M il punto medio di AB. Tracciata la semicirconferenza di centro M e raggio MA, per M si manda la perpendicolare ad AB che interseca la semicirconferenza in N. Con centro in A si traccia un arco di circonferenza di raggio AN che determina su AB il punto D. La parallela a BC passante per BD determina la corda DE che dimezza il triangolo. Infatti per il secondo Teorema di Euclide si ha

 
  • Dividere un triangolo ABC in due triangoli equivalenti con una corda perpendicolare al lato BC.
Tracciamo l'altezza AH. Se M e' il punto medio di BC allora
S(AMB) = S(AMC) = S(ABC)/2 quindi la corda DE che risolve il problema deve avere l'estremo E appartenere al segmento HC. D'altra parte deve essere S(DEC) = S(AMC) = S(ABC)/2 quindi 

Ma i due triangoli rettangoli AHC e DEC sono simili dunque

e sostituendo nella relazione precedente si ottiene

Sia N il punto tale che MC = CN  e O il punto medio di HN. Con centro in O tracciamo la semicirconferenza di raggio ON e mandiamo la perpendicolare per C al diametro HN che interseca la semicirconferenza in K. Con centro in C tracciamo l'arco di circonferenza di raggio CK che taglia BC in E. La corda ED perpendicolare a BC risolve il problema. Infatti per il secondo Teorema di Euclide risulta

 
  • Dividere un triangolo ABC in due triangoli equivalenti con una corda parallela ad una retta PQ data.
Tracciamo BF parallela a PQ e sia DE la parallela a PQ che risolve il problema, allora

ma i triangoli ADE e ABF sono simili quindi

 
da cui

Sia M il punto medio di AF ed N il suo simmetrico rispetto ad A. Con centro in O, punto medio di NC tracciamo la semicirconferenza di raggio OC. La perpendicolare in A a NC taglia la semicirconferenza in R , con centro in A e raggio AR tracciamo un arco di circonferenza che taglia NC in E. La corda ED parallela a PQ risolve il problema; infatti per il secondo Teorema di Euclide risulta

 
  • Dividere un triangolo ABC in due triangoli equivalenti con una corda avente un estremo P fissato sul lato AB.
Mandate le perpendicolari PK e AH al lato BC supponiamo che sia AH < 2PK (in caso contrario si mandano le perpendicolari ad AD). Tracciamo la parallela a PC passante per A che interseca il prolungamento di BC in D. Se M e' il punto medio di BD allora la corda BM dimezza il triangolo ABC.
Infatti dalla similitudine dei due triangoli  PBC e  ABD si ha

Se M e' punto medio di BD allora 

La dimostrazione precedente si regge sul fatto che M cada internamente al lato BC cioe' che BD < 2BC, vale a dire che  AH < 2PK , ma se questo non accade e' sufficiente mandare le perpendicolari PL e BJ al lato AC e ripetere la costruzione dato che, in questo caso, BJ < 2PL. Infatti

quindi