Triangoli di area massima

  
 
Da un'ampia raccolta di 300 problemi di vario tipo, pubblicata a Parigi nel 1865, del gesuita Ignace-Louis-Alfred Le Cointe (nato a Nimes nel 1823) riprendiamo le soluzioni puramente geometriche di due noti problemi di massimo riguardanti le aree dei triangoli.

«Tra tutti i triangoli aventi la stessa base e lo stesso perimetro determinare quello di area massima.»
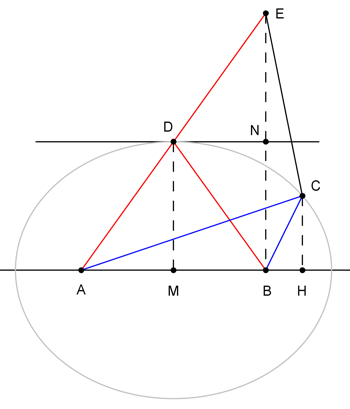
Dato il triangolo ABC consideriamo il triangolo isoscele ABD avente la stessa base AB e lo stesso perimetro quindi

AD = DB,  AD + DB = AC + CB.
Prolunghiamo AD di un segmento DE = AD = DB; il punto D risulta equidistante dai punti A, B ed E quindi il triangolo ABE e' inscrivibile in una semicirconferenza di diametro AE ed ha l'angolo ABE retto. Per la disuguaglianza triangolare si ha

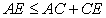ma AE = AD + DB = AC + CB quindi

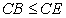Tenuto conto che il triangolo EDB e' isoscele sulla base BE e che l'altezza DN e' parallela alla retta AB  l'ultima disuguaglianza significa che il punto C e' sotto la retta DN quindi la distanza di C dalla retta AB e' minore della distanza del punto D dalla stessa retta. In altri termini l'altezza CH del triangolo ABC e' minore o uguale dell'altezza DM del triangolo ABD ed avendo i due triangoli la stessa base AB risulta

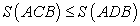Quindi tra tutti i triangoli ABC di base AB e perimetro dato l'isoscele e' quello di area massima.
 

«Tra tutti i triangoli inscrivibili in un cerchio dato quello di area massima č l'equilatero.»

La soluzione proposta dal testo inizia osservando che l'area del triangolo ACB e' massima ha quando il punto C sulla circonferenza e' a distanza massima dalla dalla corda AB. Questo si ha quando C coincide con D ed il triangolo ADB e' isoscele e acutangolo; il triangolo isoscele ottusangolo diametralmente opposto e' un massimo relativo. Dunque se un triangolo inscritto qualsiasi ha due lati di diversa lunghezza esiste sempre un triangolo isoscele inscritto di area maggiore. Allora il triangolo di area massima non puo' avere due lati di diversa lunghezza quindi deve essere equilatero.
A mio avviso la dimostrazione andrebbe modificata per insistere sulla esistenza del massimo. Iniziando con un triangolo inscritto qualsiasi si ottiene un isoscele di area maggiore ed iterando la costruzione si ottiene una successione monotona crescente di aree. Tutti i triangoli sono inscritti in un dato cerchio dunque la successione monotona crescente e' superiormente limitata quindi ammette limite; questo limite e' il massimo dell'area e si ha quando il triangolo inscritto e' equilatero.