 |
|
 |
|
|
|
| La possibilità di dedurre da delle costruzioni geometriche delle identità algebriche utilizzabili nell’aritmetica risale all’antichità. Il pregio di queste costruzioni è quello di racchiudere sinteticamente in una figura le relazioni cercate; può essere un metodo, talvolta suggestivo, utilizzabile per presentare delle identità. Per contro si tratta di un metodo indiretto dove non è sempre facile riconoscere le condizioni aritmetiche nella loro generalità e i limiti del loro impiego. Vediamo alcune di queste costruzioni, le prime tre sono abbastanza note e non richiedono alcun commento. Le ultime tre sono connesse alla possibilità di esprimere dei numeri interi come somme di quadrati. |
|
||
|
||
|
||
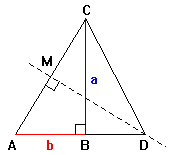
| Disponiamo due segmenti AB e BC ad angolo retto formando il triangolo ABC rettangolo in B con BC = a, AB = b, a > b. Mandiamo l’asse dell’ipotenusa CA che interseca il prolungamento di AB in D. Chiaramente AD = CD e i triangoli rettangoli AMD e ABC sono simili. Applicando il teorema di Pitagora al triangolo CBD si possono ottenere le terne pitagoriche: | |
 |
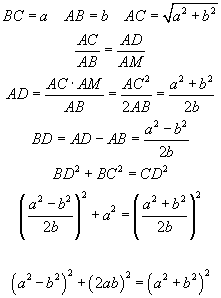 |
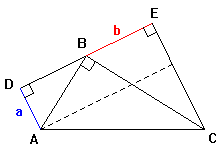
| Dato il triangolo ABC rettangolo in B mandiamo un retta passante per B esterna al triangolo; su questa retta abbassiamo le perpendicolari AD e CE. Chiaramente i triangoli rettangoli ADB e BEC sono simili e ricavando la lunghezza di AC con il teorema di Pitagora si ottiene | |
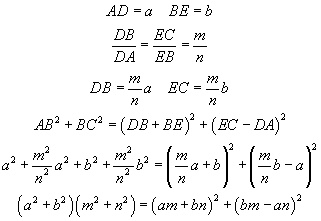 |
 |
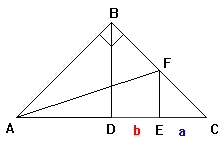
| Dato il segmento DC dividiamolo in due parti: EC = a, DE = b, e sul segmento DC costruiamo il triangolo rettangolo isoscele ABC di ipotenusa AC = 2DC. Sia F un punto del cateto BC. Le perpendicolari mandate da B e da F sulla ipotenusa la intersecano rispettivamente in D e E. Applicando il T. di Pitagora ai triangoli rettangoli ABF e AEF si ottiene | |||||||||||
 |
|
||||||||||