Esercizi di geometria solida
 
  
Sia a un numero reale strettamente positivo e OABC un tetraedro tale che: OAB, OAC e OBC siano dei triangoli rettangoli in O. OA=OB=OC=a. Chiamiamo con I il piede dell'altezza mandata da C nel triangolo ABC, H  il piede dell'altezza mandata da O nel triangolo OIC e con D il punto dello spazio simmetrico di H rispetto ad O.

BAC  2003

  1. Quale è la natura del triangolo ABC ?

  2. Dimostrare che le rette OA e AB sono ortogonali, e che H è l'ortocentro del triangolo ABC.

  3. Calcolare il volume V del tetraedro OABC e l'area S del triangolo ABC.

  4. Esprimere OH in funzione di V e di S e dedurne che OH = a31/2 /3.

  5. Dimostrare che il punto H  ha per coordinate (a/3, a/3, a/3).

  6. Dimostrare che il tetraedro ABCD è regolare (vale a dire che tutti i suoi spigoli hanno la stessa lunghezza).

  7. Sia W il centro della sfera circoscritta al tetraedro ABCD. Dimostrare che W è un punto della retta OH poi calcolarne le coordinate.
  • Chiaramente il triangolo ABC è un triangolo equilatero: AB=BC=CA=a21/2 .
  • Ricordiamo che nello spazio il luogo dei punti equidistanti da tre punti (non allineati) è una retta perpendicolare al piano definito dai tre punti dati. L'origine O è a distanza a da A, B e C quindi la perpendicolare mandata pero O a IC è ortogonale a tutte le rette contenute nel piano definito dai vertici A, B, C del tetraedro dunque anche alla retta AB. Inoltre essendo H un punto del luogo sopra descritto si avrà HA=HB=HC ed H risulta essere circocentro, baricentro e ortocentro del triangolo equilatero ABC.
  • V=(OA×OB×OC )/6=a3/6; S=(AB×CI )/2=a231/2/2. D'altra parte il volume del tetraedro può essere espresso come V=S×OH/3 quindi OH=a31/2/3.
  • Dalla similitudine dei triangoli COI e HKI risulta che HK=OC/3=a/3 e che
    OK=(2/3)OI=a21/2/3 ma OK appartiene alla bisettrice dell'angolo retto xOz quindi
    H(a/3, a/3, a/3).
 
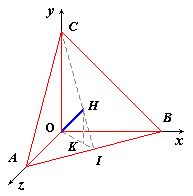
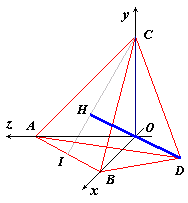
  • I vertici del tetraedro ABCD sono: A(0, 0, a), B(a, 0, 0), C(0, a, 0) e 
    D(-a/3, -a/3, -a/3); applicando la formula della distanza tra punti si ottiene
    AB=BC=CA=AD=BD=CD=a21/2.
  • Il centro della sfera circoscritta al tetraedro ABCD  è equidistante dai suoi vertici quindi appartiene al luogo dei punti equidistanti da A, B, C vale a dire alla retta OH.
    La superficie sferica ha equazione     (x-x0)2 + (y-y0)2 + (z-z0)2  = r2. Imponendo il passaggio per i vertici del tetraedro si ricava x0=y0=z0=a/6 e r = a31/2/2.