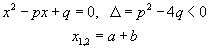lill_radi_imm

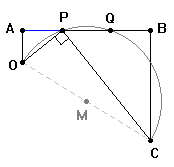
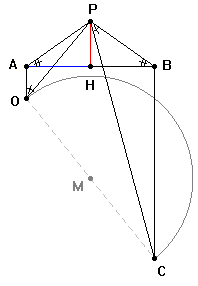
Ritorniamo sui "Nouvelles annales de Mathématiques" del 1868 per trovare un commento della redazione su un lavoro del capitano E. Lill che completa la presentazione del suo metodo grafico per la determinazione delle radici di un polinomio di grado qualsiasi.

Nel 1867 l'Autore aveva presentato il suo metodo per la ricerca delle radici reali sia alla "Exposition universelle" di Parigi che alla "Académie des Sciences" dove compare nei "Comptes réndus" (t.LXV) presentata da Hermite.

Nel 1868, Lill invia uno scritto riguardante il suo metodo grafico all'Accademia Imperiale delle Scienze di Vienna e sugli "Annales" dello stesso anno compare l'estensione del metodo alle radici immaginarie di un polinomio.

Taschenbuch der Militärgeschichte Österreichs

Dai documenti di storia militare dell'impero austriaco risulta che il Capitano Ing. Eduard Lill nato a Brüx [Most, Repubblica Ceca] nel 1830 muore a Görz [Gorizia, Italia] nel 1900.

http://www.wehrgeschichte-salzburg.at/Milchronlogie/Chrono.htm

Anche nel caso delle radici complesse noi ci limiteremo alle equazioni di secondo grado. Per iniziare riprendiamo in breve quanto esposto nella pagina dedicata alla ricerca delle radici reali dell'equazione

Nel percorso OABC avente OA = 1, AB = p e BC = q, il punto P è un punto di AB tale che i triangolo rettangoli OAP e PBC risultano simili. In questo caso posto AP x e detto k il rapporto di similitudine tra i triangoli si ha

Manteniamo il percorso OABC e tutta la notazione del caso precedente: OA = 1, AB = p e BC = q. Nel caso la circonferenza di centro M e raggio MO non tagli il segmento AB allora prendiamo il punto P esterno ad AB ma sempre in modo tale che i triangoli OAP e PBC risultino simili; sia k il rapporto di similitudine tra questi due triangoli.
Chiamiamo AH e PH b OAP e PBC sono simili e ottusangoli quindi si ha

Riprendiamo la tecnica utilizzata nel caso precedente:

Ma il triangolo APH è rettangolo, allora

quindi, riassumendo,

Dato che