Questions and solutions

 
Della rivista mensile "Educational Times" si e' detto in altra sede resta da aggiungere che ogni sei mesi i problemi di matematica, con le rispettive soluzioni, venivano raccolti in un volume dal titolo "Mathematical questions and solutions". Dall'insieme dei problemi proposti e delle soluzioni inviate si nota la partecipazione in maggioranza di inglesi con una presenza significativa di stranieri sia nelle proposte dei testi che nelle soluzioni. Da annate diverse riprendiamo tre quesiti di carattere geometrico.
 
 

 
Iniziamo con il problema geometrico numero 9891 proposto da R. W. Christie.
 
Tracciare una retta che taglia due circonferenze concentriche in modo tale il segmento determinato dalla intersezione della retta con la circonferenza maggiore risulti diviso in tre parti uguali.
 
Seguiremo, in linea di massima, la soluzione data da J. C. St. Clair (Ryder Street, London) nel 1891. Proponiamo due soluzioni di tipo analitico e una costruzione geometrica del tipo "riga e compasso".
 
 

    Sia AL la retta che risolve il problema cioe' tale che AJ = JK = KL = a.
Posti OA = R, OC = r, AJ = a, JK = a/2, OH = x. Per il teorema delle due secanti si ha

    Mandiamo ora la normale ad AL passante per O che dimezza sia la corda AL che la corda JK. Osservato che i due triangoli OHA e OHJ sono entrambi rettangoli in H si ha

   

    Sia D il simmetrico di A rispetto a C. Tracciamo una circonferenza avente per diametro DE; mandata da A la tangente a a questa circonferenza il segmento AT risolve il problema nel senso che se si riporta AK = AT  la retta AK e' tale che
 AJ = JK = KL = a. Infatti DE = 3r – R  quindi    

 
   
Il problema 10568 fu proposto da un francese il prof. Gaston Gohierre de Longchamps mentre la soluzione che ci interessa e' quella di uno spagnolo, un ufficiale del genio, il capitano Ignacio Beyens (5, Calla Santa Ine's, Cadiz)
 
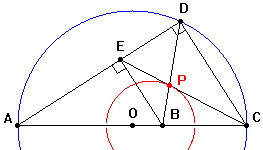
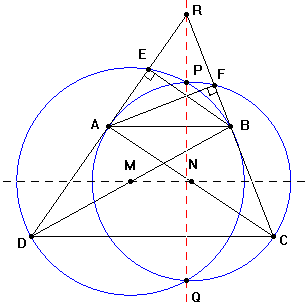
Siano A, B, C tre punti allineati. Per A condurre una retta variabile r e dai punti B e C si abbassino sulla retta r le perpendicolari BE e CD. Trovare il luogo descritto dal punto di intersezione delle diagonali del trapezio rettangolo cosi' formato.
 
Dalla similitudine dei triangoli ABE e ACD si ha
dalla similitudine dei triangoli EPB e DPC si ha
e dalle due similitudini risulta
da cui

ed essendo l'ultimo rapporto una costante il capitano Beyens conclude che il luogo cercato è una circonferenza.

Per entrare nel dettaglio prendiamo il punto D su una circonferenza di raggio OD = r,  poniamo OB = a, fissiamo con k il rapporto costante tra i segmenti BP e BD. Allora
dal triangolo rettangolo OMD si ottiene ,
dalla similitudine dei triangoli BPH e BDM si ha
da cui segue  
 
 
Problema 8362 del 1886. Se su ciascuna delle diagonali di un trapezio prese come diametro si traccia una circonferenza, l'asse radicale delle circonferenze e' ortogonale alle basi del trapezio e passa per il punto di intersezione dei lati obliqui.
 
Soluzioni furono inviate da R. F. Davis, M. A. (Abingdon), e da Ignacio Beyens (Cadice).
Dato che le diagonali sono diametri delle circonferenze i loro centri sono i punti medi delle diagonali vale a dire punti medi di segmenti che hanno gli estremi su due rette parallele, quindi la retta passante per i centri, che e' ortogonale all'asse radicale, e' parallela alle basi del trapezio quindi l'asse radicale e' perpendicolare alle basi del trapezio.
 
Dalla similitudine dei due triangoli rettangoli ERB e ARF risulta

dalla similitudine dei triangoli  ARB e DRC si ha

e dal rapporto di queste due espressioni

.
Per il teorema delle due secanti

da cui

quindi l'asse radicale passa per il punto di intersezione dei lati obliqui.