Tre angoli e tre quadrati

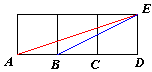
Dati i tre quadrati di figura si tratta di dimostrare, con e senza l'uso della trigonometria, che la somma degli angoli EAD e EBD vale la metà di un angolo retto. Il problema presentato da M. Gardner nel 1970 ebbe come risposta da C.W. Trigg nel 1971 cinquantaquattro dimostrazioni sensibilmente differenti suddivise in quattordici categorie.

Per comodità poniamo gli angoli  EAD=a , EBD=b. Dalla figura si ha immediatamente che tg(a)=1/3 e  tg(b)=1/2 quindi dalla nota relazione tg(a+b)=[tg(a)+tg(b)]/[1-tg(a)tg(b)]  risulta tg(a+b)=1. La somma dei due angoli è minore di due retti quindi vale p/4.

Tracciata la diagonale EC e considerati unitari i lati dei quadrati, dalla figura emerge che EB=√5 ed  EC=√2 , l'area S del triangolo EBC vale 1/2 quindi sin(BEC)=2S/EB·EC=√10/10. Ma anche sin(EAD)=√10/10, ed essendo i due angoli entrambi acuti sono uguali. D'altra parte gli angoli EBD e EFB sono uguali quindi EBD+EAD=FEB+BEC=p/4.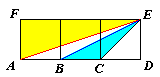

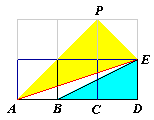Aggiungendo alla figura altri tre quadrati uguali ai precedenti costruiamo il triangolo AEP. Questo triangolo è rettangolo in P e simile al triangolo EBD , infatti i due triangoli hanno i lati in proporzione e il rapporto di similitudine vale AE/BE=AP/BD=EP/ED=√2. Dunque gli angoli PAE ed EBD sono uguali; ne risulta che PAE+EAD=EBD+EAD=p/4.

Aggiungendo alla figura altri tre quadrati unitari uguali ai precedenti costruiamo il triangolo AQE. Il triangolo AQE è isoscele e rettangolo in Q in quanto AQ=QE=√5 e  AE=√10 . Chiaramente i triangoli EBD e CAQ sono uguali quindi anche gli angoli EBD e CAQ sono uguali e ne segue che EAQ=EAC+CAQ=EAC+EBD=p/4.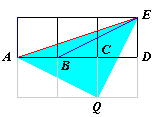