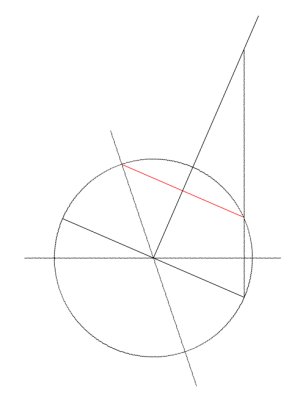Principi di Geometria Fondamentale
di Renato Palmieri
Premessa
Il secondo fronte: la matematica, oggi
Ho a casa, tra i miei libri più cari, una splendida edizione,
in traduzione inglese, delle opere di quattro grandi matematici dell'antichità:
Euclide, Archimede, Apollonio di Perga e Nicomaco di Gerasa. Dopo avervi letto
alcune cose in anni passati, sentii la necessità di seguirne il percorso
nell'interpretazione e nelle analisi conseguenziali dei matematici moderni. Fu
così che, nella stessa veste di profano rispetto a quei geni con la quale mi
ero rivolto alla storia della fisica, scoprii che i matematici moderni avevano
perpetrato un vero e proprio delitto di tradimento nei confronti di quella
meraviglia del pensiero umano, approfittando di un'apparente debolezza di uno
dei più famosi enunciati euclidei: il cosiddetto "quinto postulato"
sulle parallele, che su un piano non s'incontrano.
Naturalmente, la geometria di Euclide - come qualsiasi
geometria (ammesso che ne esista un'altra) - non può non fondarsi su un
certo numero di concetti primitivi, che vengono affermati intuitivamente senza
dimostrazione, proprio perché primitivi, e quel postulato ne è esempio
classico. Ciò non significa che Euclide potesse supporre che un giorno a
qualcuno sarebbe venuto in mente di negarne la verità intuitiva e fattuale, per
costruire castelli pieni di mostruosi "fantasmi matematici", alibi di altrettanto mostruosi "fantasmi fisici", come quelli che
invito a visitare nella voce "Parallele" dell'Enciclopedia
Italiana. Il più terrificante è senza dubbio opera del famoso matematico
Henri Poincaré: "(...) Immaginiamo un mondo tutto racchiuso entro una sfera
(...). Tutti i corpi appartenenti al nostro mondo siano soggetti ad una stessa
legge di dilatazione al variare della temperatura, cosicché questa si potrà
misurare mediante la lunghezza di un corpo qualunque (...)". Il resto
è assolutamente inimmaginabile e sembra davvero una condanna
eccessiva per l'ingenuità del povero Euclide.
Ci si potrà fare un'idea ulteriore dei guasti causati nella
fantasia dei matematici moderni dal rifiuto di quel postulato, leggendo il
capitolo sulla "Geometria non euclidea" nella voce
"Geometria" sempre dell'Enciclopedia Italiana. Il secondo fronte della
battaglia per i
diritti della conoscenza, dopo quello della fisica, si apre perciò sul terreno teoretico della
matematica. Che è quello sul quale si è stabilita nell'età contemporanea
un'alleanza perversa tra due distorsioni complementari, concorrenti in eguale
proporzione ai danni dell'astrattezza
matematica, da un lato, e della concretezza fisica, dall'altro.
Ho già accennato all'inizio che non ritengo si possa dare
ragionevolmente - con una matematica seria - una geometria diversa da quella
euclidea. Pertanto questo non è il trattato sistematico di una nuova geometria. Il mio proposito è solo quello di aggiungere ai
fondamenti di Euclide un
carattere che, dopo di lui, dovrà attendere Archimede per essere introdotto con chiarezza
negli enti matematici: ovvero, l'argomento cinematico. Si vedrà che
questo è, in primo luogo, sufficiente per togliere ogni ragion d'essere ai citati
"fantasmi matematici" e alla loro funzione di supporto per i loro
fratelli fisici. Ma è anche indispensabile per ricavare certe inopinate
conseguenze da una appropriata lettura dei grandi matematici dell'antichità.
Interporrò in corsivo, là dove sia opportuno, al testo dei
principi geometrici veri e propri, numerati progressivamente, alcuni chiarimenti
e puntualizzazioni.
Capitolo I: I "fondamenti"
Una geometria che si definisce
"fondamentale" è tale se i suoi fondamenti sono caratteri
assolutamente primitivi e inconfutabili della specie umana. Naturalmente sarà
sempre possibile che quelli che enunceremo appaiano alla fantasia di
qualcuno non primitivi né inconfutabili. Aggiungo, quindi, semplicemente che la
geometria che trattiamo si rivolge solo a coloro che condividono tale qualità.
1°) Il primo "fondamento" è la percezione,
quanto alla sua origine sensoriale.
2°) Il secondo "fondamento", l'astrazione
(o idealizzazione),
è prerogativa della mente umana: consiste
nello spogliare idealmente da ogni concretezza una percezione, portandola a
limiti assoluti.
Esempio di astrazione da percezione è il concetto di
"punto", che nelle lingue classiche, come ancora in italiano, è
l'idealizzazione di una sensazione di puntura, o del segno di essa (in greco, stigmé
o semeion).
Capitolo II: Gli enti geometrici primi
Si rimanda alla voce citata dell'Enciclopedia Italiana
per la storia dell'evoluzione della geometria nelle diverse epoche. Diamo qui
solo un'idea del terreno insidioso sul quale ci si muove, ricordando che, tra i
vari tentativi fatti da alcuni matematici per trasformare in teorema il V
postulato di Euclide, si risolse in un insuccesso la ridefinizione di rette
parallele da "rette che non s'incontrano" in "rette
equidistanti". Girolamo Saccheri (Sei-Settecento) osservò che una linea
che si definisca come luogo geometrico dei punti equidistanti da una retta data
non è dimostrato che sia essa stessa una "retta".
La geometria fondamentale definisce gli enti geometrici
primi come
risultato dei due fondamenti (cap.I). Gli esempi di percezioni da cui
vengono astratti possono essere vari, e quindi anche diversi da quelli che si danno
appresso.
3°) Il punto è l'astrazione di una percezione
di puntura, o di un segno di penna estremamente piccolo.
Euclide definisce il punto come "ciò che non ha
parti".
4°) La linea è l'astrazione di un filo
sgomitolato.
Euclide la definisce "una lunghezza senza
larghezza".
5°) La retta è l'astrazione d'un filo teso tra
due paletti.
Per Euclide è "una linea che giace egualmente per i
punti su di essa".
6°) Una superficie è l'astrazione dell'esterno
di un corpo.
Euclide la definisce "ciò che ha lunghezza e larghezza
soltanto".
7°) Un piano è l'idealizzazione della
superficie di un tavolo.
L'esempio ci permette di chiarire la genesi degli enti geometrici: Una persona incolta
costruisce un tavolo senza conoscere la teoria geometrica; solo dopo, acculturandosi, lo
astrae fino al concetto di "piano".
Euclide dice che il piano è "una superficie che giace
egualmente per le rette su di essa".
8°) Un volume è l'astrazione dell'interno di un
corpo.
Capitolo III: Gli enti "a priori": Spazio e Tempo
Uso l'insuperabile espressione kantiana come astrazione,
essa stessa, di una percezione.
9°) Lo spazio è idealizzazione della percezione
degli intervalli tra i corpi.
10°) Il tempo è idealizzazione della percezione
del variare degli intervalli tra i corpi, ossia astrazione della percezione del movimento
dei corpi.
Si introduce così nella geometria euclidea l'elemento
"cinematico" che ritroveremo in Archimede. Restano impliciti i
concetti di "misura", con unità convenzionali, dello spazio e del
tempo e quello di "velocità".
Capitolo IV: Gli enti geometrici derivati e le "proprietà"
geometriche
Nel ribadire che questo non è un trattato sistematico della
teoria geometrica, ne tralascerò i dettagli (ad esempio, segmento come parte
di una retta, semiretta, linea aperta, linea chiusa, ecc.), fermandomi solo
sulle definizioni e sui "teoremi" più significativi che conseguono dai principi
suesposti e dall'introduzione del movimento nella geometria.
11°) Angolo piano è la parte di piano percorsa da una
semiretta in rotazione intorno all'origine. Lati dell'angolo sono le
posizioni di partenza e di arrivo della semiretta.
Euclide definisce l'angolo in maniera diversa. La
definizione che se ne dà qui è funzionale al discorso che s'intende fare.
12°) Due angoli sono eguali tra loro, se
percorsi in tempi eguali da una semiretta in rotazione uniforme.
L'angolo è il primo di molti enti geometrici (triangolo,
quadrato, cerchio, ecc), che chiamo "derivati", perché si riconducono
agli otto dei capitoli II e III e non richiedono volta per volta il riferimento ai
due fondamenti (cap.I).
Diamo ora inizio a delle costruzioni geometriche
necessarie a determinare le "proprietà" geometriche degli enti
derivati, sulle quali si fondano i successivi "teoremi" della geometria
fondamentale. Non userò figure disegnate dei procedimenti, invitando i lettori a tradurre graficamente per loro conto la descrizione che
ne farò nel testo.
13°) Siano dati su un piano una retta e un punto fuori
di essa. Tracciamo idealmente da quel punto fino alla retta una serie continua di segmenti
(come per rotazione di una semiretta), poniamo
da sinistra verso destra, rilevandone la lunghezza decrescente fino ad un minimo, oltre il quale essa comincia a crescere.
Chiameremo quel segmento minimo distanza del punto dalla retta.
14°) Si osserva che il primo segmento (sempre da
sinistra) divide il semipiano in due angoli, rispettivamente maggiore e minore.
Procedendo verso destra, a misura che diminuisce la lunghezza del segmento,
l'angolo di sinistra decresce, quello di destra aumenta. Quando quella lunghezza
tocca il minimo (distanza del punto dalla retta), i due angoli diventano eguali;
quindi il primo, continuando a diminuire, diventa minore del secondo, che
continua a crescere.
Nella condizione geometrica del segmento che rappresenta la
distanza del punto dalla retta, i due angoli eguali si dicono retti e il
segmento si dice perpendicolare alla retta. Un angolo maggiore di un
angolo retto è ottuso; se minore, acuto.
15°) L'estremo del segmento perpendicolare che sta
sulla retta si dice proiezione dell'altro sulla retta stessa.
16°) TEOREMA: Per un punto fuori di una retta o in un
punto della retta si può condurre una sola perpendicolare alla retta.
E' dimostrato dal fatto che, per i commi 13°-15°,
un
segmento perpendicolare alla retta per un punto fuori di essa o in un punto di
essa è uno solo.
Capitolo V: Rette parallele
17°) Diciamo parallela ad una retta
data su un piano un'altra retta i cui punti sono tutti equidistanti dalla prima.
18°) TEOREMA: Per un punto fuori di una retta passa una sola parallela,
essendo già provato nella definizione che le due rette non s'incontrano ed
essendo invece da dimostrare che quella definita "parallela" sia
effettivamente una retta, come la retta data. (Vedi succitata critica del
Saccheri, cap.II).
Si tracci un segmento perpendicolare a una retta e si delimiti su questa un segmento comprendente l'estremo del primo. Si muova sul piano il
sistema solidale dei due segmenti, così che il segmento sulla retta segua la
retta stessa. Ne deriva che qualsiasi punto del sistema solidale, ivi compreso
l'altro estremo del segmento perpendicolare, disegnerà sul piano una retta come
quella seguita dal secondo segmento. La linea disegnata da quell'estremo del
primo segmento che non è sulla retta è dunque essa stessa una retta ed è parallela
alla retta data, perché tutti i suoi punti sono da essa equidistanti. E' inoltre
una sola, perché l'estremo del segmento perpendicolare è obbligato ad un solo
percorso: quello vincolato al sistema solidale.
In questo modo, ovvero introducendo nella geometria euclidea
l'aspetto cinematico, che sarà di Archimede, il V postulato di Euclide
si è trasformato in un teorema.
La Quadratura del Cerchio: segue a
"Principi di Geometria Fondamentale", capitoli I-V
Capitolo VI: La geometria del compasso
Quando i matematici moderni parlano del compasso, in realtà
non sanno come funziona, perché non ne hanno riconosciuto la vera descrizione
data da Archimede nella prima delle sue definizioni nel trattato "Sulle
spirali", che è la seguente ed è anche il nostro comma successivo:
19°) Se una retta tracciata su un piano ruota con
velocità uniforme intorno a un estremo, che rimane fisso, e torna continuamente
alla posizione da cui è partita, e se, nello stesso tempo che la retta ruota, un
punto si muove con velocità uniforme lungo la retta cominciando dall'estremo che
rimane fisso, il punto descriverà una spirale nel piano.
Dal momento che i moderni, matematici o fisici che siano,
non hanno occhi per vedere, non si sono accorti che il comunissimo loro compasso
non ha solo un movimento di rotazione, ma ne ha anche un altro lineare di
apertura. Se, invece di far solo ruotare lo strumento per tracciare dei cerchi,
lo avessero usato con entrambi i movimenti a velocità uniforme, si sarebbero
stupiti a "vedere" finalmente sul loro foglio da disegno - invece di un cerchio
- la spirale, appunto, che chiamiamo "di Archimede", e che ha passo costante,
perché il raggio è proporzionale all'angolo di rotazione. La punta esterna del
compasso si muove precisamente lungo una retta nel movimento di apertura e
questa retta ideale ruota con lo strumento, mentre questo continua ad aprirsi.
Abbiamo così trovato il giusto compasso per dimostrare il
teorema del comma che segue, senza nulla di nostro (salvo le peculiarità del
procedimento seguito), ma sulla base esclusiva delle scoperte matematiche del
grande Archimede. Sarà perfettamente inutile tirare in ballo le conclusioni di
Lindemann (1882) sulla trascendenza di pi greco, che riguardano i cerchi
fatti col compasso dei "ciechi" e non la spirale di Archimede. Tuttavia quello
del compasso non è il solo problema, come vedremo tra poco.
20°) TEOREMA: Con l'uso del compasso, come descritto da
Archimede, e di una squadra qualsiasi, è possibile "rettificare" una
circonferenza di raggio dato e quindi, con procedimenti già noti, "quadrare" il
cerchio.
Dopo avere stabilito che il compasso da usare non deve
servire preliminarmente per fare cerchi ma per tracciare una spirale, si entra
su un secondo terreno minato. E' vero, infatti, che Archimede dopo quella
definizione dimostra coi teoremi 18, 19 e 20 che la sua spirale permette di
rettificare la circonferenza (e, ovviamente, noi ci limitiamo qui a richiamare
quei teoremi, già assolutamente dimostrati). Ed è altrettanto vero che i
moderni, pur avendo equivocato sulla funzione del compasso, conoscono senz'altro
la dimostrazione di Archimede, che i lettori troveranno citata e descritta nel
fascicolo dedicato ad Archimede da "LE SCIENZE", nella serie "I grandi della
scienza". Ma sussiste ancora una difficoltà che sembra insuperabile nella fase
della costruzione geometrica, pur effettuato il tracciamento della spirale col
compasso ridefinito: cioè quella di determinare la tangente - indispensabile per
il procedimento - in un punto della spirale, il che Archimede fa solo
teoricamente. Giustamente Pier Daniele Napolitani, autore del fascicolo ora
citato, là dove dice: "Archimede determina la rettificazione della
circonferenza", aggiunge: "o, meglio, riduce il problema della
rettificazione a quello di tracciare la tangente alla spirale". Faccio allora
presente che, per il procedimento particolare che ora descriverò, è sufficiente
tracciare la tangente non in un punto dato della spirale, il che è impossibile
con gli strumenti in causa, ma in uno non predeterminato, il che si può fare,
come vedremo subito.
Si tracci col compasso, così come descritto da Archimede, una
spirale con origine nel polo O. Dopo il primo giro e prima del termine
del secondo ogni raggio della spirale sarà diviso in due segmenti: il minore
all'interno, con estremo nel polo, e il maggiore all'esterno, con estremo sulla
spirale. Il segmento maggiore è il "passo" costante della spirale. Si tracci una
semiretta OH con origine nel polo, che attraversi la spirale tra il primo
e il secondo giro. Si muova la squadra PQR lungo OH da H
verso O fino al punto B di tangenza del cateto PQ con la
spirale (Archimede,"Sulle spirali", teorema 13). Tracciato il raggio
OB, si prolunghi la tangente PBQ fino al punto T di incontro
con la sottotangente, ossia con la perpendicolare ad OB in O. Sul
raggio OB il segmento CB è il passo della spirale. Da C si
conduca la parallela a BT fino all'incontro con la sottotangente in D.
Dai teoremi 18, 19 e 20 di Archimede si dimostra che il
segmento DT è la circonferenza rettificata di raggio OB.
Riportato quindi sulla sottotangente il segmento OV=DT, si tracci il
segmento BV. Sulla semiretta OB sia dato il raggio a piacere di
una circonferenza da rettificare: per esempio, ON. Condotta da N
la parallela a BV fino all'incontro con la sottotangente in M,
sarà OM il segmento che rettifica la circonferenza data, per evidente
legge di proporzionalità. Con procedimenti già noti si passerà quindi a
costruire prima il rettangolo OEFG equivalente al cerchio dato e poi il
quadrato OXYZ di pari area.
Si è così realizzata la visione di Dante nell'ultimo canto
della Divina Commedia, quando si paragona al "geomètra che tutto s'affige / per
misurar lo cerchio, e non ritrova, / pensando, quel principio ond'elli indige".
Dopo sette secoli, il principio è stato ritrovato.
Napoli, 12 novembre 2001
NOTA 1. L'argomento del capitolo VI ha
in comune solo il titolo con l'opera matematica di Lorenzo Mascheroni
(1750-1800), riguardando qui il compasso di Archimede - come detto sopra - e non
quello incompleto dei matematici moderni.

Il compasso dei "ciechi" (i matematici moderni)

Il compasso del Creatore (definito da Archimede)
Biblioteca Nazionale di Vienna, Bibbia del
XIII secolo, da Losapevi dell'arte, Electa Mondadori
NOTA 2. Il compasso normale (il
primo), usato per il solo movimento circolare, non può rettificare la
circonferenza, né - di conseguenza - quadrare il cerchio, così come ha
dimostrato matematicamente Lindemann, e potrebbe stare nelle mani dei Ciechi del
famoso quadro di Brueghel. Il secondo, invece, presenta anche il regolo per
l'apertura lineare, secondo la precisa definizione fatta da Archimede nel
trattato Sulle spirali, e quadra esattamente il cerchio col procedimento
dello stesso Archimede e nostro (comma 20°).
NOTA 3. Il "compasso del Creatore" -
o di Archimede - non è uno strumento solo teorico, utile esclusivamente a
quadrare il cerchio, ma è usato in modo continuo e necessario dalla natura come
guida fisico-geometrica di tutte le strutture circolari, che ruotano
gravitazionalmente con i loro punti di intensità lungo spirali di Archimede (La
Fisica Unigravitazionale e l'Equazione Cosmologica, sez. III, cap. IV a), §§
5 e 12 sgg.; nel libro, pagg. 89 e 98 sgg.). Ne diamo due immagini, relative
rispettivamente alla materia cosiddetta inerte e a quella biologica:

La Fisica e l'Atomo, Le spirali di
crescita su un cristallo di carburo di silicio, Zanichelli editore Bologna

Enciclopedia Italiana, "Dattiloscopia",
Schemi di impronte digitali
NOTA 4. Il comma 20°, in mano a un
lettore addestrato, non richiede una grafica prestampata e graduale per essere
compreso. Allo scopo di facilitare il compito per la generalità dei lettori,
presentiamo appresso solo il risultato finale del procedimento, del quale si
possono seguire nel disegno le tappe successive. Abbiamo scelto ad esempio una
spirale con andamento orario a partire dal polo; riflettendo l'immagine, si avrà
la costruzione antioraria.
Sulla "ignoranza" degli antichi
di Renato Palmieri
In attesa che i matematici nostri contemporanei, ricordandosi
dei loro antichi predecessori, comincino ad arrossire, quando avallano insulsaggini come la "curvatura dello spazio-tempo", o l'
"universo a 11 e fino a 43 dimensioni", o le "regioni di spazio
che contengono meno di nulla", io continuerò ad attingere dagli
antichi certi riferimenti, che andrò proponendo sotto
forma di sfida alla sapienza degli accademici moderni, come ho fatto col breve
trattato sulla geometria. Quanto alla "libertà della fantasia" che,
al di là di tutto, qualcuno rivendica, dichiaro di preferire di gran lunga
quella di Dante Alighieri e di Ludovico Ariosto.
Un campo di divertenti riflessioni mi è offerto dalla
saccenteria con cui si sottolinea, come prova della primitività matematica
all'epoca di Salomone, l'errore che c'è nell'Antico Testamento, là dove si
dice che nel Tempio fu costruita una vasca (il "Mare di Bronzo"), la quale aveva un diametro
di dieci cubiti, un'altezza di cinque e una circonferenza di trenta. Di per sé
la cosa risulta assai strana, perché quegli artefici, assai più che ignorare
l'esatto rapporto tra circonferenza e diametro, mostrano di essere dei goffi
sprovveduti, non accorgendosi che una cordicella di trenta cubiti era
palesemente corta di quasi un cubito e mezzo per misurare il bordo. Ciò in un contesto di istruzioni ricco
di misure significative per l'intero Tempio e per i suoi arredi.
Faccio una sintesi di quanto, in realtà, ho scoperto, essendo
impossibile darne pieno conto in questa sede.
In prima istanza, si riscontra che la sezione della vasca
di 10 per 5 cubiti costituisce il rettangolo da doppio quadrato che genera
notoriamente per costruzione il valore della "sezione aurea" (phi): numero
il quale, come ho dimostrato in tutta la trattazione di fisica, è
al fondamento dell'universo, essendo componente intrinseco dell' "Equazione
Cosmologica".
In secondo luogo, ho scoperto una formula di struttura del vero
pi greco nella quale ricorrono all'infinito in modo sostanziale proprio
quei due numeri (10 e 5), formando un'accoppiata indissolubile.
Come terzo fatto, quella stessa formula di struttura del pi
greco mi si è
rivelata comune alla sezione aurea, salvo un sottraendo sempre eguale che
ricorre all'infinito. (La base comune col pi greco getta luce sulla funzione
teleonomica di phi nell'equazione universale. Nella tradizione, il Mare
di Bronzo è simbolo dell'Oceano cosmico.)
In quarto luogo, da quella formula ho estrapolato un algoritmo
a doppia faccia,
che all'infinito tende da un lato alla sezione aurea (0,618...), avendo
come valore iniziale 0,4 , e dall'altro a pi greco, con valore
iniziale proprio il 3 dell'errore di Hiram, architetto di
Salomone.
E finalmente, l'algoritmo di pi greco non è una
frazione illimitata - come, ad esempio, quella di Wallis -, ma fatta di
numeri interi e segni algebrici, con la presenza del segno di fattoriale (!) e
con n=N tendente a infinito, cioè un numero naturale (1, 2,
3, ...), il cui crescere progressivo approssima sempre di più
nell'algoritmo il valore di pi greco, eguagliandolo all'infinito.
Per divertimento mio e dei lettori, nonché per fornire materia
di furba ironia ai dotti di oggi, ho dato dei nomi simbolici alle
scoperte fatte, traendoli da fonti bibliche. Così, "Mare di Bronzo"
è appunto il nuovo algoritmo di pi greco ora accennato. Quello della
sezione aurea è la "Moltiplicazione dei pani e dei pesci", perché 2
pesci / 5 pani danno il valore iniziale citato di 0,4 e
le successive approssimazioni si ottengono per moltiplicazione infinita.
L'algoritmo a doppia faccia è la "Pietra Angolare" scartata dai
costruttori. Il teorema sulle
parallele del trattato geometrico si denomina "le Croci del Golgota",
appunto perché esse sono tra loro come rette parallele e di più ognuna è il
modello preciso del "sistema solidale" che risolve il problema. Il
teorema, infine, dei commi 19° e 20° di quel trattato è
"il Centurione", per un motivo che vedremo in sede di pubblica
dimostrazione.
Ed ora, a voi, "moderni".
Napoli, 16 novembre 2001
Una curiosa proprietà della spirale di Archimede
di Renato Palmieri
La spirale studiata da Archimede e che porta il suo nome
presenta - come è noto - gli incrementi radiali proporzionali agli angoli
percorsi nella rotazione e per questo ha un "passo" costante, misurato
sui raggi progressivi a partire dal compimento del primo giro. Queste nostre pagine hanno la caratteristica di non
mostrare figure, affidandosi alla personale grafica di ciascun lettore per la
propria comprensione. Disegniamo dunque una retta di base e su di essa un punto
che sia il "polo" della spirale. Dal polo facciamo partire una
spirale, conforme alla regola detta, fermandola al primo giro sulla stessa retta
di base, a 360° dalla partenza. Tracciamo quindi una circonferenza, di raggio
pari a quello della spirale dopo il primo giro.
Ho usato, a questo punto, e immesso in un programma di calcolo
una particolare formula matematica che misura la lunghezza lineare della spirale
in relazione all'angolo di rotazione. Posto il raggio come eguale a 1, la
spirale a un giro dalla partenza risulta misurare 3,383044285. Con la
stessa unità di misura la semicirconferenza vale, ovviamente, 3,1415926535...,
ossia pi greco.
Continuando a disegnare la spirale e fermandoci ad ogni
successivo giro completo, troveremo il raggio del primo giro moltiplicato per il
numero delle rotazioni. Per comodità illustrativa, poniamo che la spirale abbia effettuato
dieci rotazioni: il raggio finale sarà dieci volte quello del primo giro; disegniamo
su esso una circonferenza. Si dovrà ora supporre che tale circonferenza
abbia ruotato su se stessa dieci volte come la spirale e che quindi la misura
della semicirconferenza valga dieci volte pi greco. Posto il raggio della
spirale e della circonferenza a dieci giri come eguale a 1, il calcolo
dà per la lunghezza della spirale rapportata alla semicirconferenza ruotata di
dieci giri il
valore di 3,14583703.
Supponendo di proseguire il calcolo per 100, 1000,
... rotazioni, si evidenzia il fatto che il procedimento tende a raggiungere
all'infinito la misura di pi greco. In altri termini, la spirale di
Archimede tende alla semicirconferenza di pari raggio, ruotata tante volte
quante la spirale stessa. Riporto i calcoli fatti per le potenze di 10
rotazioni, da 0 (1 giro) a 5 (100000 giri), da cui
si vede che già l'ultimo dato coincide con pi greco fino all'ottava
cifra decimale:
100, a 1 giro: 3,383044285
101, a 10 giri: 3,14583703
102, a 100 giri: 3,14165342
103, a 1000 giri: 3,141593444
104, a 10000 giri: 3,141592663
105, a 100000 giri: 3,141592654
Napoli, 29 novembre 2001
La geometria antica e la fondazione di città
di Renato Palmieri
Ogni volta che gli scienziati d'oggigiorno si riferiscono agli
antichi e alle loro conoscenze scientifiche, ne parlano sempre su un presupposto
di primitività, intendendo la scienza come capacità tecnologica e il progresso
come avanzamento sociale. In questo modo non si arriverà mai a capire come mai,
da tempi remoti, la "sezione aurea" sia stata considerata segno del
divino nell'universo, mentre i moderni ci scherzano su come fosse una episodica
curiosità della natura, e solo recentemente la fisica unigravitazionale l'ha
scoperta chiave di volta della totalità delle strutture naturali, ponendola a fondamento di una
"equazione cosmologica" a carattere universale.
Quanto all'avanzamento sociale, se oggi sopravvivesse una
civiltà azteca o druidica, non dovrebbe arrossire per i sacrifici umani fatti
in onore di qualche suo totem divino, viste le moderne carneficine che
spesso si chiamano "umanitarie".
Sorpasserò per adesso la tormentata questione dei valori di phi o di
pi greco connessi alla possibile esatta pendenza della Grande Piramide di
Cheope, oggetto del disinvolto scetticismo di Martin Gardner (LE SCIENZE
n.78, febbraio 1975), per rivelare il contenuto d'un mio personale rilievo circa
l'altra grande piramide, eretta da Chephren, figlio di Cheope. Essa non ha avuto
la ventura di suscitare l'ironia di Martin Gardner, perché le sue proporzioni
sono di una assoluta e incontestabile semplicità e sembrano non poter
nascondere alcun segreto matematico. La sezione di quella piramide è costituita
da un doppio triangolo rettangolo, detto appunto "isiaco" per la sua
provenienza egizia, avente cateti e ipotenusa nel rapporto di 3 (base),
4 (altezza), 5. Le dimensioni che se ne danno nell'Enciclopedia
Italiana sono, infatti, rispettivamente: metri 107,625 (215,25
l'intero lato di base); 143,50; 179,40.
Ora, una piccola sfida all'acutezza dei nostri matematici è la
dimostrazione della seguente proprietà del doppio triangolo isiaco: tracciate
le bisettrici dei due angoli di base e la circonferenza inscritta con centro nel
punto d'incrocio, i due segmenti residui tra vertici e circonferenza sono
ciascuno "sezione aurea" del cateto di base. Veniteci ora a dire che
Chephren non volesse confermare in modo assai semplice le intenzioni geometriche
del padre.
P. S. Dicevano i Latini: Nomen omen (il nome è
presagio). Doveva toccare a un Renato scoprire il segreto di Chephren, dato che
i due nomi hanno lo stesso significato. "Chephren"
nell'Enciclopedia Italiana: "il suo nascere è (quello di) Rie", altra
trascrizione del nome del dio-sole, come Re, Ra. Un pizzico di gioco non
guasta, nelle cose serie...
Napoli, 13 dicembre 2001
1) Neapolis
La chiave astronomica della fondazione di
Neapolis
http://www.webalice.it/catluc1/napoli1.htm
2) Cènabum (Orléans)
L'argomento è legato al teorema dei commi 19° e 20° dei Principi
di Geometria Fondamentale e rinviato, pertanto, allo stesso ambito
dimostrativo.
Una trattazione preliminare se ne fa dopo il successivo
capitolo.
Il teorema dei commi 19° e 20° (CENTVRIO)
Attenzione: La dimostrazione
geometrica del procedimento, che qui è nascosto, è data nel trattato iniziale di
questa pagina (Principi di Geometria Fondamentale).
di Renato Palmieri
§ 1. - Coi primi diciotto commi dei Principi di Geometria
Fondamentale si è dimostrato che l'introduzione del movimento negli enti
geometrici della geometria euclidea porta alla trasformazione in teorema (commi 17°-18°)
del "Quinto postulato" di Euclide sulle parallele.
Due sono i movimenti primitivi introdotti: quello lineare,
di un punto che col suo cammino su un piano disegna appunto una
"linea" (comma 18°), e quello rotatorio, di una
semiretta che percorre intorno all'origine un "angolo" (comma 11°).
L'estremo di un primo segmento della semiretta, opposto all'origine, traccia una linea che
è un "arco" e, a un giro completo, una "circonferenza": il
segmento ne è il "raggio". La superficie di angolo percorsa dal
segmento di semiretta al termine del giro è un "cerchio". Due raggi
posti su una stessa retta ne sono il "diametro".
La geometria del cerchio intesa in senso statico è
inevitabilmente soggetta alla dimostrazione del matematico tedesco Ferdinand von
Lindemann, che nel 1882 diede la prova della trascendenza di pi greco:
tale numero non è radice di alcuna equazione algebrica a coefficienti interi e,
di conseguenza, la circonferenza non può essere rettificata col solo uso
di squadra e compasso, come inutilmente si era tentato di fare per secoli (v.
Enciclopedia Italiana, alla voce "Cerchio").
Il teorema argomento di questa trattazione dimostrerà che,
sviluppata cinematicamente, la geometria del cerchio sfugge completamente
al criterio di Lindemann e comporta in modo teoricamente esatto la
"rettificazione" della circonferenza e, perciò, la mitica
"quadratura del cerchio", con i soli strumenti della squadra e
del compasso voluti dal problema tradizionale.
§ 2. - I capitoli precedenti di questa sezione del sito sono la garanzia preventiva della serietà di quanto ora argomenterò. Stiano perciò
bene attenti i soliti critici per pregiudizio a tenerne conto e a non azzardare
in proposito avventate considerazioni. Sono ben consapevole dell'importanza
della sfida che lancio su questo "secondo fronte" della battaglia per
una nuova scienza: il fronte della matematica pura. I lettori troveranno
un'allusione al discorso di oggi rileggendo la NOTA del 4 aprile (Pasqua) 1999 in
"Programma operativo" della sezione IX, quando citai la
meravigliosa similitudine di Dante nel canto XXXIII del Paradiso: Qual è 'l
geomètra che tutto s'affige / per misurar lo cerchio, e non ritrova, /
pensando, quel principio ond'elli indige, / tal era io a quella vista nova... (che
era la vista di Dio). E' quel "principio" che mi accingo adesso a
svelare, facendone il vero coronamento ideale della mia ricerca de
rerum natura, di cui la matematica è strumento imprescindibile: la
matematica, come precisai nella Premessa di questa sezione, degli antichi
grandi, e non quella degli immemori contemporanei, tanto saccenti quanto - nella
sostanza - "analfabeti".
Mostrerò, in questa sede, i risultati visualizzabili
graficamente e matematicamente del metodo seguito, nascondendone i dettagli
fondamentali, che - come già annunciai nel trattato iniziale - formeranno
oggetto di una pubblica conferenza, correlata al momento (vicino o lontano, non
importa) di un generale riconoscimento tributato alla Fisica Unigravitazionale.
Se ciò non avvenisse, come nelle previsioni ironiche dei neo-tolemaici, la soluzione del problema resterà come quella
scritta a margine dell' "ultimo teorema di Fermat": vi si
arrovelleranno i posteri.
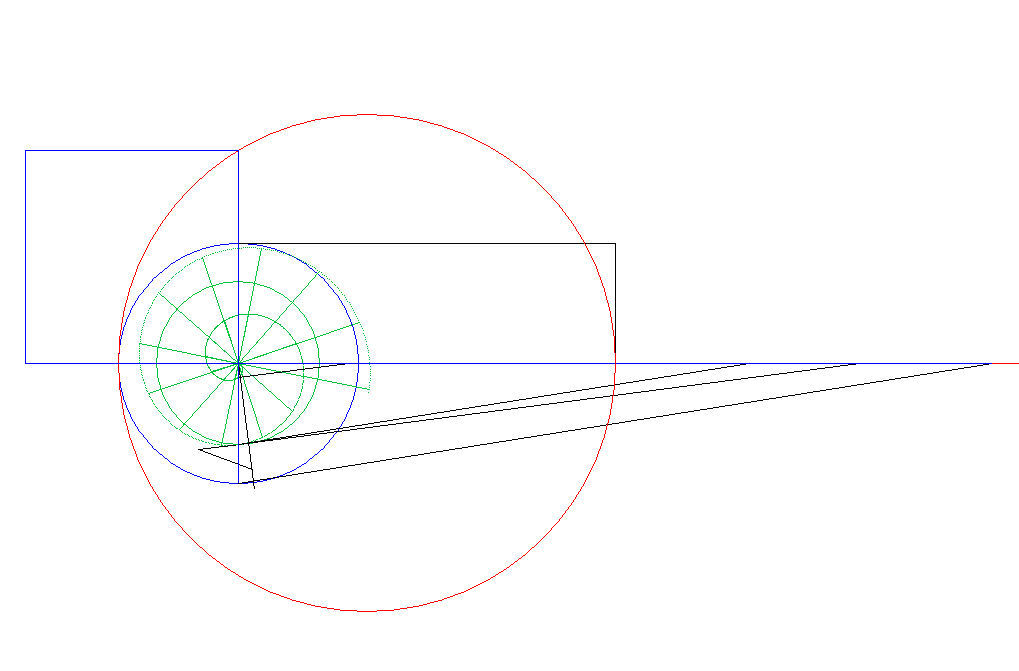
§ 3. - Presenterò ora tre successive schermate di un
programma grafico. In alto si leggono i calcoli che, in base agli input elencati
a sinistra, accompagnano
l'esecuzione, visualizzata solo in parte, del procedimento geometrico
rettificatore. Di questo si manifesta nella prima schermata il primo risultato, consistente
nell'impianto dell'apparato rettificante, che servirà a dare graficamente il
segmento che rettifica una circonferenza di raggio arbitrario, indicato
dall'ultimo input. La seconda schermata si ferma alla rettificazione della
circonferenza, disegnata dall'intero segmento orizzontale che parte dal centro della
circonferenza di raggio voluto, fino al suo estremo. La terza, con procedimenti noti della geometria
corrente, procede alla quadratura del cerchio.
Si badi bene: non sono i calcoli a precostituire il
procedimento geometrico teorico, bensì è questo che viene misurato nel suo
svolgersi da quei calcoli, i quali, solo di conseguenza, determinano il disegno
grafico sullo schermo e confermano visivamente e matematicamente il
procedimento. Se così non fosse, basterebbe disegnare sullo schermo
un cerchio, moltiplicarne il diametro fissato per un valore sempre approssimato
di pi greco e far tracciare al computer un segmento di quella misura, o
applicare altri consimili metodi di carattere elementare o di approssimazione al
problema. Nel caso
nostro, invece, mentre la realizzazione grafica risulta ovviamente imprecisa, come effetto di
strumenti sempre imperfetti, è rigorosamente esatto in assoluto il
risultato teorico, come sottolineato passo dopo passo dai calcoli.
I primi tre input si riferiscono alla parte
nascosta del procedimento e non possono, quindi, essere qui chiariti: ho dato
loro dei valori tali da limitare nello spazio dello schermo il disegno
complessivo. Il quarto e il quinto rappresentano semplicemente le coordinate grafiche del
centro del cerchio da quadrare. L'ultimo è, come si è detto, il valore
assegnato a piacere al raggio della circonferenza da rettificare.
§ 4. - Passiamo ad illustrare più in particolare il
significato degli elementi che emergono dalle tre tappe successive del
procedimento, cui ho dato il nome di CENTVRIO - per un motivo che diremo in
seguito - e che dimostra il teorema del comma 20° così formulato:
Col solo uso del compasso e della squadra, è possibile cinematicamente
, secondo le modalità del comma 19° (che qui si omette per le succitate
ragioni) , "rettificare" una circonferenza di raggio qualsiasi e
quindi, con metodi già noti, "quadrare" il cerchio.
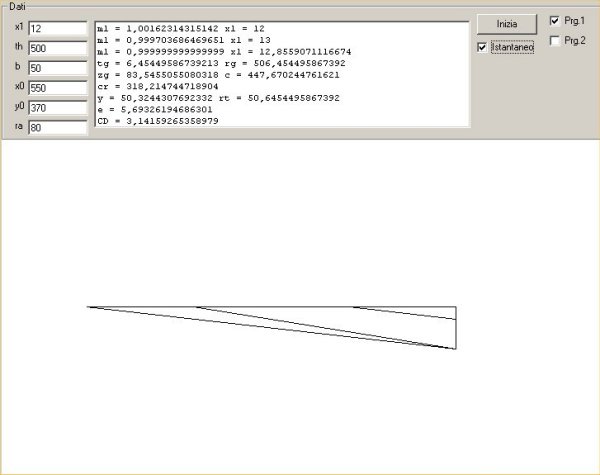
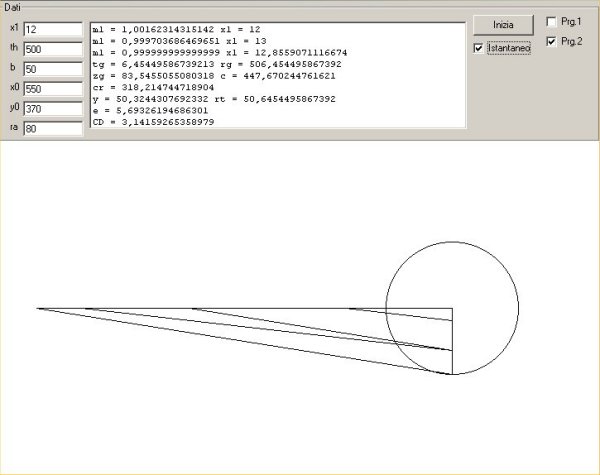
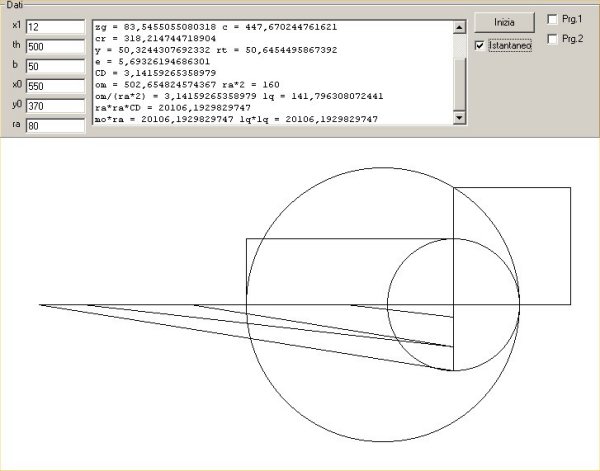
I dati matematici delle prime due schermate si riferiscono alle
operazioni, effettuate con squadra e compasso ma graficamente nascoste, di
costruzione dell'impianto rettificante rappresentato da un triangolo rettangolo
con due linee interne. L'ultimo dato (CD) è il risultato matematico di
quelle operazioni ed è, come si vede, il valore di pi greco, che qui si
mostra esatto fino alla quattordicesima cifra decimale ma che è teoricamente
vero all'infinito, perché il procedimento di rettificazione è corretto in
assoluto.
Nella terza schermata i dati si completano col valore della
circonferenza rettificata in base al metodo seguito e con quelli conseguenti del
rapporto tra essa circonferenza e il diametro dato - cioè di nuovo il vero pi
greco -, il lato del quadrato equivalente e le aree del
cerchio, del rettangolo e del quadrato eguali tra loro. L'arco della
circonferenza grande che insiste sulla somma orizzontale dei due lati del
rettangolo serve a trasformare, secondo un teorema noto, il rettangolo
(che ha la stessa area del cerchio) nel quadrato equivalente.
§ 5. - Il nome CENTVRIO da me dato al teorema si riferisce al
centurione che fa la guardia alla croce di Cristo nella Deposizione di
Benedetto Antelami (un bassorilievo del 1178, nel Duomo di Parma). Il suo scudo
porta circolarmente quella scritta, che ho creduto di interpretare come un misto
anagrammatico di una frase greca: KENTR(ON) EN UIO, ovvero "Il centro nel
Figlio". Mi è parso, cioè, di vedervi un'allusione sacra allo stesso
problema che si porrà Dante: quello della rettificazione in Dio della
circonferenza, dato che l'altezza del centurione è all'incirca pari alla
circonferenza del suo scudo.


Mi piace infine richiamare, con una conclusione curiosa,
proprio la
similitudine dantesca del canto XXXIII del Paradiso, che ho citata nel § 2,
circa il "geomètra che tutto s'affige / per misurar lo cerchio...",
osservando che la presente comunicazione - seppure reticente - sullo stesso
argomento viene pubblicata nel giorno del 33esimo anniversario della nascita
della fisica unigravitazionale, che risale precisamente al 18 marzo del
1969.
Napoli, 18 marzo 2002
I problemi geometrici della tradizione ermetica
di Renato Palmieri
Premessa
Un sentimento duplice mi pervade, quando affronto gli argomenti
di questa sezione matematica. Il primo è una forse non commendevole esaltazione
orgogliosa che mi deriva dall'avere scoperto, a corredo della fisica
unigravitazionale, il vero senso matematico e naturalistico e il sovrasenso
ontologico degli oggetti della mia ricerca nell'ambito della geometria
"tradizionale". Il secondo e contrario è lo stupore quasi vergognoso
di avere appunto solo "scoperto" e non inventato nulla di ciò che la
tradizione umana, nel senso più alto del termine, già mostra di
contenere fin dalla sua storia più remota.
Tanto maggiore è lo sconcerto nel constatare che proprio a
ciò irride il pensiero cosiddetto "scientifico" contemporaneo, quando
confonde la primitività tecnologica degli antichi - per quanto se ne sa - con
una loro presunta ingenuità conoscitiva.
Non indugerò su informazioni, di comune dominio, circa
l'attribuzione di origine neoplatonica a Ermete Trismegisto ("Tre volte
grandissimo") di una incommensurabile sapienza, segreto patrimonio di caste
filosofiche e sacerdotali, con radici fondanti nell'antico Egitto. Osservo
solamente che una tradizione assolutamente concorde dall'antichità ai tempi del
nostro Rinascimento è certa, in primo luogo, dell'unicità e organicità
assoluta delle leggi dell'Universo nell'infinitamente grande come
nell'infinitamente piccolo. In particolare - per il discorso che sto ora
svolgendo -, essa colloca come fondamenti di quelle leggi due rapporti
geometrico-matematici imprescindibili: la "sezione aurea" (vedi Luca
Pacioli, De Divina Proportione, nel Cinquecento) e il rapporto tra
circonferenza e diametro (abbiamo ricordato Benedetto Antelami e Dante, a
proposito della rettificazione della circonferenza).
E' inevitabile che qui prevalga il sentimento di orgoglio
(riproviamolo pure!), quando affermo che queste due assolute verità
naturali e concettuali della tradizione ermetica hanno trovato per la prima
volta solo nella fisica unigravitazionale la loro dimostrazione
rigorosamente razionale e scientifica e nella "equazione cosmologica"
la necessaria quanto evidente traduzione matematica.
Sorge a questo punto l'opportunità di sottolineare una
questione epistemologica di grande importanza. E' quella del rapporto della
nuova fisica e dei suoi principi matematici e naturalistici col triangolo
categoriale rappresentato dalla scienza ufficiale, dalle tendenze cosiddette
"esoteriche" e da quelle "eretiche". La prima - ovvero
l'establishment di tipo accademico e istituzionale - ha, ovviamente, facile
gioco nel condannare le dottrine spesso strampalate dei suoi avversari degli
altri due campi. Ad essa tale situazione offre un alibi importante per fingere
che anche la nuova fisica si debba iscrivere tra i fenomeni di una contestazione fatua e
grossolanamente immotivata. Ma la cartina di tornasole nei confronti di tutte e
tre quelle categorie del triangolo - ivi compresa la scienza accademica - è semplicissima, ed è indicata proprio
dalla tradizione ermetica: un sistema di pensiero che voglia raffrontarsi
conoscitivamente con la natura tutta non può offrire infinite soluzioni
particolari e schizofreniche ai problemi oggetto della sua indagine, ma deve porsi in
un'ottica cosmologicamente unitaria e coerente che comprenda in un solo quadro
"tutto quanto è in basso" così come "tutto quanto è in
alto". Con orgoglio e umiltà contrastanti - come ho prima confessato -
rilevo che solo la nuova fisica possiede questo requisito, ed è anche il solo
sistema teoretico a
denotarlo esplicitamente con la sua stessa denominazione di "unigravitazionale".
L'obliquità dell'eclittica e la fondazione di Cènabum (Orléans)
Risulta spesso piuttosto comico il fatto che, su certi
argomenti e formulazioni delle dottrine "esoteriche", all'irrisione
costante dell'opinione scientifica ufficiale corrisponda oggi un tipo di replica
da parte dei seguaci di quelle, che allude a profonde conoscenze iniziatiche, in
realtà esistenti solo in origine e venute col tempo a scomparire del tutto. E'
il caso dell'oscura massima latina "Visita Interiora Terrae Rectificando
Invenies Occultum Lapidem"("Visita l'interno della Terra:
rettificando, troverai una pietra nascosta"), che si compendia
nell'acrostico VITRIOL. Ne offro ora ai lettori curiosi la mia
interpretazione - per così dire - "geomantica".
Consideriamo nell'esempio geometrico trattato nel precedente
capitolo la variabile indicata con la sigla tg, che ha in quel caso il
valore di circa 6,45. Diciamo ora, senza poterne mostrare il procedimento
genetico (per la reticenza che ci siamo proposta), che essa corrisponde a
un angolo acuto espresso in gradi tra due diametri di un cerchio.
Supponiamo che quel valore sia posto precisamente pari a 23,454680899331,
per un motivo che diremo tra poco: sarebbe allora equivalente a un angolo di
obliquità dell'eclittica di poco superiore a quello attuale, ovvero - il che è
lo stesso - a un'inclinazione dell'asse terrestre rispetto all'asse dell'eclittica di 23° 27'
17", essendo quella dei nostri giorni di 23° 26' 52" (cfr.
la voce "Terra", in astronomia nella EST Mondadori).
Ricordiamo in sintesi che l'obliquità dell'eclittica, e quindi
l'inclinazione dell'asse terrestre, varia in un periodo di
40mila anni all'incirca da un minimo di 21° 55' a un massimo di 24°
20' e che da epoca storica siamo nella fase di diminuzione.
Nella figura seguente si rappresenta un meridiano
terrestre nella situazione del solstizio d'inverno e con il dato di inclinazione dell'asse che abbiamo prima supposto. Il Sole
illumina da sinistra; è mezzogiorno per il semimeridiano di sinistra,
mezzanotte per quello di destra. (Ovviamente, si suppone la Terra come una
sfera geometrica.)
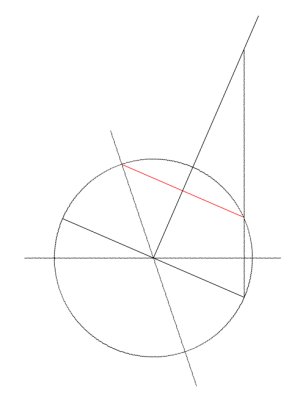
La linea orizzontale è la proiezione del piano dell'eclittica.
Il diametro del cerchio, inclinato su di essa, è proiezione dell'equatore; è disegnato inoltre il
semiasse settentrionale della Terra. Si tracci ora dall'estremo destro del
diametro equatoriale, quello ove è mezzanotte, la perpendicolare al piano dell'eclittica,
prolungandola fino all'incontro col semiasse della Terra: il segmento di questo
che va dal punto d'intersezione al centro della Terra è la rettificazione, col
procedimento riferito nel capitolo precedente, di un arco di meridiano pari a 132,0942912°,
che va dal detto estremo del diametro - passando per il polo Nord - fino a un
parallelo terrestre di latitudine 47,9057088° (supplemento a 180°),
e cioè 47° 54' 21". La corda del cerchio (in rosso) è proiezione del
parallelo. L'estremo dell'arco su quel parallelo avrà il
Sole a mezzogiorno nel solstizio d'inverno.
Segniamo tale estremo nel suolo terrestre con una "pietra
nascosta", che immaginiamo di avervi trovata. Il procedimento ideale
seguito è esattamente quello indicato dalla massima latina: dall'intersezione
tra l'asse terrestre e la perpendicolare all'eclittica siamo penetrati fino al
centro della Terra lungo un segmento rettilineo. Questo rettifica un arco di
meridiano, il cui valore angolare ci ha portati a scoprire la "pietra
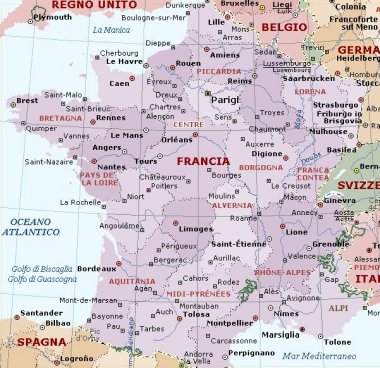
nascosta". Il meridiano è quello che taglia l'antica Gallia dei
Celti, precisamente nel punto dove la Loira volge a sud-ovest con la sua grande
ansa.
Fu lì, nel territorio dei Carnuti, i
"Guardiani della Pietra", che la casta dei Druidi decise di fondare
una nuova città. Nasceva così Cenabum: distrutta da Cesare, fu rifondata
dall'imperatore Aureliano, che la chiamò Aurelianensis urbs, onde il
nome moderno di Orléans (Lat. 47° 55' N).
Ma il fatto che si direbbe prodigioso è che l'angolo
d'inclinazione preso come parametro del nostro discorso, interno ai due limiti
di obliquità dell'eclittica prima indicati e solo per caso prossimo a quello
attuale, non è un dato casuale. Esso è determinato matematicamente, in un
senso che non possiamo qui chiarire, con lo sviluppo iniziale della propagazione
concentrica dei corpi, responsabile negli astri della forma sferoidale e dei
sistemi di anelli presenti in molti di essi, esattamente secondo quanto abbiamo
scritto sulla geometria delle leggi di composizione
ondulatoria nelle sezioni III e IV del sito. Se collochiamo idealmente sul piano
dell'eclittica l'origine della propagazione concentrica generale della Terra, è
come se quel dato di obliquità dell'eclittica ne segnasse geometricamente il
procedere.
Ci risparmino, a questo punto, gli scientisti attuali le
critiche della loro cronologia pseudorazionalistica. Chi è veramente fuori del
tempo, sono soltanto loro. Peccato che non se ne accorgano!
Napoli, 30 maggio 2002
P. S. Le parole conclusive del precedente capitolo sembrano
scritte a postilla dell'opera di un grande saggista e narratore, morto proprio
ieri, 30 maggio: Elémire Zolla. Uno dei suoi saggi si intitola Che cos'è
la tradizione, del 1971. Il pensiero e gli scritti di Zolla sono il monumento
di una battaglia costante contro le pretese dello scientismo contemporaneo, che
sbandiera un'idea di progresso verbalmente "razionalistico", ma in
realtà profondamente conservatore e oscurantista. Dedico al suo ricordo questa
sezione matematica del sito di Fisica Nuova.
Renato Palmieri
Napoli, 31 maggio 2002
SUPPLEMENTO INFORMATIVO: Alcune curiose notizie
pubblicate e commentate in questi giorni di agosto 2004 da due importanti
quotidiani ("la Repubblica" di domenica 8 agosto e "IL MATTINO" di oggi 10
agosto) fanno tornare di immediata attualità questo "secondo fronte" della
nostra polemica scientifica, apertosi su queste pagine il 12 novembre 2001 coi
cinque capitoli iniziali del trattato "Principi di Geometria Fondamentale".
Un intero paginone del primo dei due quotidiani ci racconta
che (occhiello in prima pagina) "Un matematico libanese ha dedicato la vita a
dimostrare il quinto postulato di Euclide": quello delle rette parallele. I
nostri lettori sanno, dai capitoli succitati, che basta aggiungere alla
geometria di Euclide il movimento che vi introduce Archimede, perché il
postulato diventi un teorema, scavando la fossa alle geometrie non euclidee,
delizia dei fisici e dei matematici contemporanei. Dall'articolo di Gabriele
Romagnoli apprendiamo che quello strambo tipo di studioso, di nome Rachid Matta,
perdeva il controllo della macchina "calcolando gli angoli delle curve"; che, se
dorme, si risveglia "dopo tre minuti per l'impellenza di tracciare una
bisettrice" e che ha in questo modo consumato diecimila quaderni e gli ultimi
dieci anni della propria esistenza, per arrivare a una sua "dimostrazione" del
famoso postulato. L'unica cosa che si può assolutamente condividere col prof.
Matta, perché l'abbiamo anche noi espressa chiaramente nella premessa a queste
carte, è la necessità di fare piazza pulita delle moderne fantasie
fisico-matematiche, nate dall'incapacità di leggere correttamente il reale,
applicando ad esso la cristallina chiarezza logica dei grandissimi matematici
dell'antichità. Ha ragione il professore libanese, quando si dice certo che
"senza una geometria logica l'universo è caos, il cielo è vuoto e l'esistenza è
priva di senso".
Ma il comico della vicenda non finisce qui. Contro lo scoop
lanciato da "la Repubblica" si scatena l'ira di Guido Trombetti su "IL MATTINO",
che accusa il collega di non aver chiarito se "si sta scherzando o facendo
satira". "La mia impressione - aggiunge - (per non dire certezza) è che
l'articolo purtroppo tendesse a fare 'divulgazione scientifica'. E se è così,
c'è da restare trasecolati!" La densissima colonna di Trombetti prosegue in una
ortodossa difesa a corpo morto delle geometrie non euclidee, "e cioè quelle
teorie costruite senza il quinto postulato. Che non sono 'meno vere' come
adombrate nell'articolo di cui parlo. Sono solo diverse. (...) Cito per tutte la
relatività che si fonda su una geometria non euclidea".
A proposito della quale egli ricorda in conclusione che "nel
2005 ricorre il centenario della pubblicazione di tre memorie di Einstein che
hanno cambiato la storia dell'umanità". Curiosamente lo stesso giornale aveva
riportato nel numero di venerdì 6 agosto l'accusa mossa ad Einstein dal fisico
teorico Jean Hladik, in un libro pubblicato a Parigi, di avere cioè copiato di
sana pianta da Poincaré la relatività ristretta. Poiché la relatività nel suo
insieme è defunta, senza che lo si sappia ancora in molti, quando nel 1994 cadde
su Giove la cometa Shoemaker-Levy, dimostrando falso il "principio di
equivalenza" con la caduta dei suoi frammenti (i più piccoli per primi), sarebbe
stato auspicabile che almeno egli avesse copiato qualcosa di ragionevole! Quanto
ai docenti di fisica della Federico II e ai loro "eventi" celebrativi, la festa
sarà evidentemente quella della "notte dei morti viventi"... Il giubileo di una
equazione famigerata, per essere stata scritta sulla tolda di una portaerei
americana e per essere solo quella di un grosso botto che costò la vita ad
alcune centinaia di migliaia di persone.