MIKY & GENNY
EQUAZIONI DI GRADO SUPERIORE AL SECONDO RIDUCIBILI ---> INDICE
Vi
sono tipi particolari di equazioni di grado superiore al secondo,
le cui radici si possono trovare risolvendo soltanto equazioni di
secondo grado.
Equazioni biquadratiche
Definizione - Un'equazione si dice biquadratica quando, ridotta a forma normale, è di quarto grado e manca dei termini che contengono le potenze dell'incognita di grado dispari.
Da tale definizione segue che la forma più generale di un'equazione biquadratica, ridotta a forma normale, è del tipo: (1)
ax4+bx2+c=0,
dove a, b, c, sono coefficienti che si suppongono noti, con a≠0.
Se nella (2) si pone :
x2=y,
si ottiene l'equazione: (3)
ay2+by+c=0.
che è di secondo grado nell'incognita y, e si chiama equazione risolvente dell'equazione biquadratica.
Equazioni biquadratiche
Definizione - Un'equazione si dice biquadratica quando, ridotta a forma normale, è di quarto grado e manca dei termini che contengono le potenze dell'incognita di grado dispari.
Da tale definizione segue che la forma più generale di un'equazione biquadratica, ridotta a forma normale, è del tipo: (1)
dove a, b, c, sono coefficienti che si suppongono noti, con a≠0.
Se nella (2) si pone :
si ottiene l'equazione: (3)
ay2+by+c=0.
che è di secondo grado nell'incognita y, e si chiama equazione risolvente dell'equazione biquadratica.
Se l'equazione (3) ammette due radici reali y1 e y2, per la (2), sono soluzioni dell'equazione (1) quei valori della x che soddisfano le due equazioni di secondo grado seguenti: (4)
x2=y1, x2=y2.
Se y1 e y2 sono numeri positivi, le radici delle equazioni (4) sono date rispettivamente da:

e l'equazione biquadratica ammette le seguenti quattro radici:
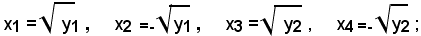
se risulta, y1>0, y2<0, ammette soltanto due radici, date da:

se risulta, y1<0, y2<0, l'equazione data non ammette soluzioni. Se l'equazione risolvente ammette un'unica soluzione y1, allora l'equazione biquadratica ammette due soluzioni, oppure una o nessuna, a seconda che risulti y1>0, y1=0, y1<0.
Se l'equazione risolvente non ammette soluzioni, nemmeno l'equazione biquadratica ammette soluzioni.
Esempi:
1)-risolvere l'equazione:
4x4-37x2+9=0.
L'equazione risolvente è:
4y2-37y+9=0,
ed ammette le radici: y1=9 e y2=1/4.
Si ottengono le soluzioni dell'equazione biquadratica, risolvendo le seguenti due equazioni pure:
x1=3, x2=-3, x3=1/2, x4=-1/2.
Quindi le radici dell'equazione data sono:
x2=9, x2=1/4;
2)-risolvere l'equazione:
5x4-2x2-72=0,
la cui equazione risolvente è:
5y2-2y-72=0,
che ammette le radici: y1=4 e y2=-18/15.L'equazione biquadratica ha quindi due sole radici, date da:
x1=2, x2=-2.
3)-risolvere l'equazione:
x4+13x2+36=0.
L'equazione risolvente è:
y2+13y+36=0,
ed ammette le radici:
Ora, si dovrebbere risolvere le due equazioni:
x2=-4, x2=-9,
ma esse non hanno nessuna radice reale e quindi l'equazione biquadratica data non ammette nessuna soluzione.
Equazioni reciproche
Definizione 1 - Un'equazione a una incognita, ridotta a forma normale, si dice reciproca di prima specie, quando i coefficienti dei termini estremi e di quelli equidistanti dagli stessi estremi sono uguali.
Definizione 2 - Un'equazione a una incognita, ridotta a forma normale, si dice reciproca di seconda specie, quando i coefficienti dei termini estremi e di quelli equidistanti dagli stessi estremi sono opposti.
Esempi di equazioni reciproche:
1)-l'equazione 3x5-7x4+2x3+2x2-7x+3=0 è di prima specie,2)-l'equazione 11x4-8x3+8x-11=0 è di seconda specie.
Nota bene
Si deve osservare che un'equazione reciproca, di grado pari e di seconda specie, deve mancare del termine medio, perchè, essendo esso equidistante dagli estremi, dev'essere uguale al suo opposto. Il nome di reciproche, dato a queste equazioni, deriva dalla seguente proprietà che ci si limita soltanto ad enunciare:
-se un'equazione reciproca ammette per soluzione un dato numero α, essa ammette come soluzione anche il numero reciproco 1/α.
Ad esempio, si consideri la seguente equazione reciproca di terzo grado e di prima specie:
(1) ax3+bx2+bx+a=0
e si supponga che α sia una soluzione di tale equazione, cioè che risulti:
aα3+bα2+bα+a=0.
Dividendo quest'uguaglianza per α3, che è diverso da zero, si ha:

Cioè:
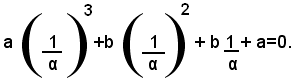
Quest'uguaglianza dimostra che il numero 1/ α, reciproco di α, è una soluzione dell'equazione
Equazioni reciproche di terzo grado
a)-Equazioni di prima specie
Un'equazione reciproca di terzo grado di prima specie, ridotta a forma normale è del tipo: (1)
ax3+bx2+bx+a=0.
Essa si può scrivere sotto la forma:
a(x3+1)+bx(x+1)=0,
e ricordando che:
x3+1=(x+1)(x2-x+1),
si ha:
Si può quindi dire che le soluzioni dell'equazione data (1), sono le soluzioni delle due equazioni:
(x+1)=0, ax2+(b-a)x+a=0.
Dalla prima equazione si ricava x=-1 e si risolve la seconda, che è un'equazione di secondo grado, al solito modo.
Esempi:
1)-risolvere l'equazione:
Se y1 e y2 sono numeri positivi, le radici delle equazioni (4) sono date rispettivamente da:
e l'equazione biquadratica ammette le seguenti quattro radici:
se risulta, y1>0, y2<0, ammette soltanto due radici, date da:
se risulta, y1<0, y2<0, l'equazione data non ammette soluzioni. Se l'equazione risolvente ammette un'unica soluzione y1, allora l'equazione biquadratica ammette due soluzioni, oppure una o nessuna, a seconda che risulti y1>0, y1=0, y1<0.
Se l'equazione risolvente non ammette soluzioni, nemmeno l'equazione biquadratica ammette soluzioni.
Esempi:
1)-risolvere l'equazione:
L'equazione risolvente è:
ed ammette le radici: y1=9 e y2=1/4.
Si ottengono le soluzioni dell'equazione biquadratica, risolvendo le seguenti due equazioni pure:
x1=3, x2=-3, x3=1/2, x4=-1/2.
Quindi le radici dell'equazione data sono:
x2=9, x2=1/4;
2)-risolvere l'equazione:
(x2-3)2+(2x2+1)2=82.
Riducendo l'equazione a forma normale, si ottiene l'equazione biquadratica:
Riducendo l'equazione a forma normale, si ottiene l'equazione biquadratica:
5x4-2x2-72=0,
la cui equazione risolvente è:
5y2-2y-72=0,
che ammette le radici: y1=4 e y2=-18/15.
x1=2, x2=-2.
3)-risolvere l'equazione:
x4+13x2+36=0.
L'equazione risolvente è:
y2+13y+36=0,
ed ammette le radici:
y1=-4 e y2=-9.
Ora, si dovrebbere risolvere le due equazioni:
x2=-4, x2=-9,
ma esse non hanno nessuna radice reale e quindi l'equazione biquadratica data non ammette nessuna soluzione.
Equazioni reciproche
Definizione 1 - Un'equazione a una incognita, ridotta a forma normale, si dice reciproca di prima specie, quando i coefficienti dei termini estremi e di quelli equidistanti dagli stessi estremi sono uguali.
Definizione 2 - Un'equazione a una incognita, ridotta a forma normale, si dice reciproca di seconda specie, quando i coefficienti dei termini estremi e di quelli equidistanti dagli stessi estremi sono opposti.
Esempi di equazioni reciproche:
1)-l'equazione 3x5-7x4+2x3+2x2-7x+3=0 è di prima specie,
Nota bene
Si deve osservare che un'equazione reciproca, di grado pari e di seconda specie, deve mancare del termine medio, perchè, essendo esso equidistante dagli estremi, dev'essere uguale al suo opposto. Il nome di reciproche, dato a queste equazioni, deriva dalla seguente proprietà che ci si limita soltanto ad enunciare:
-se un'equazione reciproca ammette per soluzione un dato numero α, essa ammette come soluzione anche il numero reciproco 1/α.
Ad esempio, si consideri la seguente equazione reciproca di terzo grado e di prima specie:
e si supponga che α sia una soluzione di tale equazione, cioè che risulti:
Dividendo quest'uguaglianza per α3, che è diverso da zero, si ha:

Cioè:
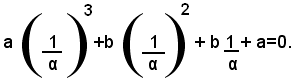
Quest'uguaglianza dimostra che il numero 1/ α, reciproco di α, è una soluzione dell'equazione
(1),
e con ciò si è dimostrato il teorema enunciato, nel caso
particolare delle equazioni reciproche di terzo grado di prima specie.
Equazioni reciproche di terzo grado
a)-Equazioni di prima specie
Un'equazione reciproca di terzo grado di prima specie, ridotta a forma normale è del tipo: (1)
ax3+bx2+bx+a=0.
Essa si può scrivere sotto la forma:
a(x3+1)+bx(x+1)=0,
e ricordando che:
si ha:
a(x+1)(x2-x+1)+bx(x+1)=0,
ossia:
(x+1)[ax2+(b-a)x+a]=0.
ossia:
(x+1)[ax2+(b-a)x+a]=0.
Si può quindi dire che le soluzioni dell'equazione data (1), sono le soluzioni delle due equazioni:
(x+1)=0, ax2+(b-a)x+a=0.
Dalla prima equazione si ricava x=-1 e si risolve la seconda, che è un'equazione di secondo grado, al solito modo.
Esempi:
1)-risolvere l'equazione:
2x3-3x2-3x+2=0.
Essa si può scrivere sotto la forma:
2(x3+1)-3x(x+1)=0,
cioè:
2(x+1)(x2-x+1)-3x(x+1)=0,
(x+1)(2x2-5x+2)=0;
perciò le radici dell'equazione data sono le soluzioni delle due equazioni:
(x+1)=0, 2x2-5x+2=0,
2)-risolvere l'equazione:
3x3+4x2+4x+3=0.
Essa si può scrivere sotto la forma:
3(x3+1)+4x(x+1)=0,
cioè:
3(x+1)(x2-x+1)+4x(x+1)=0,
(x+1)(3x2+x+3)=0;
perciò le radici dell'equazione data sono le soluzioni delle due equazioni:
(x+1)=0, 3x2+x+3=0.
Essa si può scrivere sotto la forma:
2(x3+1)-3x(x+1)=0,
cioè:
2(x+1)(x2-x+1)-3x(x+1)=0,
(x+1)(2x2-5x+2)=0;
perciò le radici dell'equazione data sono le soluzioni delle due equazioni:
(x+1)=0, 2x2-5x+2=0,
che sono:
x1=-1, x2=2, x3=1/2.
2)-risolvere l'equazione:
3x3+4x2+4x+3=0.
Essa si può scrivere sotto la forma:
3(x3+1)+4x(x+1)=0,
cioè:
3(x+1)(x2-x+1)+4x(x+1)=0,
(x+1)(3x2+x+3)=0;
perciò le radici dell'equazione data sono le soluzioni delle due equazioni:
Siccome la seconda di queste due equazioni non ammette soluzioni reali, in quanto il suo discriminante ∆=1-36=-35<0, l'equazione reciproca considerata ammette l'unica soluzione x=-1.
b)-Equazioni di seconda specie
Un'equazione reciproca di terzo grado di seconda specie, ridotta a forma normale, è del tipo: (2)
ax3+bx2-bx-a=0.
Essa si può scrivere sotto la forma:
a(x3-1)+bx(x-1)=0,
e ricordando che:
x3-1=(x-1)(x2+x+1),
si ha:
a(x-1)(x2+x+1)+bx(x-1)=0,
cioè:
a(x-1)(x2+x+1)+bx(x-1)=0,
Si può quindi dire che le soluzioni dell'equazione data (2), sono le soluzioni delle due equazioni:
(x-1)=0, ax2+(a+b)x+a=0.
Essa si può scrivere sotto la forma:
6(x3-1)-19x(x-1)=0,
cioè:
6(x-1)(x2+x+1)-19x(x-1)=0,
(x-1)(6x2-13x+6)=0,
dalla prima equazione si ricava x=1, mentre la seconda ammette per radici 3/2 e 2/3, quindi le radici dell'equazione data sono:
x1=1, x2=3/2, x3=2/3.
Equazioni reciproche di quarto grado
a)-Equazioni di prima specie
Un'equazione reciproca di quarto grado di prima specie, ridotta a forma normale è del tipo: (1)
ax4+bx3+cx2+bx+a=0.
Poichè x=0 non è soluzione dell'equazione, si possono dividere ambo i membri per x2, si ha:
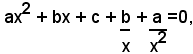
cioè: (2)

Siccome risulta anche:

la (2) si può scrivere sotto la forma: (3)


allora, posto: (4)
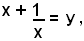
dalla (3) si deduce la seguente equazione di secondo grado:
ay2+by+c-2a=0,
che si chiama equazione risolvente dell'equazione (1). Risolvendo quest'ultima equazione, le sue eventuali radici, sostituite successivamente al posto della y nella (4), permetteranno di calcolare i valori della x che soddisfano l'equazione data.
Esempio: risolvere l'equazione
6x4+5x3-38x2+5x+6=0.
Dividendo ambo i membri per x2, si ha:

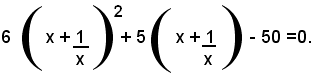
posto: (1)
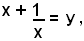
si ottiene l'equazione risolvente:
6y2 + 5y - 50 =0,
le cui soluzioni sono: y1= 5/2, y2 = -10/3. Sostituendo nella (1) al posto della y, prima il valore di y1 e poi quello di y2, si ottengono le equazioni:

ossia:
2x2-5x+2=0, 3x2+10x+3=0.
Risolvendo queste due equazioni di secondo grado, si trovano tutte le radici dell'equazione data, esse sono: x1=2, x2=1/2, x3=-3, x4=-1/3.
b)-Equazioni di seconda speciePerciò si può dire che soddisfano all'equazione (1), i valori della x per cui risulta:
x2-1=0, e ax2+bx+a=0,
Risolvendo queste due equazioni, si ottengono tutte le radici dell'equazione (1).
Esempio: risolvere l'equazione
Questa equazione ammette la soluzione x=1; dividendo il primo membro dell'equazione per x-1, ed uguagliando poi a zero il quoziente, si ha la seguente equazione reciproca, già risolta in precedenza:
6x4+5x3-38x2+5x+6=0.
Perciò le radici dell'equazione data sono: x1=1, x2=2, x3=1/2, x4=-3, x5=-1/3.
Equazioni binomie
Definizione - Un'equazione si dice binomia, quando ridotta a forma normale è del tipo:
(1) axn+b=0.
dove n è un numero intero positivo ed a e b due numeri reali qualsiasi, con a≠0.
Se n=1, l'equazione (1) risulta di primo grado, perchè diventa: ax+b=0.
Se n=2, l'equazione (1) risulta di secondo grado, perchè diventa: ax2+b=0.
In questi due casi la risoluzione è stata vista.
Se n≠1 e n≠2, essendo per ipotesi a≠0, la (1) è equivalente alla: (2)

e la risoluzione di questa equazione equivale all'estrazione della radice ennesima algebrica da un numero reale.
A tal punto, bisogna ricordare, come è stato già visto che,

Per n dispari, l'equazione ammette sempre una ed una sola soluzione.
Esempi:

Equazioni trinomie
Definizione - Un'equazione si dice trinomia, quando ridotta a forma normale è del tipo:
(1) ax2n+bxn+c=0.
dove n è un numero intero positivo ed a≠0.Se n=1, l'equazione (1) risulta di secondo grado, perchè diventa: ax2+bx+c=0,
Se n=2, l'equazione (1) risulta biquadratica, perchè diventa: ax4+bx2+c=0.
ay2+by+c=0,
che si chiama equazione risolvente dell'equazione (1). Risolvendo quest'ultima equazione, le sue eventuali radici, sostituite al posto della y nella (2), permetteranno di calcolare i valori della x che soddisfano l'equazione (1).
Esempi:
1)-risolvere l'equazione trinomia:
8x6-15x3-2=0.
Posto:
x2=y,
si ottiene l'equazione risolvente:
8y2-15y-2=0,
le cui radici sono: y1=2, y2=-1/8.
Si ottengono poi le soluzioni dell'equazione data, risolvendo le seguenti due equazioni binomie: x3=2, x3=-1/8, quindi le radici dell'equazione (1) sono

2)-risolvere l'equazione trinomia:
Posto:
x4=y,
si ottiene l'equazione risolvente:
y2+7y-144=0,
le cui radici sono: y1=9, y2=-16.Si devono ora risolvere le seguenti due equazioni:
x4=9, x4=-16.
La seconda non ammette soluzioni, mentre le radici della prima sono:

L'equazione trinomia data ammette quindi le due radici:

Nota bene
Da tutti gli esempi svolti, si è visto che un'equazione algebrica di grado maggiore di uno, o non ammette nessuna radice, oppure ne ammette un numero che non supera il grado dell'equazione. Ciò si verifica in generale, perchè si può dimostrare il seguente teorema, che ci si limita solo ad enunciarlo:
-nel campo dei numeri reali, un'equazione algebrica di grado n maggiore di uno, o non ammette nessuna radice, oppure ne ammette un numero che non può mai superare il grado n dell'equazione stessa.
b)-Equazioni di seconda specie
Un'equazione reciproca di terzo grado di seconda specie, ridotta a forma normale, è del tipo: (2)
ax3+bx2-bx-a=0.
Essa si può scrivere sotto la forma:
a(x3-1)+bx(x-1)=0,
e ricordando che:
si ha:
a(x-1)(x2+x+1)+bx(x-1)=0,
cioè:
(x-1)[ax2+(a+b)x+a]=0.
Si può quindi dire che le soluzioni dell'equazione data (2), sono le soluzioni delle due equazioni:
Dalla prima equazione si ricava x=1 e si risolve la seconda, che è un'equazione di secondo grado, al solito modo.
Esempio:
1)-risolvere l'equazione:
6x3-19x2+19x-6=0.
Esempio:
1)-risolvere l'equazione:
6x3-19x2+19x-6=0.
Essa si può scrivere sotto la forma:
6(x3-1)-19x(x-1)=0,
cioè:
(x-1)(6x2-13x+6)=0,
dalla prima equazione si ricava x=1, mentre la seconda ammette per radici 3/2 e 2/3, quindi le radici dell'equazione data sono:
Equazioni reciproche di quarto grado
a)-Equazioni di prima specie
Un'equazione reciproca di quarto grado di prima specie, ridotta a forma normale è del tipo: (1)
ax4+bx3+cx2+bx+a=0.
Poichè x=0 non è soluzione dell'equazione, si possono dividere ambo i membri per x2, si ha:
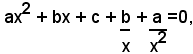
cioè: (2)

Siccome risulta anche:

la (2) si può scrivere sotto la forma: (3)

ossia

allora, posto: (4)
dalla (3) si deduce la seguente equazione di secondo grado:
ay2+by+c-2a=0,
che si chiama equazione risolvente dell'equazione (1). Risolvendo quest'ultima equazione, le sue eventuali radici, sostituite successivamente al posto della y nella (4), permetteranno di calcolare i valori della x che soddisfano l'equazione data.
Esempio: risolvere l'equazione
Dividendo ambo i membri per x2, si ha:

ossia:
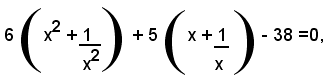
ed anche:
da cui:
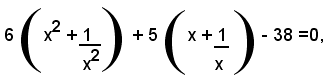
ed anche:

da cui:
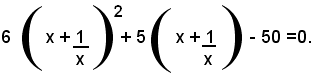
posto: (1)
si ottiene l'equazione risolvente:
le cui soluzioni sono: y1= 5/2, y2 = -10/3. Sostituendo nella (1) al posto della y, prima il valore di y1 e poi quello di y2, si ottengono le equazioni:
ossia:
Risolvendo queste due equazioni di secondo grado, si trovano tutte le radici dell'equazione data, esse sono: x1=2, x2=1/2, x3=-3, x4=-1/3.
b)-Equazioni di seconda specie
Un'equazione reciproca di quarto grado di seconda specie, ridotta a forma normale è del tipo: (1)
ax4+bx3-bx-a=0.
Essa si può scrivere sotto la forma:
a(x4-1)+bx(x2-1)=0,
ossia:
a(x2+1)(x2-1)+bx(x2-1)=0,
cioè:
(x2-1)(ax2+bx+a)=0,
Essa si può scrivere sotto la forma:
ossia:
cioè:
(x2-1)(ax2+bx+a)=0,
Risolvendo queste due equazioni, si ottengono tutte le radici dell'equazione (1).
Esempio: risolvere l'equazione
5x4-26x3+26x-5=0.
Si ha:
5(x4-1)-26x(x2-1)=0,
5(x2+1)(x2-1)-26x(x2-1)=0,
(x2-1)(5x2-26x+5)=0.
Tale equazione è equivalente alle due equazioni di secondo grado seguenti:
(x2-1)=0, (5x2-26x+5)=0,
che, risolte, ammettono come radici:
Equazioni reciproche di quinto grado
Si può dimostrare facilmente che ogni equazione reciproca di quinto grado di prima specie, ammette sempre la radice -1, mentre ogni equazione reciproca di quinto grado e di seconda specie, ammette sempre la radice +1. Perciò il rispettivo primo membro, per il teorema di Ruffini, è divisibile, nel primo caso per -1 e nel secondo per +1. L'equazione si scompone quindi in un'equazione di primo grado e in un'equazione reciproca di quarto grado.
Esempio: risolvere l'equazione reciproca di seconda specie
6x5-x4-43x3+43x2+x-6=0.
Si ha:
Tale equazione è equivalente alle due equazioni di secondo grado seguenti:
che, risolte, ammettono come radici:
x1=1, x2=-1, x3=5, x4=1/5.
Equazioni reciproche di quinto grado
Si può dimostrare facilmente che ogni equazione reciproca di quinto grado di prima specie, ammette sempre la radice -1, mentre ogni equazione reciproca di quinto grado e di seconda specie, ammette sempre la radice +1. Perciò il rispettivo primo membro, per il teorema di Ruffini, è divisibile, nel primo caso per -1 e nel secondo per +1. L'equazione si scompone quindi in un'equazione di primo grado e in un'equazione reciproca di quarto grado.
Esempio: risolvere l'equazione reciproca di seconda specie
Questa equazione ammette la soluzione x=1; dividendo il primo membro dell'equazione per x-1, ed uguagliando poi a zero il quoziente, si ha la seguente equazione reciproca, già risolta in precedenza:
6x4+5x3-38x2+5x+6=0.
Perciò le radici dell'equazione data sono: x1=1, x2=2, x3=1/2, x4=-3, x5=-1/3.
Equazioni binomie
Definizione - Un'equazione si dice binomia, quando ridotta a forma normale è del tipo:
(1) axn+b=0.
dove n è un numero intero positivo ed a e b due numeri reali qualsiasi, con a≠0.
Se n=1, l'equazione (1) risulta di primo grado, perchè diventa: ax+b=0.
Se n=2, l'equazione (1) risulta di secondo grado, perchè diventa: ax2+b=0.
In questi due casi la risoluzione è stata vista.
Se n≠1 e n≠2, essendo per ipotesi a≠0, la (1) è equivalente alla: (2)

e la risoluzione di questa equazione equivale all'estrazione della radice ennesima algebrica da un numero reale.
A tal punto, bisogna ricordare, come è stato già visto che,

Per n dispari, l'equazione ammette sempre una ed una sola soluzione.
Esempi:

Equazioni trinomie
Definizione - Un'equazione si dice trinomia, quando ridotta a forma normale è del tipo:
dove n è un numero intero positivo ed a≠0.
Se n=2, l'equazione (1) risulta biquadratica, perchè diventa: ax4+bx2+c=0.
In questi due casi la risoluzione è stata vista.
Supposto n>2, e posto (2) xn=y, dalla (1) si deduce l'equazione di secondo grado in y:
che si chiama equazione risolvente dell'equazione (1). Risolvendo quest'ultima equazione, le sue eventuali radici, sostituite al posto della y nella (2), permetteranno di calcolare i valori della x che soddisfano l'equazione (1).
Esempi:
1)-risolvere l'equazione trinomia:
Posto:
si ottiene l'equazione risolvente:
8y2-15y-2=0,
le cui radici sono: y1=2, y2=-1/8.
Si ottengono poi le soluzioni dell'equazione data, risolvendo le seguenti due equazioni binomie: x3=2, x3=-1/8, quindi le radici dell'equazione (1) sono

2)-risolvere l'equazione trinomia:
x8+7x4-144=0.
Posto:
si ottiene l'equazione risolvente:
le cui radici sono: y1=9, y2=-16.Si devono ora risolvere le seguenti due equazioni:
x4=9, x4=-16.
La seconda non ammette soluzioni, mentre le radici della prima sono:

L'equazione trinomia data ammette quindi le due radici:
Nota bene
Da tutti gli esempi svolti, si è visto che un'equazione algebrica di grado maggiore di uno, o non ammette nessuna radice, oppure ne ammette un numero che non supera il grado dell'equazione. Ciò si verifica in generale, perchè si può dimostrare il seguente teorema, che ci si limita solo ad enunciarlo:
-nel campo dei numeri reali, un'equazione algebrica di grado n maggiore di uno, o non ammette nessuna radice, oppure ne ammette un numero che non può mai superare il grado n dell'equazione stessa.