MIKY & GENNY
FRAZIONI ALGEBRICHE ---> INDICE
Definizione - Si chiama frazione algebrica il quoziente di due polinomi, il secondo dei quali non nullo.
Si deve ricordare che un polinomio può avere anche un solo termine, cioè ridursi ad un monomio.
Ad esempio, sono frazioni algebriche, le seguenti espressioni:

I due polinomi, di cui la frazione algebrica indica il quoziente, si chiamano termini della frazione, e precisamente, il polinomio che va assunto come dividendo si dice numeratore, mentre il polinomio che va assunto come divisore dicesi denominatore.
Anche un polinomio qualsiasi può considerarsi frazione algebrica, quando al denominatore si assegna valore uno.
Una frazione algebrica ha significato per tutti i valori delle lettere che vi compaiono, eccetto per quei particolari valori che rendono nullo il denominatore.
Infatti, secondo la definizione data, una frazione algebrica è un quoziente, e questo esiste solo se il divisore è diverso da zero.
Esempi:
1)-la frazione:

non ha significato per a=1 e per a=-1, perchè per tali valori risulta a2-1=0.
2)-la frazione:

e quindi, poichè i due termini della frazione hanno in comune il fattore 2a+b, si possono dividere per il suddetto fattore entrambi i termini della frazione, ottenendo:
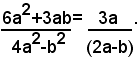
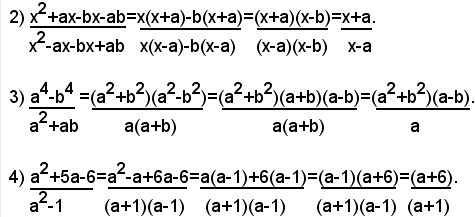
Riduzione di frazioni algebriche allo stesso denominatore
Siccome una frazione algebrica non cambia valore se si moltiplicano entrambi i termini per una stessa espressione non nulla, allora due o più frazioni si possono sempre ridurre allo stesso denominatore. Ad esempio, le due frazioni:
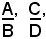
si possono sempre ridurre allo stesso denominatore, moltiplicando entrambi i termini della prima per il denominatore della seconda, ed entrambi i termini della seconda per il denominatore della prima. Si ottengono così le due frazioni equivalenti alle date:

Resta inteso che in pratica, talvolta è necessario prendere come denominatore comune delle frazioni un'espressione più semplice di quella data dal prodotto dei denominatori delle singole frazioni. Ad esempio, se i denominatori delle frazioni sono dei monomi, conviene prendere come denominatore comune il loro m. c. m.
Esempio: ridurre allo stesso denomonatore le seguenti frazioni:
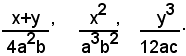

Se poi i denominatori delle frazioni, che si vogliono ridurre allo stesso denominatore, sono polinomi, allora si cerca anzitutto di trasformare in prodotto questi polinomi. Dopo di che si prende come denominatore comune il prodotto di tutti i fattori comuni e non comuni, che compaiono in questi prodotti, preso ciascuno una sola volta e con il maggiore degli esponenti, che esso ha nei vari denominatori.
Esempi:
1)-ridurre allo stesso denominatore le seguenti frazioni:
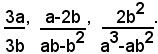
I denominatori delle frazioni, scomposti in prodotto, sono: 3b, b(b-a), a(a+b)(a-b). Si vede allora che si può assumere come denominatore comune il prodotto: 3ab(a+b)(a-b). Dividendo il denominatore comune per i denominatori delle singole frazioni, si ottengono rispettivamente i seguenti quozienti: a(a+b)(a-b), 3a(a+b), 3b; quindi le frazioni equivalenti alle date, e ridotte allo stesso denominatore, sono:

2)-ridurre allo stesso denominatore le seguenti frazioni:

I denominatori delle frazioni, scomposti in prodotto, sono: x(x+y), (x+y)(x-y), (x+y)2, e perciò come denominatore comune si prende: x(x-y)(x+y)2; quindi le frazioni ridotte allo stesso denominatore sono:

due frazioni algebriche aventi lo stesso denominatore, per definizione di quoziente si ha:

da cui, sommando membro a membro:

ossia, per l'inversa della proprietà distributiva della moltiplicazione, risulta:

Ma questa uguaglianza esprime che la somma

Si può enunciare la seguente regola:
-per calcolare la somma algebrica di due o più frazioni, prima si riducono allo stesso denominatore, e poi la somma è data da quella frazione algebrica che ha per numeratore la somma algebrica dei nuovi numeratori e come denominatore il denominatore comune scelto per le frazioni date.
Naturalmente, dopo aver trovato la frazione somma, conviene, se è possibile, semplificarla.
Si deve ricordare che un polinomio può avere anche un solo termine, cioè ridursi ad un monomio.
Ad esempio, sono frazioni algebriche, le seguenti espressioni:

I due polinomi, di cui la frazione algebrica indica il quoziente, si chiamano termini della frazione, e precisamente, il polinomio che va assunto come dividendo si dice numeratore, mentre il polinomio che va assunto come divisore dicesi denominatore.
Anche un polinomio qualsiasi può considerarsi frazione algebrica, quando al denominatore si assegna valore uno.
Una frazione algebrica ha significato per tutti i valori delle lettere che vi compaiono, eccetto per quei particolari valori che rendono nullo il denominatore.
Infatti, secondo la definizione data, una frazione algebrica è un quoziente, e questo esiste solo se il divisore è diverso da zero.
Esempi:
1)-la frazione:

non ha significato per a=1 e per a=-1, perchè per tali valori risulta a2-1=0.
2)-la frazione:

non ha significato per a=b.
Quindi: nelle frazioni algebriche vanno esclusi, per le lettere che compaiono nei denominatori, quei valori numerici per i quali tali denominatori si annullano.
Nota bene
Mentre in aritmetica i termini di una frazione erano sempre numeri interi assoluti, nelle frazioni algebriche il valore che ciascuno dei due termini assume, dipende dai valori che si attribuiscono alle lettere in essi contenute, e può, a seconda dei casi, risultare un numero relativo intero o fratto. Nonostante ciò, per il calcolo delle frazioni algebriche valgono le stesse regole viste per le frazioni aritmetiche.
Definizione - Due frazioni algebriche si dicono equivalenti quando assumono valori numerici uguali, qualunque sia il valore attibuito alle lettere, esclusi quelli per i quali almeno una delle due frazioni perde significato.
Da tale definizione, si nota che il concetto di equivalenza di due frazioni prescinde da quei particolari valori che attribuiti alle lettere fanno perdere il significato ad almeno una frazione. In altri termini, due frazioni per essere equivalenti, non devono essere uguali per tutti i possibili valori che si possono attibuire alle lettere, ma soltanto per quei valori che non fanno perdere significato a nessuna delle due frazioni.
Semplificazione delle frazioni algebriche
Per comprendere le proprietà delle frazioni algebriche, bisogna ricordare che una frazione algebrica indica semplicemente il quoziente fra il numeratore ed il denominatore. Perciò, se si indica A/B una frazione algebrica, per definizione di quoziente, si ha:



Scomponendo numeratore e denominatore in fattori, si ha:

Quindi: nelle frazioni algebriche vanno esclusi, per le lettere che compaiono nei denominatori, quei valori numerici per i quali tali denominatori si annullano.
Nota bene
Mentre in aritmetica i termini di una frazione erano sempre numeri interi assoluti, nelle frazioni algebriche il valore che ciascuno dei due termini assume, dipende dai valori che si attribuiscono alle lettere in essi contenute, e può, a seconda dei casi, risultare un numero relativo intero o fratto. Nonostante ciò, per il calcolo delle frazioni algebriche valgono le stesse regole viste per le frazioni aritmetiche.
Definizione - Due frazioni algebriche si dicono equivalenti quando assumono valori numerici uguali, qualunque sia il valore attibuito alle lettere, esclusi quelli per i quali almeno una delle due frazioni perde significato.
Da tale definizione, si nota che il concetto di equivalenza di due frazioni prescinde da quei particolari valori che attribuiti alle lettere fanno perdere il significato ad almeno una frazione. In altri termini, due frazioni per essere equivalenti, non devono essere uguali per tutti i possibili valori che si possono attibuire alle lettere, ma soltanto per quei valori che non fanno perdere significato a nessuna delle due frazioni.
Semplificazione delle frazioni algebriche
Per comprendere le proprietà delle frazioni algebriche, bisogna ricordare che una frazione algebrica indica semplicemente il quoziente fra il numeratore ed il denominatore. Perciò, se si indica A/B una frazione algebrica, per definizione di quoziente, si ha:
Essendo
inoltre noto che il quoziente non cambia valore se si moltiplica o
divide sia il dividendo che il divisore per uno stesso numero diverso
da zero, si può enunciare il seguente
Teorema - Una frazione algebrica è equivalente a quella che si ottiene moltiplicando o dividendo entrambi i termini della frazione per una stessa espressione diversa da zero.
Questo teorema permette di semplificare le frazioni algebriche, allo stesso modo delle frazioni aritmetiche.
Per comprendere bene come semplificare, quando è possibile, una frazione algebrica, si ragiona su qualche esempio, cominciando dal caso più semplice, considerando la frazione:
Teorema - Una frazione algebrica è equivalente a quella che si ottiene moltiplicando o dividendo entrambi i termini della frazione per una stessa espressione diversa da zero.
Questo teorema permette di semplificare le frazioni algebriche, allo stesso modo delle frazioni aritmetiche.
Per comprendere bene come semplificare, quando è possibile, una frazione algebrica, si ragiona su qualche esempio, cominciando dal caso più semplice, considerando la frazione:

Poichè i due termini della frazione hanno dei divisori letterali in comune, ed il loro M. C. D. è
3a2b5c4, dividendo numeratore e denominatore per il loro M. C. D., si ha l'uguaglianza:

La
nuova frazione così ottenuta non si può più
semplificare, perchè i suoi termini non hanno più
divisori letterali in comune, cioè, come si suol dire, sono
primi fra loro.
Quando invece si ha una frazione algebrica, nella quale almeno un termine sia un polinomio, per vedere se la si può semplicare, conviene innanzitutto vedere se il polinomio si può scomporre in un prodotto, servendosi di uno degli artifici visti in precedenza.
Se poi numeratore e denominatore hanno fattori comuni, allora si dividono entrambi i termini della frazione per il prodotto di questi fattori comuni.
Esempi di semplificazione delle seguenti frazioni:

Quando invece si ha una frazione algebrica, nella quale almeno un termine sia un polinomio, per vedere se la si può semplicare, conviene innanzitutto vedere se il polinomio si può scomporre in un prodotto, servendosi di uno degli artifici visti in precedenza.
Se poi numeratore e denominatore hanno fattori comuni, allora si dividono entrambi i termini della frazione per il prodotto di questi fattori comuni.
Esempi di semplificazione delle seguenti frazioni:


e quindi, poichè i due termini della frazione hanno in comune il fattore 2a+b, si possono dividere per il suddetto fattore entrambi i termini della frazione, ottenendo:
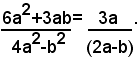
Analogamente, si ha:
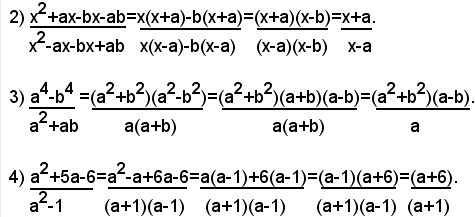
Riduzione di frazioni algebriche allo stesso denominatore
Siccome una frazione algebrica non cambia valore se si moltiplicano entrambi i termini per una stessa espressione non nulla, allora due o più frazioni si possono sempre ridurre allo stesso denominatore. Ad esempio, le due frazioni:
si possono sempre ridurre allo stesso denominatore, moltiplicando entrambi i termini della prima per il denominatore della seconda, ed entrambi i termini della seconda per il denominatore della prima. Si ottengono così le due frazioni equivalenti alle date:
Resta inteso che in pratica, talvolta è necessario prendere come denominatore comune delle frazioni un'espressione più semplice di quella data dal prodotto dei denominatori delle singole frazioni. Ad esempio, se i denominatori delle frazioni sono dei monomi, conviene prendere come denominatore comune il loro m. c. m.
Esempio: ridurre allo stesso denomonatore le seguenti frazioni:
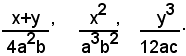
Per m. c. m. dei denominatori si può prendere 12a3b2c, e poichè si ha:
(12a3b2c):(4a2)=3abc; (12a3b2c):(6a3b2)=2c; (12a3b2c):(12ac)=a2b2, si moltiplicano ambo i termini della prima frazione per 3abc, ambo i termini della seconda per 2c ed ambo i termini della terza per a2b2, ottenendo così le nuove frazioni, equivalenti alle date:
(12a3b2c):(4a2)=3abc; (12a3b2c):(6a3b2)=2c; (12a3b2c):(12ac)=a2b2, si moltiplicano ambo i termini della prima frazione per 3abc, ambo i termini della seconda per 2c ed ambo i termini della terza per a2b2, ottenendo così le nuove frazioni, equivalenti alle date:

Se poi i denominatori delle frazioni, che si vogliono ridurre allo stesso denominatore, sono polinomi, allora si cerca anzitutto di trasformare in prodotto questi polinomi. Dopo di che si prende come denominatore comune il prodotto di tutti i fattori comuni e non comuni, che compaiono in questi prodotti, preso ciascuno una sola volta e con il maggiore degli esponenti, che esso ha nei vari denominatori.
Esempi:
1)-ridurre allo stesso denominatore le seguenti frazioni:
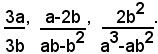
I denominatori delle frazioni, scomposti in prodotto, sono: 3b, b(b-a), a(a+b)(a-b). Si vede allora che si può assumere come denominatore comune il prodotto: 3ab(a+b)(a-b). Dividendo il denominatore comune per i denominatori delle singole frazioni, si ottengono rispettivamente i seguenti quozienti: a(a+b)(a-b), 3a(a+b), 3b; quindi le frazioni equivalenti alle date, e ridotte allo stesso denominatore, sono:


I denominatori delle frazioni, scomposti in prodotto, sono: x(x+y), (x+y)(x-y), (x+y)2, e perciò come denominatore comune si prende: x(x-y)(x+y)2; quindi le frazioni ridotte allo stesso denominatore sono:

Operazioni sulle frazioni algebriche
1)-Addizione algebrica
Per calcolare la somma di due o più frazioni algebriche. si applica la stessa regola che vale per le frazioni aritmetiche. Infatti, brevemente si indicano con:
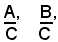
1)-Addizione algebrica
Per calcolare la somma di due o più frazioni algebriche. si applica la stessa regola che vale per le frazioni aritmetiche. Infatti, brevemente si indicano con:
due frazioni algebriche aventi lo stesso denominatore, per definizione di quoziente si ha:
da cui, sommando membro a membro:
ossia, per l'inversa della proprietà distributiva della moltiplicazione, risulta:
Ma questa uguaglianza esprime che la somma
è uguale al quoziente (A+B) e C, cioè la frazione che ha per numeratore A+B e per denominatore C. Si ha quindi:

Si può enunciare la seguente regola:
-per calcolare la somma algebrica di due o più frazioni, prima si riducono allo stesso denominatore, e poi la somma è data da quella frazione algebrica che ha per numeratore la somma algebrica dei nuovi numeratori e come denominatore il denominatore comune scelto per le frazioni date.
Naturalmente, dopo aver trovato la frazione somma, conviene, se è possibile, semplificarla.
Esempi:
1)-calcolare la seguente somma:

3)-Divisione
- Si dice reciproca o inversa di una frazione algebrica, la frazione
che moltiplicata per la prima dà per prodotto +1.
E' facile vedere che la reciproca della frazione A/B, cioè la frazione che si ottiene dalla da quella data scambiando i due termini. Infatti, per la regola del prodotto, si ha:


Per provare ciò, è sufficiente dimostrare che, per definizione di quoziente, il prodotto

moltiplicato per

Infatti, si ha:
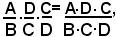
ossia, dividendo numeratore e denominatore della frazione, al secondo membro, per DC, si ottiene:

come volevasi dimostrare.
Esempi:
1)
2)
3)
Quando i termini di una frazione algebrica non sono monomi o polinomi, ma espressioni letterali contenenti a loro volta delle frazioni algebriche, è conveniente eseguire le operazioni indicate separatamente nel numeratore e nel denominatore e, infine, dividere il risultato ottenuto nel numeratore per quello ottenuto nel denominatore.
Esempio:

1)-calcolare la seguente somma:
Un denominatore comune è 12a2b2, quindi:

2)-calcolare la seguente somma:
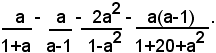
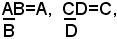
da cui, moltiplicando membro a membro, si ottiene:

ossia, per la proprietà commutativa:

Questa uguaglianza esprime che:

Si può enunciare la seguente regola:
-il prodotto di due o più frazioni algebriche è quella frazione algebrica che ha per numeratore il prodotto dei numeratori e per denominatore il prodotto dei denumeratori.
Naturalmente, dopo aver trovato la frazione algebrica prodotto, conviene, se è possibile, semplificarla.
Conseguenza della regola enunciata è poi la seguente:
-per elevare ad un qualsiasi esponente intero e positivo una frazione algebrica, basta elevare a quell'esponente entrambi i termini della frazione.
Esempi:
1)
2)
3)
4)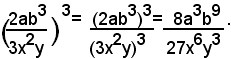
5)
Nota bene
Se vi sono dei polinomi fra i termini delle frazioni che si devono moltiplicare, è opportuno non moltiplicare i numeratori tra loro come anche i denominatori, ma conviene prima indicare le operazioni stesse in un'unica frazione. Poi si trasformano, se è possibile, i singoli polinomi in prodotto e si riduce poi la frazione ai minimi termini.
Esempio:


2)-calcolare la seguente somma:
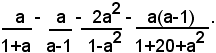
Si ha:


Un denominatore comune è (1-a)(1+a)2, quindi:

2)-Moltiplicazione ed elevamento a potenza di frazioni algebriche
Siano:
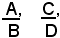

2)-Moltiplicazione ed elevamento a potenza di frazioni algebriche
Siano:
due frazioni algebriche, per definizione di quoziente, si ha:
da cui, moltiplicando membro a membro, si ottiene:
ossia, per la proprietà commutativa:
Questa uguaglianza esprime che:
Si può enunciare la seguente regola:
-il prodotto di due o più frazioni algebriche è quella frazione algebrica che ha per numeratore il prodotto dei numeratori e per denominatore il prodotto dei denumeratori.
Naturalmente, dopo aver trovato la frazione algebrica prodotto, conviene, se è possibile, semplificarla.
Conseguenza della regola enunciata è poi la seguente:
-per elevare ad un qualsiasi esponente intero e positivo una frazione algebrica, basta elevare a quell'esponente entrambi i termini della frazione.
Esempi:
1)

2)

3)
4)
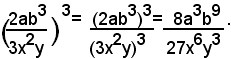
5)

Nota bene
Se vi sono dei polinomi fra i termini delle frazioni che si devono moltiplicare, è opportuno non moltiplicare i numeratori tra loro come anche i denominatori, ma conviene prima indicare le operazioni stesse in un'unica frazione. Poi si trasformano, se è possibile, i singoli polinomi in prodotto e si riduce poi la frazione ai minimi termini.
Esempio:

E' facile vedere che la reciproca della frazione A/B, cioè la frazione che si ottiene dalla da quella data scambiando i due termini. Infatti, per la regola del prodotto, si ha:
Ciò premesso, per la divisione delle frazioni algebriche, sussiste la seguente regola:
-per dividere una frazione algebrica per un'altra, basta moltiplicare la prima frazione per l'inversa della seconda, cioè:
-per dividere una frazione algebrica per un'altra, basta moltiplicare la prima frazione per l'inversa della seconda, cioè:
Per provare ciò, è sufficiente dimostrare che, per definizione di quoziente, il prodotto
moltiplicato per
dà per risultato
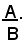
Infatti, si ha:
ossia, dividendo numeratore e denominatore della frazione, al secondo membro, per DC, si ottiene:
come volevasi dimostrare.
Esempi:
1)

2)
3)

Quando i termini di una frazione algebrica non sono monomi o polinomi, ma espressioni letterali contenenti a loro volta delle frazioni algebriche, è conveniente eseguire le operazioni indicate separatamente nel numeratore e nel denominatore e, infine, dividere il risultato ottenuto nel numeratore per quello ottenuto nel denominatore.
Esempio:
