MIKY & GENNY

MONOMI ---> INDICE

DEFINIZIONI

1 - Definizione di monomio
Si chiama monomio ogni prodotto di fattori qualsiasi, cioè uguali o disuguali, numerici o letterali, dove i fattori letterali sono elevati ad esponenti interi, positivi o nulli.
In altri termini, chiamasi monomio un'espressione algebrica in cui non figurano addizioni, sottrazioni e divisioni.
Esempi di monomi:
1) 4ab2(-5)a3(-c)7b5;
2) (-5/4)(1/3)a2x3bab3a4(+6)c.
Anche i singoli numeri, siano essi rappresentati da lettere oppure da dati aritmetici, si considerano come monomi, ad esempio sono monomi anche -2/7, c, ecc.
Le regole di calcolo letterale, già note, permettono di semplificare la scrittura di un monomio. Per la proprietà commutativa della moltiplicazione, si possono scrivere prima tutti i fattori numerici, poi tutti i fattori uguali ad a, poi tutti i fattori uguali a b ed infine il fattore (-c), cioè la 1), si può scrivere sotto la forma seguente: 3) 4(-5)7aa3b2b5(-c). Inoltre, per la proprietà dissociativa, si può sostituire ai fattori numerici il loro prodotto e ad ogni prodotto di fattori letterali, di uguale base, la corrispondente potenza. Si attibuisce, poi al monomio, quel segno (sottinteso se è +, messo in evidenza se è -), che risulta, secondo la regola, dei segni dei diversi prodotti parziali. Quindi, in definitiva, il monomio 1), ossia 3), si può srivere: 140a4b7c.
Ricapitolando: 4ab2(-5)a3(-c)7b5=4(-5)7aa3b2b5(-c)=140a4b7c.
Analogamente, il monomio 2) si può scrivere sotto la forma:
2) (-5/4)(1/3)a2x3bab3a4(+6)c=(-5/4)(1/3)(+6)a2aa4bb3cx3=-(5/2)a7b4cx3.
Quando in un monomio sono state eseguite tutte le semplificazioni, come è stato fatto nei due esempi precedenti, si dice che si è scritto il monomio sotto forma normale o ridotta.
E' bene tenere presente che: la possibilità di scrivere un monomio sotto forma normale, costituisce una semplificazione fondamentale di scrittura e che le diverse lettere che compariranno in un monomio verranno scritte in ordine alfabetico.

2 - Definizione di monomio scritto sotto forma normale o ridotta
Un monomio si dice scritto sotto forma normale, quando è un prodotto di un fattore numerico e di potenze, con esponente intero, positivo o nullo, di lettere tutte diverse fra loro.
Il fattore numerico con il suo segno (sottinteso se è +, in evidenza se è -) si chiama coefficiente del monomio, ed il prodotto dei fattori rimanenti, si chiama parte letterale del monomio.
Se in un monomio il coefficiente è +1, esso non si scrive fra i fattori del monomio e resta soltanto la parte letterale. Se invece il coefficiente è -1, allora si scrive solo la parte letterale preceduta dal segno. E' ovvio che, se il monomio si riduce alla costante +1 o -1, il coefficiente si deve scrivere.
Esempio: i tre monomi (2/3)a3bc, a4b3x, -x2y3z4, sono scritti in forma normale, ed hanno per coefficiente, rispettivamente 2/3, +1 e -1.
Se poi un monomio ha coefficiente 0, esso si chiama monomio nullo e può essere indicato semplicemente con 0, quali che siano i valori attribuiti alle lettere che voi figurano; ad esempio, invece di scrivere 0abx, si scrive semplicemente 0.
Se in monomio l'esponente di una lettera è nullo, nello scrivere il monomio, si conviene di tralasciare la lettera e l'esponente; ad esempio, invece di scrivere -7a2b0c3, si scrive -7a2c3. In particolare, un monomio con gli esponenti tutti nulli si rappresenta col simbolo stesso del suo coefficiente; ad esempio, invece di scrivere -2a0b0x0, si scrive -2.

3 - Definizione di grado di un monomio non nullo e scritto sotto forma normale rispetto ad una lettera in esso contenuta
Si chiama grado di un monomio non nullo e scritto sotto forma normale rispetto ad una lettera in esso contenuta, l'esponente che questa lettera ha nel monomio.
Ad esempio, il monomio -5a2b7c,  è di secondo grado rispetto alla lettera a, di settimo grado rispetto alla lettera b e di primo grado rispetto alla lettera c, essendo sottinteso 1 quando in una lettera non figura l'esponente.
Quando il monomio non è scritto sotto forma normale, per determinare il suo grado rispetto ad una lettera, è consigliabile prima scriverlo sotto forma normale e poi applicare la definizione precedente. Ad esempio, per determinare il grado del monomio -3a2bca3b2x, rispetto alla lettera a, prima si scrive sotto forma normale: -3a5b3cx, e quindi si vede che, rispetto alla lettera a, è di quinto grado.

4 - Definizione di un monomio non nullo di grado zero
Si dice che un monomio non nullo è di grado zero rispetto a qualsiasi lettera non contenuta in esso.
Ad esempio, il monomio -7b3c è di grado zero rispetto alla lettera a.
Questa definizione si giustifica pensando che la lettera mancante si può introdurre nel monomio come fattore con l'esponente zero, perchè la potenza di esponente zero vale 1, così il monomio precedente si può pensare scritto: -7a0b3c. In particolare si ha:
-un numero relativo, diverso da zero, è di grado zero rispetto a qualsiasi lettera.
Ad esempio, il numero -3/5 è di grado zero sia rispetto alla lettera a, sia rispetto alla lettera b, ecc.

5 - Definizione di grado di un monomio non nullo
Si chiama grado di un monomio non nullo, la somma degli esponenti di tutte le lettere contenute nel monomio.
Ad esempio, il monomio 7a2b3c è di sesto grado, mentre il monomio -7ab è di secondo grado.

Dalle definizioni date, si vede che i gradi del monomio nullo rispetto alle singole lettere, ed il grado stesso del monomio nullo, sono indeterminati, perchè può considerarsi sia come uguale a zero, che ad 1, che a due, ecc. Infatti, ad esempio il monomio nullo 0a3, si può scrivere anche sotto la forma 0a5 oppure 0a30, ecc., e perciò il suo grado può essere indifferentemente 3, oppure 5, oppure 30, o qualsiasi altro numero. In generale, per il monomio, si preferisce non parlare di grado.

6 - Definizione di monomi non nulli simili
Due monomi non nulli si dicono simili se, ridotti a forma normale, hanno la stessa parte letterale, cioè le stesse lettere con gli stessi esponenti.
I monomi simili differiscono al più nei coefficienti; ad esempio, sono simili i seguenti monomi: 7a2b5c,  -a2b5c,  -3a2b5c.

7 - Definizione di monomi non nulli uguali
Due monomi non nulli si dicono uguali se, ridotti a forma normale, hanno gli stessi coefficienti e contengono le stesse lettere, ciascuna con il medesimo esponente.
In altri termini, due monomi non nulli sono uguali, se essi sono simili ed hanno gli stessi coefficienti.

8 - Definizione di monomi non nulli opposti
Due monomi non nulli si dicono opposti, quando sono simili ed hanno coefficienti opposti.
Ad esempio, sono opposti i monomi: 3ab2 e -3ab2. Evidentemente, due monomi opposti, quali che siano i valori attribuiti alle lettere in essi contenute, assumono sempre valori fra loro opposti.

Addizione algebrica
La somma algebrica, in generale, si indica scrivendo uno dopo l'altro i monomi addendi, ciascuno con il suo segno in evidenza.
Esempio: la somma dei monomi 4a2b, -2ab3c, 9a, si indica con: 4a2b -2ab3c+9a, invece di (4a2b)+( -2ab3c)+(+9a), in quanto dopo la convenzione fatta di sottintendere il segno + dell'addizione e di scrivere i numeri relativi senza parentesi, la stessa convenzione si fa anche per la somma di più monomi.

Sottrazione algebrica
Similmente, per sottrarre da un monomio un altro monomio, come è noto, basta sommare al primo l'opposto del secondo.
Esempi:
1) 5a2b7-(-3ax3)=5a2b7+3ax3;
2) 9ac2-(4b2c3)=9ac2-4b2c3.

La somma algebrica di più monomi si può semplificare quando si deve calcolare la somma algebrica di più monomi simili
Esempio: addizionare i seguenti monomi simili: 3a2b, -7a2b, +15a2b, -a2b.
Si scrive: (1) 3a2b-7a2b+15a2b-a2b. Per la proprietà inversa della proprietà distributiva della moltiplicazione, la somma (1) si può scrivere sotto la seguente forma: (2) (3-7+15-1)a2b, e osservato che (3-7+15-1)=10, il monomio (2) si può scrivere sotto la forma 10a2b.
Si può quindi dire che la somma di quattro monomi simili considerati è un monomio simile ai dati e che ha per coefficiente la somma algebrica dei coefficienti dei monomi dati. Quanto constatato in tale esempio, vale in generale, cioè una somma di monomi simili si può sempre ridurre ad un solo monomio. Si può quindi enunciare la seguente regola:
-la somma algebrica di monomi simili è un monomio simile ai dati che ha per coefficiente la somma algebrica dei coefficienti dei monomi addendi.
Questa notevole semplificazione di scrittura è dovuta alla proprietà distributiva della moltiplicazione.
Da quanto visto, si può dire che, quando si incontra una somma algebrica di monomi, bisogna controllare se fra essi vi sono monomi simili, ed in caso affermativo, i monomi simili si addizionano con la regola enunciata, e la somma algebrica considerata viene così scritta sotto forma semplificata. In ciò consiste la cosiddetta riduzione dei termini simili.
Esempi di riduzione dei monomi simili delle seguenti somme algebriche di monomi:
1) -6a+7b+9a-4a-9b+15b-a.
Praticamente, conviene sottolineare con uno stesso segno tutti i monomi simili fra loro, per esseri sicuri di averli considerati tutti; si ottiene:
1) -6a+7b+9a-4a-9b+15b-a=-2a+13b.
2) 3a3b2-3ab4-2a3b2-5ab4+2ab-2ab4=a3b2-10ab4+2ab.
3) 3a3b2c-3a2bc2-4a3b2-5a3b2c-3a2bc2=-a3b2c-6a2bc2-4a3b2.
4) 5a3+a2b-3ab2+7b3+3a3-a2b+5ab2-5b3=8a3+2ab2+2b3.

Moltiplicazione ed elevamento a potenza dei monomi
Siccome un monomio è un prodotto, per il teorema "Per moltiplicare fra loro due o più prodotti indicati, basta formare un unico prodotto con tutti i fattori dei prodotti dati.", il prodotto di più monomi è un unico monomio che contiene tutti e soltanto i fattori dei monomi considerati. Il monomio così ottenuto si riduce poi a forma normale, tenendo presente che il prodotto di potenze aventi la stessa base è una potenza che ha per base la stessa base e per esponente la somma degli esponenti.
Esempio di calcolo del prodotto dei due monomi: 7a2bcx, 15a3b2c5y2.
Si ha: (7a2bcx)(15a3b2c5y2)=7a2bcx15a3b2c5y2=(7·15)(a2a3)(bb2)(cc5)xy2=105a5b3c6xy2.

Si osserva ora che:
a)-il coefficiente del monomio prodotto è uguale al prodotto dei coefficienti dei monomi fattori;
b)-l'esponente che ogni lettera assume nel prodotto è la somma degli esponenti con i quali essa figura nei singoli fattori, contando zero il suo esponente in quei monomi fattori in cui essa eventualmente manca;
c)-il grado del monomio prodotto ottenuto è uguale alla somma dei gradi dei monomi fattori.
Esempio di calcolo del prodotto dei monomi -2abc3, 5b3cd, 3a9c5. Si ha:
(-2abc3)(5b3cd)(3a9c5)=-2aba2b55b3cd3a9c5=(-2·5·3)(aa9)(bb3)(c3cc5)(d)=-30a10b4c9d.
Si vede che anche in questo caso il monomio prodotto gode delle proprietà a) e b) sopra enunciate, ed inoltre il suo grado è sempre uguale alla somma dei gradi dei monomi fattori.
Il metodo è generale e conduce alla seguente regola:
-il prodotto di due o più prodotti non nulli è un monomio avente per coefficiente il prodotto dei coefficienti e la cui parte letterale è costituita da tutte le lettere che figurano nei singoli monomi, con esponenti uguali alla somma degli esponenti che le stesse lettere hanno nei monomi dati. Il grado del monomio prodotto è uguale alla somma dei gradi dei monomi fattori, purchè questi siano diversi dal monomio nullo.
E' evidente poi che il prodotto di due o più monomi è uguale al monomio nullo solo quando almeno uno dei monomi fattori è nullo.
Esempi:
1) (3ab2)(-5ab)(4b2)=-60a2b5;
2) (2a2bc4)(-5ab2c3)(-2a5bc2)=20a8b4c9;
3) 5ab2x(-a3)(+5ab2c)(-3bx3)(-3ax)=-225a6b5cx5.
Esempi di calcolo dei prodotti dei monomi nella seguente somma e riduzione dei monomi simili:
4) 5a2(-ab)+(-2a5b)(+3b)+(-7a3)(-2b)+(+a3b2)(-2a2)=-5a3b-6a5b2+14a3b+a5b2=9a3b-5a5b2.

Tenendo presente che un monomio è un prodotto di più fattori e ricordando i teoremi 3) e 4) sulle potenze, si ha la seguente regola:
-per elevare a potenza n-esima un monomio, con n intero positivo, si eleva a quella potenza il coefficiente e si moltiplicano per n gli esponenti dei fattori letterali.

Esempi:



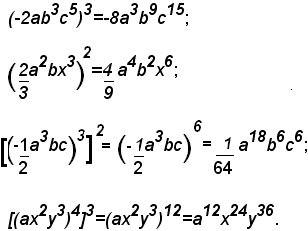
Calcolare le potenze dei monomi, i prodotti dei monomi e ridurre infine i termini simili, nella seguente espressione:


Calcolando prima le potenze, poi i prodotti indicati ed infine riducendo i termini simili, si ottiene:



Spesso, la regola enunciata si applica in senso inverso, pertanto se si vuole scrivere sotto forma di quadrato un monomio, ad esempio, si ha:



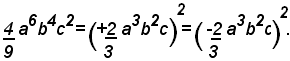
Se invece si vuole scrivere sotto forma di cubo un monomio, ad esempio, si ha:



Definizione di divisione di monomi
Si dice che un monomio è divisibile per un altro monomio, non nullo, quando esiste un terzo monomio che moltiplicato per il secondo, dà il primo.
Da tale definizione segue che il monomio nullo è divisibile per ogni monomio non nullo.
E' evidente che, quando un monomio, dividendo, è divisibile per un altro monomio, divisore, la regola che permette di trovare il monomio quoziente è una conseguenza immediata della regola della moltiplicazione, e del fatto che il quoziente di due potenze aventi la stessa base è uguale ad una potenza avente la stessa base e per esponente, la differenza degli esponenti.
Esempio: (12a7b3c):(4a3b2)=(12:4)a7-3b3-2c=3a4bc.
Infatti: (4a3b2)(3a4bc)=12a7b3c.
Si può quindi enunciare la seguente regola:
-il quoziente di due monomi, non nulli e divisibili, è un monomio che ha per coefficiente il quoziente dei coefficienti dei due monomi dati e come parte letterale quella che si ottiene dalla parte letterale del dividendo, sottraendo dall'esponente di ciascuna sua lettera l'esponente che la stessa lettera ha nel divisore.
Tale regola presuppone che i due monomi sono divisibili, cioè ammette che esiste un monomio che moltiplicato per il secondo dà il primo. Ma, evidentemente, perchè esista il quoziente di due monomi, è necessario e sufficiente che la regola enunciata si possa applicare. Ebbene, perchè questa regola sia applicabile, si vede che il monomio dividendo deve contenere tutte le lettere del monomio divisore, elevata ciascuna ad un esponente maggiore, o almeno uguale, a quello con cui la stessa lettera figura nel monomio divisore.
Si può quindi dire che:
-perchè un monomio non nullo sia divisibile per un altro monomio non nullo, è necessario e sufficiente che ogni lettera del monomio divisore fuguri nel monomio dividendo con esponente uguale o maggiore.
In particolare si ha quindi che:
-ogni monomio è divisibile per qualsiasi numero diverso da zero.
Esempi:
1) (-2/3)a3b:9=(-2/27)a3b;
2) 4x2y2:(-3/5)=(-20/3)x2y2;
3) (9/4)xy:(3/7)=(21/4)xy.
Quando un monomio non è divisibile per un altro, allora la divisione dell'uno per l'altro non si può indicare. Ad esempio, la divisione del monomio 7a2b per il monomio 5xy si indica nel modo seguente: (7a2b):(5xy) oppure con 7a2b/5xy, ottenendo così un monomio frazionario.
Esempio 1): eseguire le operazioni indicate e poi ridurre i termini simili nella seguente somma algebrica:


Massimo comune divisore e minimo comune multiplo di due o più monomi.
Considerati i monomi (1) 4a5b3c4d2; (-5/2)a4b2c3; 9a3b(1)d, si forma il monomio che ha per parte letterale soltanto tutte le lettere comuni ai tre monomi dati, elevate al più piccolo esponente che essa ha nei tre monomi, e per coefficiente, ad esempio +1. Il monomio cercato è (2) a3bc2, che evidentemente divide ciascuno dei tre monomi dati. E' bene osservare che i tre monomi (1) ammettono altri monomi, diversi dal monomio (2), che li divide tutti e tre; ad esempio, i monomi a, ac2, a2bc, ecc. Però tutti questi altri divisori sono monomi di grado inferiore a quello del del monomio (2), anzi essi sono divisori del monomio (2). Si può quindi dire che che fra tutti i monomi che dividono simultaneamente i tre monomi dati, il monomio a3bc2 è quello che ha il massimo grado rispetto a ciascuna lettera. E' naturale allora, conformemente a quanto si è fatto per i numeri interi, chiamare il monomio a3bc2, massimo comune divisore dei monomi considerati. Finora, non si è detto nulla sul coefficiente da attibuire al monomio (2), e questo perchè, quale che sia il coefficiente che si attibuisce al monomio a3bc2, si ottiene sempre un monomio che divide esattamente quelli dati. Infatti, basta ricordare che ogni monomio è divisibile per qualsiasi numero diverso da zero.
Si vede che dal massimo comune divisore dei monomi (1) è individuata soltanto la parte letterale, potendo il coefficiente essere preso ad arbitrio, purchè diverso da zero. Da queste considerazioni, segue la seguente definizione:
-si chiama massimo comune divisore di due o più monomi , non tutti nulli, ogni monomio di grado massimo che divide simultaneamente tutti i monomi dati.
Il massimo comune divisore di due o più monomi si indica ancora con la scrittura M. C. D.
Nella definizione, si è detto ogni "monomio", perchè del M. C. D. di più monomi è determinata solo la parte letterale, potendosi il coefficiente prendere arbitrariamente, purchè diverso da zero. Quindi, mentre il M. C. D. di più numeri interi è un numero ben determinato, invece il M. C. D. di più monomi è determinato a meno del coefficiente.
Per trovare poi il M. C. D. di più monomi si applica la seguente regola, che in sostanza è analoga a quella che si usa per trovare il M. C. D. di più numeri interi con il metodo della scomposizione in fattori primi, vista in aritmetica:
-la parte letterale del M. C. D. di più monomi, non tutti nulli, è formata da tutte e soltanto le lettere comuni ai monomi non nulli, elevate ciascuna al più piccolo esponente che essa ha nei singoli monomi.
Si dà inoltre la seguente definizione:
-Più monomi, non tutti nulli, si dicono fra loro primi, quando il loro M. C. D. è un monomio di grado zero, cioè un numero non nullo.

Nota bene
Siccome per i numeri interi è definito il M. C. D., allora, nelle applicazioni pratiche è, in generale, conveniente prendere per coefficiente del M. C. D. di due o più monomi dati, a coefficienti interi, il M. C. D. dei loro coefficienti preceduto dal segno +. Nulla si può dire invece se i coefficienti dei monomi sono frazionari, perchè per i numeri frazionari, non ha senso parlare di M. C. D., in quanto ogni numero frazionario è divisibile per qualsiasi altro numero, diverso da zero.
Esempi di calcolo del M. C. D. dei seguenti monomi:
1) 14a2b3c; -35a4b5c2d; 42a3b4c5f.
Il M. C. D. cercato è, per quanto detto, il monomio 7a2b3c, oppure ogni altro monomio ad esso simile, ad esempio: 5a2b2c; (-3/2)a2b3c; ecc.
2) 5x2y3z; (-10/3) x3y; 15x5y3z; (-25/6)x4z2.
Il M. C. D. cercato è x2y, oppure ogni altro monomio ad esso simile, ad esempio: 5x2y; (5/3)x2y; ecc.
3) (2/3)ab2; (4/5)x2y3; (16/7)a3x.
Il M. C. D. cercato è il monomio 1, o qualsiasi altro numero diverso da zero.

Le considerazioni fatte per introdurre il M. C. D. di due o più monomi, si possono ripetere per introdurre il minimo comune multiplo di due o più monomi.
-Si chiama minimo comune multiplo di due o più monomi non nulli, ogni monomio non nullo e di grado minimo che sia divisibile contemporaneamente per tutti i monomi dati. Il minimo comune multiplo di due o più monomi si indica ancora con la scrittura m. c. m.
Per trovare il m. c. m. di due o più monomi, si applica la seguente regola, che in sostanza è analoga a quella che si usa per trovare il m. c. m. di più numeri interi con il metodo della scomposizione in fattori primi, vista in aritmetica:
-la parte letterale del m. c. m. di più monomi, non tutti nulli, è formata da tutte le lettere comuni e non comuni dei monomi dati, presa ciascuna con il più grande esponente che essa ha nei singoli monomi.
Anche per il m. c. m. di più monomi è determinata quindi la sola parte letterale, potendosi prendere come coefficiente un qualsiasi numero diverso da zero. Quando i coefficienti dei monomi dati sono numeri interi, è in generale conveniente assumere come coefficiente del monomio m. c. m., il m. c. m. dei coefficienti, preceduto dal segno +, in modo analogo a quanto si è fatto per il M. C. D.
Esempi di calcolo del m. c. m. dei seguenti monomi:
1) 9a3b2; -12ab4c2; 27b3z.
Il m. c. m. cercato è, per quanto detto, il monomio 108a3b4c2z, dove 108 è il m. c. m. dei coefficienti dei monomi dati, oppure ogni altro monomio ad esso simile, ad esempio: 9a3b4c2z; (-3/5)a3b4c2z; ecc.
2) (2/5)xy2; (-1/3) x3z; 7z5.
ll m. c. m. cercato è, x3y2z5, oppure ogni altro monomio ad esso simile.

Nota bene
Finora, nella definizione di grado di un monomio, si è supposto che la parte letterale fosse composta tutta da variabili. In seguito si avrà l'occasione di considerare monomi nei quali una o più lettere si dovranno considerare costanti, cioè lettere rappresentanti numeri noti; si dovranno perciò considerare come facenti parte del monomio stesso. Ad esempio, nei monomi nelle tre variabili x, y, z: 3ax2yz3; -5a2bxyz9; 7a3b2x2y3z3, le lettere a, b, c, devono considerarsi numeri noti. Così i coefficienti di questi tre monomi sono i numeri 3a, -5a2b, 7a3b2. Di questo fatto si deve tenere conto quando si vuole calcolare il grado di un monomio e considerare quindi gli esponenti delle sole variabili. Così il primo monomio è di sesto grado, perchè 3a è un numero fisso; il secondo è di undicesimo grado, perchè -5a2b è un numero fisso; infine, il terzo monomio è di ottavo grado, perchè 7a3b2 è un numero fisso. Si deve tenere conto anche di quanto è stato detto per i monomi simili; ad esempio i monomi nelle variabili x e y: 3x2y; a2bx2y, -5bx2y, sono simili, perchè hanno la stessa parte letterale con gli stessi esponenti, x2y, dato che 3, a2b, -5b, sono numeri e quindi rappresentano rispettivamente i coefficienti dei tre monomi.
La somma dei tre monomi simili considerati è il monomio (3+a2b -5b)x2y, il cui coefficiente è il numero 3+a2b -5b. Così, ad esempio, la somma dei seguenti monomi nelle variabili x, y, z: ax2yz+3bxy3+a2bx2yz+cxy3+2xyz+2, riducendo i monomi simili, si può scrivere sotto la forma: (a+a2b)x2yz+(3b+c)xy3+2xyz+2.