MIKY & GENNY
POTENZE CON ESPONENTE REALE ---> INDICE
Premessa
Sia α un numero reale positivo e β un qualsiasi numero reale, si vuole dare un significato al simbolo:
A tale scopo si dimostrano prima alcune proprietà delle potenze con esponente reale, ricordando che il quoziente di an-bn per a-b, è: an-1+ban-2+b2an-3+....+bn-2a+bn-1, cioè un polinomio omogeneo completo di grado n-1, ordinato secondo le potenze decrescenti della prima base e crescenti della seconda, con tutti i coefficienti uguali a 1. Si ha così l'uguaglianza:
e, ponendo in essa b=1, si ottiene
(1) an-1=(a-1)(an-1+an-2+an-3+....+a +1).
Teorema 1 - Se α è un numero reale maggiore di 1 e G un numero reale positivo, grande a piacere, è sempre possibile trovare un numero intero positivo p in modo che risulti:
(2) αp>G.
Infatti, poichè nella (1) la somma
an-1+an-2+an-3+....+a +1
è costituita da n termini, di cui l'ultimo è 1 e gli altri per ipotesi sono maggiori di 1, si ha:
an-1+an-2+an-3+....+a +1>1+1+1+....1+1=n.
Pertanto, dalla (1) segue:
an-1>(a-1)n,
ossia
(3) an>1+(a-1)n.
Si indica ora con p un numero intero positivo, scelto in modo che risulti:
(4) 1+(a-1)p>G.
e ciò e sempre possibile, in quanto basta prendere per p un numero intero in modo tale che risulti

Infatti, per

tenendo conto che a-1>0, si ha:

ossia
1+(a-1)p>1+G-1,
cioè
1+(a-1)p>G.
Quindi, scelto in tal modo il numero p, la (3) per n=p diventa:
ap>1+(a-1) p
e per la (4) si ha:
αp>G.
Ciò è quanto si voleva dimostrare.
Nota bene
Si ricorda che: una potenza avente la base maggiore di 1 ed esponente razionale, aumenta all'aumentare dell'esponente; perciò, trovato il numero p tale che si verifichi la disuguaglianza αp>G, ogni altro numero razionale maggiore di p la verifica pure. Inoltre, il teorema 1 afferma che una tale potenza, all'aumentare del suo esponente, può assumere valori grandi desiderati, dato che il numero G si può fissare grande a piacere.
Teorema 2 - Se α è un numero reale positivo minore di 1 ed ε un numero positivo, piccolo a piacere, è sempre possibile determinare un numero intero positivo p in modo che risulti:
(5) αp>ε.
Essendo α un numero reale positivo minore di 1, cioè 0<a<1, risulta:

Fissato allora un numero positivo ε, piccolo a piacere e considerato il numero
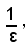
questo risulta un numero grande a piacere; in sua corrispondenza, per il teorema precedente, si può trovare un numero intero positivo p, in modo che risulti:

cioè

e considerati i reciproci, tenendo conto che essendo i due numeri positivi si deve cambiare il verso della disuguaglianza, si ha:
ap<ε .
Ciò è quanto si voleva dimostrare.
Nota bene
Si ricorda che: una potenza avente la base positiva minore di 1 ed esponente razionale, diminuisce all'aumentare dell'esponente; perciò, trovato il numero p in modo tale che verifichi la disuguaglianza αp<ε, ogni altro numero razionale maggiore di p la verifica pure. Inoltre, il teorema 2 afferma che una tale potenza, all'aumentare del suo esponente, può assumere valori piccoli desiderati, dato che il numero ε si può fissare piccolo a piacere.
Teorema 3 - Se α è un numero reale maggiore di 1 ed ε un numero positivo, piccolo a piacere, è sempre possibile determinare un numero intero positivo p in modo che risulti: (6)
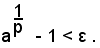
Infatti, essendo 1+ ε>1, per il teorema 1, si può sempre determinare un numero intero positivo p, in modo che risulti:
(7) (1+ε)p>a .
Elevando ambo i membri della (7) alla potenza di esponente 1/p, si ha:

ed essendo, per una proprietà sulle potenze
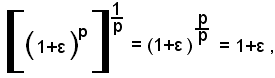
in definitiva si ha

ossia

cioè
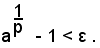
Ciò è quanto si voleva dimostrare.
Nota bene
Siccome una potenza avente la base maggiore di 1 ed esponente razionale, diminusce al diminuirere dell'esponente, allora, trovato un numero 1/p tale che si verifichi la disuguaglianza (6), ogni altro numero razionale positivo minore di 1/p la verifica pure. Inoltre, il teorema 3 afferma che una tale potenza, al diminuire del suo esponente, per valori razionali positivi, può assumere i valori prossimi ad 1, dato che il numero ε si può fissare piccolo a piacere.
In modo analogo si dimostra il teorema 4.
Teorema 4 - Se α è un numero reale positivo minore di 1 ed ε un numero positivo, piccolo a piacere, è sempre possibile determinare un numero positivo p in modo che risulti:

Potenze con esponente reale
E' noto che una sezione (A, B) fatta con numeri reali è di prima specie, cioè una sezione (A, B) del campo reale esclude sempre uno ed un solo numero reale λ, il quale risulta maggiore di tutti i numeri reali contenuti in A e minore di tutti i numeri reali contenuti in B. Tale elemento si chiama elemento di separazione delle due classi A e B. Per indicare ciò, si scrive:
λ=(A, B).
Si definisce ora la potenza avente per base un numero reale positivo α e per esponente un qualsiasi numero reale β:
Si distinguono i seguenti casi:
1° Caso: α>1 e β>0
Si indicano con H e K due classi di numeri razionali, costituenti la sezione che definisce il numero reale β, cioè sia:
β=(H, K).
Si osserva prima che, se h è un numero razionale appartenente alla classe H, ha senso parlare della potenza αh, perchè α>0 e h indica un numero razionale.
Il numero rappresentato poi dalla potenza αh può essere sia razionale che irrazionale, a seconda del valore di α e del valore scelto per h fra i numeri della classe H.
Ad esempio, se α=5 e in H è contenuto il numero 1/2, si ha:

Questo numero è irrazionale.
Se poi in H è contenuto anche il numero 3, allora il numero 5=1253 è razionale.
Perciò si può soltanto dire che αh è un numero reale positivo.
Premesso ciò, se h1 è un numero di H, si mettono in una classe F il numero ah1 e tutti i numeri reali minori di esso e così si procede anche per tutti gli altri numeri che si ottengono elevando α ad una potenza avente per esponente un numero di H. In altri termini, se h2 è un numero di H, diverso da h1, nella classe F si mettono anche ah2 e tutti i numeri reali minori di questo, ecc.
Allo stesso modo, si indica con G la classe dei numeri reali che si ottiene mettendo in corrispondenza di ogni numero razionale k appartenente alla classe K, il numero ak e tutti i numeri reali maggiori di esso. Le due classi F e G costituiscono una sezione, come si potrebbe dimostrare e ci si limita solo all'enunciato, nel campo dei numeri reali e perciò definiscono un ben determinato numero reale positivo, nel senso che esiste uno ed un solo numero reale che è maggiore di tutti i numeri reali contenuti in F e minore di tutti i numeri reali contenuti in G. Questo numero si assume, come potenza αβ di base α ed esponente β, cioè si pone per definizione:
Definizione - Dato un numero reale α maggiore di 1 ed un numero reale positivo β=(H, K), si chiama potenza di base α ed esponente β, e si indica αβ, il numero reale positivo che rappresenta l'elemento di separazione della sezione dei numeri reali, ottenuta ponendo nella classe inferiore F tutti i numeri reali del tipo αh, con h numero razionale di H e tutti quelli minori di essi, e nella classe superiore G tutti i numeri reali del tipo αk, con k numero razionale di K e tutti quelli maggiori di essi. Cioè si pone:
αβ=(F, G).
Si osservi ora che nella classe F ci sono anche ci sono anche tutti i numeri del tipo αh, con h numero razionale di H, cioè in F ci sono le potenze che si ottengono elevando successivamente il numero α a tutti i numeri razionali che formano la classe inferiore H del numero β. In G ci sono invece anche tutte le potenze del tipo αk, con k numero razionale della classe superiore K di β. Perciò il numero αβ, essendo l'elemento di separazione della sezione (F, G), soddisferà le seguenti limitazioni:
αh<αβ<αk,
quali che siano i numeri h della classe H e k della classe K.
Quindi si può dire che:
-il numero αβ è compreso fra le potenze di α aventi per esponenti tutti i numeri razionali minori di β e le potenze di α aventi per esponenti tutti i numeri razionali maggiori di β.
Nota beneSe si considera (1)
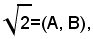
dove le classi A e B di numeri razionali hanno il significato noto, si vuole vedere cosa rappresenta il simbolo

Tale simbolo rappresenta un numero reale, precisamente:
-si calcolano tutte le potenze aventi base 7 ed esponenti uguali ai numeri razionali contenuti nella classe A e tutti questi numeri, insieme a quelli minori di essi, si mettono nella classe F;
-si calcolano tutte le potenze aventi base 7 ed esponenti uguali ai numeri razionali contenuti nella classe B e tutti questi numeri reali, insieme a quelli maggiori di essi, si mettono nella classe G.
Pertanto il simbolo in questione indica il numero reale che è l'elemento di separazione della sezione (F, G), cioè quel mumero reale che è maggiore di tutti i numeri contenuti in F e minore di tutti quelli contenuti in G.
Se si considera (2)

si vuole vedere cosa rappresenta il simbolo

-Si calcolano tutte le potenze aventi per base radice di 5 ed esponenti uguali ai numeri razionali contenuti nella classe C e tutti questi numeri, insieme a quelli minori di essi, si mettono in una classe in una classe R.
-Si calcolano tutte le potenze aventi base radice di 5 ed esponenti uguali ai numeri razionali contenuti nella classe D e tutti questi numeri, insieme a quelli maggiori di essi, si mettono in una classe S.
Pertanto il simbolo in questione indica il numero reale che è l'elemento di separazione della sezione (R, S).
2° Caso: 0<a<1 e β>0.
Si possono fare considerazioni del tutto analoghe a quelle del 1° caso, però in questo bisogna ricordare che essendo 0<α<1, le potenze con esponente razionale di α diminuscono all'aumentare dell'esponente, mentre aumentono al diminuire dell'esponente. Quindi, in questo caso, bisogna mettere in F tutti i numeri del tipo αk e quelli minori di essi e nella classe G tutti i numeri del tipo αhe quelli maggiori di essi.
Definizione - Dato un numero reale positivo α minore di 1 ed un numero reale positivo β=(H, K), si chiama potenza di base α ed esponente β, e si indica αβ, il numero reale positivo che rappresenta l'elemento di separazione della sezione di numeri reali, ottenuta ponendo nella classe inferiore F tutti i numeri reali del tipo αk, con k numero razionale di K e tutti quelli minori di essi, e nella classe superiore G tutti i numeri reali del tipo αh, con h numero razionale di H e tutti quelli maggiori di essi. Cioè si pone:
αβ=(F, G).
3° Caso: α>0 e β<0.
In questo caso, tanto per α>1, quanto per 0<α<1, come nel caso degli esponenti razionali, si pone, per definizione:

tenendo presente che, essendo per ipotesi β<0, risulta -β>0, pertanto la potenza α-β è stata definita precedentemente sia per α>1, sia per 0<α<1.
Si completa poi la definizione di potenza reale, ponendo:
Sia α un numero reale positivo e β un qualsiasi numero reale, si vuole dare un significato al simbolo:
αβ.
A tale scopo si dimostrano prima alcune proprietà delle potenze con esponente reale, ricordando che il quoziente di an-bn per a-b, è: an-1+ban-2+b2an-3+....+bn-2a+bn-1, cioè un polinomio omogeneo completo di grado n-1, ordinato secondo le potenze decrescenti della prima base e crescenti della seconda, con tutti i coefficienti uguali a 1. Si ha così l'uguaglianza:
an-bn=(a-b)(an-1+ban-2+b2an-3+....+bn-2a+bn-1)
e, ponendo in essa b=1, si ottiene
(1) an-1=(a-1)(an-1+an-2+an-3+....+a +1).
Teorema 1 - Se α è un numero reale maggiore di 1 e G un numero reale positivo, grande a piacere, è sempre possibile trovare un numero intero positivo p in modo che risulti:
(2) αp>G.
Infatti, poichè nella (1) la somma
an-1+an-2+an-3+....+a +1
è costituita da n termini, di cui l'ultimo è 1 e gli altri per ipotesi sono maggiori di 1, si ha:
an-1+an-2+an-3+....+a +1>1+1+1+....1+1=n.
Pertanto, dalla (1) segue:
an-1>(a-1)n,
ossia
(3) an>1+(a-1)n.
Si indica ora con p un numero intero positivo, scelto in modo che risulti:
(4) 1+(a-1)p>G.
e ciò e sempre possibile, in quanto basta prendere per p un numero intero in modo tale che risulti
Infatti, per
tenendo conto che a-1>0, si ha:
ossia
cioè
1+(a-1)p>G.
Quindi, scelto in tal modo il numero p, la (3) per n=p diventa:
ap>1+(a-1) p
e per la (4) si ha:
αp>G.
Ciò è quanto si voleva dimostrare.
Nota bene
Si ricorda che: una potenza avente la base maggiore di 1 ed esponente razionale, aumenta all'aumentare dell'esponente; perciò, trovato il numero p tale che si verifichi la disuguaglianza αp>G, ogni altro numero razionale maggiore di p la verifica pure. Inoltre, il teorema 1 afferma che una tale potenza, all'aumentare del suo esponente, può assumere valori grandi desiderati, dato che il numero G si può fissare grande a piacere.
Teorema 2 - Se α è un numero reale positivo minore di 1 ed ε un numero positivo, piccolo a piacere, è sempre possibile determinare un numero intero positivo p in modo che risulti:
Essendo α un numero reale positivo minore di 1, cioè 0<a<1, risulta:
Fissato allora un numero positivo ε, piccolo a piacere e considerato il numero
questo risulta un numero grande a piacere; in sua corrispondenza, per il teorema precedente, si può trovare un numero intero positivo p, in modo che risulti:

cioè

e considerati i reciproci, tenendo conto che essendo i due numeri positivi si deve cambiare il verso della disuguaglianza, si ha:
ap<ε .
Ciò è quanto si voleva dimostrare.
Nota bene
Si ricorda che: una potenza avente la base positiva minore di 1 ed esponente razionale, diminuisce all'aumentare dell'esponente; perciò, trovato il numero p in modo tale che verifichi la disuguaglianza αp<ε, ogni altro numero razionale maggiore di p la verifica pure. Inoltre, il teorema 2 afferma che una tale potenza, all'aumentare del suo esponente, può assumere valori piccoli desiderati, dato che il numero ε si può fissare piccolo a piacere.
Teorema 3 - Se α è un numero reale maggiore di 1 ed ε un numero positivo, piccolo a piacere, è sempre possibile determinare un numero intero positivo p in modo che risulti: (6)
Infatti, essendo 1+ ε>1, per il teorema 1, si può sempre determinare un numero intero positivo p, in modo che risulti:
(7) (1+ε)p>a .
Elevando ambo i membri della (7) alla potenza di esponente 1/p, si ha:

ed essendo, per una proprietà sulle potenze
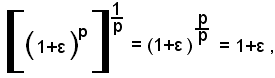
in definitiva si ha
ossia
cioè
Ciò è quanto si voleva dimostrare.
Nota bene
Siccome una potenza avente la base maggiore di 1 ed esponente razionale, diminusce al diminuirere dell'esponente, allora, trovato un numero 1/p tale che si verifichi la disuguaglianza (6), ogni altro numero razionale positivo minore di 1/p la verifica pure. Inoltre, il teorema 3 afferma che una tale potenza, al diminuire del suo esponente, per valori razionali positivi, può assumere i valori prossimi ad 1, dato che il numero ε si può fissare piccolo a piacere.
In modo analogo si dimostra il teorema 4.
Teorema 4 - Se α è un numero reale positivo minore di 1 ed ε un numero positivo, piccolo a piacere, è sempre possibile determinare un numero positivo p in modo che risulti:
Potenze con esponente reale
E' noto che una sezione (A, B) fatta con numeri reali è di prima specie, cioè una sezione (A, B) del campo reale esclude sempre uno ed un solo numero reale λ, il quale risulta maggiore di tutti i numeri reali contenuti in A e minore di tutti i numeri reali contenuti in B. Tale elemento si chiama elemento di separazione delle due classi A e B. Per indicare ciò, si scrive:
λ=(A, B).
Si definisce ora la potenza avente per base un numero reale positivo α e per esponente un qualsiasi numero reale β:
αβ.
Si distinguono i seguenti casi:
1° Caso: α>1 e β>0
Si indicano con H e K due classi di numeri razionali, costituenti la sezione che definisce il numero reale β, cioè sia:
β=(H, K).
Si osserva prima che, se h è un numero razionale appartenente alla classe H, ha senso parlare della potenza αh, perchè α>0 e h indica un numero razionale.
Il numero rappresentato poi dalla potenza αh può essere sia razionale che irrazionale, a seconda del valore di α e del valore scelto per h fra i numeri della classe H.
Ad esempio, se α=5 e in H è contenuto il numero 1/2, si ha:
Questo numero è irrazionale.
Se poi in H è contenuto anche il numero 3, allora il numero 5=1253 è razionale.
Perciò si può soltanto dire che αh è un numero reale positivo.
Premesso ciò, se h1 è un numero di H, si mettono in una classe F il numero ah1 e tutti i numeri reali minori di esso e così si procede anche per tutti gli altri numeri che si ottengono elevando α ad una potenza avente per esponente un numero di H. In altri termini, se h2 è un numero di H, diverso da h1, nella classe F si mettono anche ah2 e tutti i numeri reali minori di questo, ecc.
Allo stesso modo, si indica con G la classe dei numeri reali che si ottiene mettendo in corrispondenza di ogni numero razionale k appartenente alla classe K, il numero ak e tutti i numeri reali maggiori di esso. Le due classi F e G costituiscono una sezione, come si potrebbe dimostrare e ci si limita solo all'enunciato, nel campo dei numeri reali e perciò definiscono un ben determinato numero reale positivo, nel senso che esiste uno ed un solo numero reale che è maggiore di tutti i numeri reali contenuti in F e minore di tutti i numeri reali contenuti in G. Questo numero si assume, come potenza αβ di base α ed esponente β, cioè si pone per definizione:
αβ=(F, G).
Definizione - Dato un numero reale α maggiore di 1 ed un numero reale positivo β=(H, K), si chiama potenza di base α ed esponente β, e si indica αβ, il numero reale positivo che rappresenta l'elemento di separazione della sezione dei numeri reali, ottenuta ponendo nella classe inferiore F tutti i numeri reali del tipo αh, con h numero razionale di H e tutti quelli minori di essi, e nella classe superiore G tutti i numeri reali del tipo αk, con k numero razionale di K e tutti quelli maggiori di essi. Cioè si pone:
αβ=(F, G).
Si osservi ora che nella classe F ci sono anche ci sono anche tutti i numeri del tipo αh, con h numero razionale di H, cioè in F ci sono le potenze che si ottengono elevando successivamente il numero α a tutti i numeri razionali che formano la classe inferiore H del numero β. In G ci sono invece anche tutte le potenze del tipo αk, con k numero razionale della classe superiore K di β. Perciò il numero αβ, essendo l'elemento di separazione della sezione (F, G), soddisferà le seguenti limitazioni:
αh<αβ<αk,
quali che siano i numeri h della classe H e k della classe K.
Quindi si può dire che:
-il numero αβ è compreso fra le potenze di α aventi per esponenti tutti i numeri razionali minori di β e le potenze di α aventi per esponenti tutti i numeri razionali maggiori di β.
Nota bene
dove le classi A e B di numeri razionali hanno il significato noto, si vuole vedere cosa rappresenta il simbolo
Tale simbolo rappresenta un numero reale, precisamente:
-si calcolano tutte le potenze aventi base 7 ed esponenti uguali ai numeri razionali contenuti nella classe A e tutti questi numeri, insieme a quelli minori di essi, si mettono nella classe F;
-si calcolano tutte le potenze aventi base 7 ed esponenti uguali ai numeri razionali contenuti nella classe B e tutti questi numeri reali, insieme a quelli maggiori di essi, si mettono nella classe G.
Pertanto il simbolo in questione indica il numero reale che è l'elemento di separazione della sezione (F, G), cioè quel mumero reale che è maggiore di tutti i numeri contenuti in F e minore di tutti quelli contenuti in G.
Se si considera (2)
si vuole vedere cosa rappresenta il simbolo
-Si calcolano tutte le potenze aventi per base radice di 5 ed esponenti uguali ai numeri razionali contenuti nella classe C e tutti questi numeri, insieme a quelli minori di essi, si mettono in una classe in una classe R.
-Si calcolano tutte le potenze aventi base radice di 5 ed esponenti uguali ai numeri razionali contenuti nella classe D e tutti questi numeri, insieme a quelli maggiori di essi, si mettono in una classe S.
Pertanto il simbolo in questione indica il numero reale che è l'elemento di separazione della sezione (R, S).
2° Caso: 0<a<1 e β>0.
Si possono fare considerazioni del tutto analoghe a quelle del 1° caso, però in questo bisogna ricordare che essendo 0<α<1, le potenze con esponente razionale di α diminuscono all'aumentare dell'esponente, mentre aumentono al diminuire dell'esponente. Quindi, in questo caso, bisogna mettere in F tutti i numeri del tipo αk e quelli minori di essi e nella classe G tutti i numeri del tipo αhe quelli maggiori di essi.
Definizione - Dato un numero reale positivo α minore di 1 ed un numero reale positivo β=(H, K), si chiama potenza di base α ed esponente β, e si indica αβ, il numero reale positivo che rappresenta l'elemento di separazione della sezione di numeri reali, ottenuta ponendo nella classe inferiore F tutti i numeri reali del tipo αk, con k numero razionale di K e tutti quelli minori di essi, e nella classe superiore G tutti i numeri reali del tipo αh, con h numero razionale di H e tutti quelli maggiori di essi. Cioè si pone:
αβ=(F, G).
3° Caso: α>0 e β<0.
In questo caso, tanto per α>1, quanto per 0<α<1, come nel caso degli esponenti razionali, si pone, per definizione:
tenendo presente che, essendo per ipotesi β<0, risulta -β>0, pertanto la potenza α-β è stata definita precedentemente sia per α>1, sia per 0<α<1.
Si completa poi la definizione di potenza reale, ponendo:
1β=1,
quale che sia il numero reale β;
0β=0,
per ogni β>0;
α0=1,
quale che sia il numero reale α.
Non si attribuisce nessun significato alle potenze di base 0 ed esponente negativo o nullo.
Sono state così definite tutte le possibili potenze con base reale positiva ed esponente reale relativo; tutte queste potenze risultano positive.
Nel campo reale non si definisce la potenza di un numero reale negativo con esponente reale.
Alle potenze aventi basi positive ed esponente reale qualsiasi si possono estendere tutti i teoremi dimostrati per le potenze ad esponente razionale. Precisamente, si può dimostrare, e ci si limita solo all'enunciato, che se α, β, γ indicano numeri reali positivi ed r, s, t numeri reali qualsiasi, valgono le seguenti identità:

Si possono anche estendere tutte le altre proprietà dimostrate per le potenze ad esponente razionale; in particolare vale il seguente teorema:
-il valore della potenza di un numero reale maggiore di 1, avente l'esponente reale, aumenta all'aumentare dell'esponente, mentre il valore della potenza di un numero reale positivo minore di 1, diminuisce al diminuire dell'esponente.
quale che sia il numero reale β;
0β=0,
per ogni β>0;
α0=1,
quale che sia il numero reale α.
Non si attribuisce nessun significato alle potenze di base 0 ed esponente negativo o nullo.
Sono state così definite tutte le possibili potenze con base reale positiva ed esponente reale relativo; tutte queste potenze risultano positive.
Nel campo reale non si definisce la potenza di un numero reale negativo con esponente reale.
Alle potenze aventi basi positive ed esponente reale qualsiasi si possono estendere tutti i teoremi dimostrati per le potenze ad esponente razionale. Precisamente, si può dimostrare, e ci si limita solo all'enunciato, che se α, β, γ indicano numeri reali positivi ed r, s, t numeri reali qualsiasi, valgono le seguenti identità:

Si possono anche estendere tutte le altre proprietà dimostrate per le potenze ad esponente razionale; in particolare vale il seguente teorema:
-il valore della potenza di un numero reale maggiore di 1, avente l'esponente reale, aumenta all'aumentare dell'esponente, mentre il valore della potenza di un numero reale positivo minore di 1, diminuisce al diminuire dell'esponente.