MIKY & GENNY
PROGRESSIONI ARITMETICHE E GEOMETRICHE ---> INDICE
Premessa
Una successione indica una classe di numeri in un certo ordine.
Progressioni aritmetiche
Definizione - Una successione di numeri, tali che la differenza tra uno di essi ed il precedente sia costante, tranne il primo se esiste, si dice progressione aritmetica, o per differenza.
La differenza costante si chiama ragione della progressione aritmetica e si indica con la lettera d. I numeri che costituiscono una progressione aritmetica si chiamano termini o elementi della progressione. Per indicare che una successione costituisce una progressione aritmetica, si antepone ad essa il segno ÷.
Esempi
1)-La successione dei numeri interi naturali
÷ 1, 2, 3, 4, 5, 6, ... ,
è una progressione aritmetica di ragione 1.
2)-Le successioni dei numeri pari e quelle dei numeri dispari
÷ 2, 4, 6, 8, 10, 12, ... ,
÷ 1, 3, 5, 7, 9, 11, ... ,
sono progressioni aritmetiche di ragione 2.
3)-Una successione di numeri uguali
÷ 3, 3, 3, 3, 3, 3, ... ,
è una progressione aritmetica di ragione 0.
4)-La successione
÷ 5, 8, 11, 14, 17, 20
è una progressione aritmetica di ragione d=3.
Infatti, si ha:
8-5=3, 11-8=3, 14-11=3, 17-14=3, 20-17=3.
5)-La successione

è una progressione aritmetica di ragione d=-1/2.
Infatti, si ha:

6)-I successivi multipli di kn, con k numero qualsiasi:
0, k, 2k, 3k,, ..., kn, ...
costituiscono una progressione aritmetica di ragione d=k.
Una progressione aritmetica, per il modo in cui è definita, ha infiniti termini e non ha nè il primo nè l'ultimo; perciò dovrà contenere necessariamente tutti i termini positivi e negativi. In seguito saranno considerati il primo e l'ultimo termine di una progressione, o uno dei due, volendo con ciò significare che si tratta di termini della progressione presi in considerazione. Inoltre si dirà che:
-la progressione è limitata se si considera un numero finito di termini,
-la progressione è illimitata se si considerano infiniti termini,
-la progressione è crescente quando ogni termine è maggiore del precedente,
-la progressione è decrescente quando ogni termine è minore del precedente.
÷ 1, 3, 5, 7, 9, 11, ...
Se si considerano nel loro ordine crescente tutti i numeri interi positivi, negativi e lo zero:
÷ ... -3, -2, -1, 0, 1, 2, 3, ... ,
si ottiene una progressione aritmetica illimitata in entrambi i sensi.
Assegnati due termini consecutivi di una progressione aritmetica, a e b nell'ordine, e indicata con d la ragione, per definizione si ha:
b-a=d,
da cui si ricava
(1) a=b-d oppure (2) b=a+d.
Da (1) e (2) segue il seguente teorema:
-in una progressione aritmetica un termine qualsiasi si ottiene dal seguente togliendo la ragione, oppure dal precedente aggiungendola.
Segue quindi che:
-se la ragione di una progressione aritmetica è positiva, la progressione è crescente, ossia ogni termine è maggiore del precedente; se è negativa, la progressione è crescente, ossia ogni termine è minore del precedente; se è nulla, la progressione è costituita da numeri tutti uguali fra loro, e viceversa.
E' anche chiaro che una progressione aritmetica finita, per il teorema precedente, la si può sempre prolungare, nell'uno e nell'altro senso con dei termini, nel numero desiderato, e considerarla parte di una progressione infinita.
Esempio: dalla progressione aritmetica di ragione 4:
2, 6, 10, 14,
si ricava la progressione illimitata nei due sensi
÷ ..., -6, -2, 2, 6, 10, 14, 18, 22, ...,
Una successione indica una classe di numeri in un certo ordine.
Progressioni aritmetiche
Definizione - Una successione di numeri, tali che la differenza tra uno di essi ed il precedente sia costante, tranne il primo se esiste, si dice progressione aritmetica, o per differenza.
La differenza costante si chiama ragione della progressione aritmetica e si indica con la lettera d. I numeri che costituiscono una progressione aritmetica si chiamano termini o elementi della progressione. Per indicare che una successione costituisce una progressione aritmetica, si antepone ad essa il segno ÷.
Esempi
1)-La successione dei numeri interi naturali
÷ 1, 2, 3, 4, 5, 6, ... ,
è una progressione aritmetica di ragione 1.
2)-Le successioni dei numeri pari e quelle dei numeri dispari
÷ 2, 4, 6, 8, 10, 12, ... ,
÷ 1, 3, 5, 7, 9, 11, ... ,
sono progressioni aritmetiche di ragione 2.
3)-Una successione di numeri uguali
÷ 3, 3, 3, 3, 3, 3, ... ,
è una progressione aritmetica di ragione 0.
4)-La successione
÷ 5, 8, 11, 14, 17, 20
è una progressione aritmetica di ragione d=3.
Infatti, si ha:
5)-La successione
è una progressione aritmetica di ragione d=-1/2.
Infatti, si ha:
6)-I successivi multipli di kn, con k numero qualsiasi:
0, k, 2k, 3k,, ..., kn, ...
costituiscono una progressione aritmetica di ragione d=k.
Una progressione aritmetica, per il modo in cui è definita, ha infiniti termini e non ha nè il primo nè l'ultimo; perciò dovrà contenere necessariamente tutti i termini positivi e negativi. In seguito saranno considerati il primo e l'ultimo termine di una progressione, o uno dei due, volendo con ciò significare che si tratta di termini della progressione presi in considerazione. Inoltre si dirà che:
-la progressione è limitata se si considera un numero finito di termini,
-la progressione è illimitata se si considerano infiniti termini,
-la progressione è crescente quando ogni termine è maggiore del precedente,
-la progressione è decrescente quando ogni termine è minore del precedente.
Negli esempi 4) e 5), le progressioni hanno un numero finito di termini, quindi si chiamano progressioni finite.
Un esempio di progressione aritmetica infinita, è dato dai numeri dispari positivi, presi nel loro ordine crescente:
Un esempio di progressione aritmetica infinita, è dato dai numeri dispari positivi, presi nel loro ordine crescente:
÷ 1, 3, 5, 7, 9, 11, ...
Se si considerano nel loro ordine crescente tutti i numeri interi positivi, negativi e lo zero:
÷ ... -3, -2, -1, 0, 1, 2, 3, ... ,
si ottiene una progressione aritmetica illimitata in entrambi i sensi.
Assegnati due termini consecutivi di una progressione aritmetica, a e b nell'ordine, e indicata con d la ragione, per definizione si ha:
b-a=d,
da cui si ricava
(1) a=b-d oppure (2) b=a+d.
Da (1) e (2) segue il seguente teorema:
-in una progressione aritmetica un termine qualsiasi si ottiene dal seguente togliendo la ragione, oppure dal precedente aggiungendola.
Segue quindi che:
-se la ragione di una progressione aritmetica è positiva, la progressione è crescente, ossia ogni termine è maggiore del precedente; se è negativa, la progressione è crescente, ossia ogni termine è minore del precedente; se è nulla, la progressione è costituita da numeri tutti uguali fra loro, e viceversa.
E' anche chiaro che una progressione aritmetica finita, per il teorema precedente, la si può sempre prolungare, nell'uno e nell'altro senso con dei termini, nel numero desiderato, e considerarla parte di una progressione infinita.
Esempio: dalla progressione aritmetica di ragione 4:
2, 6, 10, 14,
si ricava la progressione illimitata nei due sensi
÷ ..., -6, -2, 2, 6, 10, 14, 18, 22, ...,
di cui è parte.
Ennesimo termine di una progressione aritmetica
Si considera ora una progressione aritmetica finita composta da n termini; indicando il primo termine con a1, il secondo con a2, il terzo con a3, ..., l'ennesimo con an, in generale si ha:
a1, a2, a3, ..., an,
di ragione d.
Premesso ciò, si dimostra il seguente teorema:
-in una progressione aritmetica, l'ennesimo termine è uguale al primo aumentato del prodotto della ragione per il numero dei termini che precedono l'ennesimo, cioè:
(1) an=a1+(n-1)d.
Essendo per definizione

sommando membro a membro le n-1 uguaglianze suddette e riducendo i termini simili, si ha:
an - a1=(n-1)d,
cioè
an=a1+(n-1)d.
Dalla formula (1) si ricavano le seguenti formule:

che si applicano per trovare i valori richiesti dai problemi, in funzione di quelli noti.
La formula (1) è valida anche in generale, dimostrando il seguente teorema:
-se ar e as, con r<s, sono due termini qualsiasi di una progressione aritmetica:
(5) as=ar+(s-r)d.
Infatti, per il teorema precedente, si ha:
as=a1+(s-1)d e ar=a1+(r-1)d.
Sottraendo membro a membro, si ha:
as-ar=a1+(s-1)d-a1-(r-1)d,
ossia
as-ar=(s-r)d,
quindi
as=ar+(s-r)d,
come volevasi dimostrare.
Esempi
1)-In una progressione aritmetica il primo termine è uguale a -8, la ragione d=7, trovare il quinto termine.
Si applica la formula an=a1+(n-1)d, ponendo in essa n=5, a1=-8, e d=7. Pertanto risulta:
a5=-8+28=20.
2)-In una progressione aritmetica il quinto termine è uguale a 38, la ragione d=3, trovare il dodicesimo termine.
Si applica la formula as=ar+(s-r)d, ponendo in essa s=12, r=5, ar=38, e d=3. Pertanto risulta:
a12=-38+21=59.
3)-In una progressione aritmetica il terzo termine è uguale a 23 ed il nono uguale a 11, trovare la ragione.
Si applica la formula as=ar+(s-r)d, ponendo in essa s=9, r=3, ar=23, e as=11. Pertanto si ha:
11=23+6d,
da cui
4)-in una progressione aritmetica, di ragione 1/3, il primo termine è uguale a 9 e l'ultimo uguale a 34/3, trovare il numero dei termini.
Si applica la formula an=a1+(n-1)d, ponendo in essa a1=9, an=34/3 e d=1/3. Pertanto risulta:
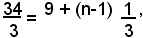
da cui si ricava
n-1=7,
cioè
n=8.
Nota beneL'esempio (4) non è sempre possibile, perchè il numero n deve risultare intero e positivo.
Esempio: trovare il numero dei termini di una progressione aritmetica di ragione 6 avente il primo termine uguale a 36 e l'ultimo uguale a 9.
Si applica la formula an=a1+(n-1)d, ponendo in essa a1=9, an=36 e d=6. Pertanto risulta:
36=9 + 6(n-1),
da cui si ricava
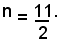
Tale valore non è accettabile e quindi il problema è impossibile.
Inserimento di medi aritmetici fra due numeri assegnati
Inserire fra due numeri, a e b, m medi aritmetici, significa formare una progressione aritmetica di m+2 termini nella quale a e b siano, rispettivamente, il primo e l'ultimo.
A tale scopo, per scrivere i termini intermedi fra a e b, basta conoscere la ragione. Questa è data dalla formula (3) suddetta, ponendo in essa b=an, a=a1 e m+2=n, quindi risulta: (6)

e la progressione è
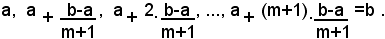
Esempio: inserire fra i numeri 7 e 28 altri 6 numeri formanti con essi una progressione aritmetica.
Ponendo nella (6) a=7, b=28, m=6, si ha:
d=3
e quindi la progressione
7, 10, 13, 16, 19, 22, 25, 28.
Definizione - In una progressione aritmetica finita, di termini estremi a e b, due termini f e g si dicono equidistanti dagli estremi quando il numero dei termini della progressione, che vanno da a ad f, è uguale al numero dei termini che vanno da g a b.
Considerata la progressione aritmetica:
3, 8, 13, 18, 23, 28, 33, 38,
la somma di due termini qualsiasi equidistanti dagli estremi è uguale alla somma dei termini estremi. Infatti:
3+38=41, 8+33=41, 13+28=41, 18+23=41.
L'esempio suddetto è valido in generale, pertanto si dimostra il seguente teorema:
-in una progressione aritmetica finita, la somma di due termini equidistanti dai due termini estremi è uguale alla somma dei due termini estremi.
Indicati con a e b i termini estremi della progressione e con f e g due termini equidistanti dagli estremi, si dimostra che:
f+g=a+b.
A tale scopo, se si indica con r il numero dei termini della progressione che vanno da a ad f, r sarà pure il numero dei termini che vanno da g a b.
Ponendo n=r nella formula an=a1+(n-1)d, si ha:
f=a+(r-1)d, b=g+(r-1)d,
da cui, sottraendo membro a membro, dalla prima uguaglianza la seconda, si ottiene
f-b=a-g,
ossia
f+g=a+b,
come volevasi dimostrare.
Somma dei termini consecutivi di una progressione aritmetica
Data la progressione aritmetica di n termini:
a1, a2, a3, ..., an-2, an-1, an,
si può trovare una regola per calcolare la somma Sn dei suoi n termini, senza conoscerli tutti.
Teorema - La somma dei primi n termini consecutivi di una progressione aritmetica è uguale alla semisomma dei termini estremi moltiplicata per il numero n dei termini, cioè:

Infatti, la somma Sn dei suoi n termini è:
che per la proprietà commutativa dell'addizione si può scrivere
Sommando membro a membro le due uguaglianze suddette e applicando la proprietà associativa dell'addizione, si ha:
Per il teorema precedentemente dimostrato, le somme indicate nelle varie parentesi sono tutte uguali alla prima di esse, perchè somme di termini equidistanti dai termini estremi, quindi la somma di esse è uguale a (a1 + an)n e si può scrivere:
2Sn = (a1 + an)n,
da cui si ricava

Il teorema è così dimostrato.
Tale formula permette di calcolare la somma di n termini consecutivi di una progressione aritmetica, conoscendo il numero n di termini che si devono addizionare ed inoltre il primo e l'ultimo termine. Siccome l'ultimo termine, per la formula an=a1+(n-1)d, si può calcolare conoscendo il primo termine, la ragione ed il numero dei termini, la somma può calcolarsi quando sono assegnati il primo termine, la ragione ed il numero dei termini.
Esempi
1)-Calcolare la somma dei primi sette termini di una progressione aritmetica il cui primo termine è uguale ad -8 e la ragione 5.
Ponendo a1=-8, d=5, n=7 nella formula an=a1+(n-1)d, si ha:
a7=-8+30=22.
Quindi si ricava:
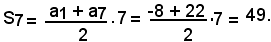
Nota bene
Le formule: (1)
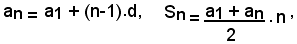
permettono di risolvere tutti i problemi sulle progressione aritmetiche, quando dei cinque numeri a1, an, n, d, Sn, se ne conoscono tre, perchè in tal caso si ottiene un sistema di due equazioni in due incognite, che è al massimo di secondo grado.
Esempi
1)-In una progressione aritmetica il primo termine è uguale a 2, l'ultimo uguale a 20 e la somma di tutti i termini è uguale a 77. Determinare il numero dei termini e la ragione della progressione.
Ponendo a1=2, an=20, Sn=77 nelle formule (1) suddette, si ha il seguente sistema nelle incognite n e d:

Dalla seconda equazione si ricava n=7 e, sostituendo tale valore nella prima, si ottiene d=3.
2)-In una progressione aritmetica il primo termine è uguale a 5, la ragione uguale a 2 e la somma dei primi n termini è uguale a 117. Determinare il numero dei termini e l'ultimo termine.
Ponendo a1=5, d=2, Sn=117 nelle formule (1) suddette, si ha il seguente sistema nelle incognite n e an:

3)-La somma di tre numeri di una progressione aritmetica è uguale a 15/12, mentre la somma dei loro reciproci è uguale a 37/30. Trovare i tre numeri.
Si indica con x il secondo dei tre numeri cercati e con y la ragione della progressione aritmetica. Il primo numero è allora uguale a x-y e il terzo uguale a x+y. Per le condizioni date dal problema, si può scrivere il seguente sistema:

Dalla prima equazione si ricava x=5/2 e, sostituendo tale valore nella seconda, dopo facili semplificazioni si ottiene l'equazione:
4y2=1,
le cui radici sono:

I tre numeri cercati sono quindi:

Progressioni geometriche
Definizione - Una successione di numeri, tali che il quoziente tra uno di essi ed il precedente sia costante, tranne il primo se esiste, si dice progressione geometrica o per quoziente.
Il quoziente costante tra ogni numero ed il precedente si chiama ragione della progressione geometrica e si indica con la lettera q. I numeri che costituiscono una progressione geometrica si chiamano termini o elementi della progressione. Per indicare che una successione costituisce una progressione geometrica, si antepone ad essa il segno ÷÷.
Esempi di progressioni geometriche finite, cioè aventi un numero finito di termini, sono:
÷÷ 5, 10, 20, 40, 80, 160;

di ragione, rispettivamente, 2 e -1/2.
Esempi di progressioni geometriche composte da infiniti termini, e illimitatamente estese in un solo senso, sono:
÷÷ 1, -2, 4, -8, 16, ...,

di ragione, rispettivamente, -2 e -1/3.
Esempio di progressione geometrica illimitatamente estesa nei due sensi, è:
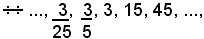
di ragione 5.
Nota bene
In virtù della definizione di progressione geometrica, nessun termine pùo essere nullo, quindi anche la ragione dev'essere sempre diversa da zero.
Se a e b sono due termini consecutivi di una progressione geometrica e q la ragione, per definizione si ha:

Da (1) e (2) segue il seguente teorema:
-in una progressione geometrica, un termine qualsiasi si ottiene dal seguente dividendolo per la ragione, oppure dal precedente, moltiplicandolo.
Da tale teorema segue:
-se la ragione è positiva, i termini della progressione geometrica sono di segno uguale, tutti positivi o tutti negativi,
-se la ragione è negativa, i termini della progressione geometrica sono alternativamente uno positivo ed uno negativo,
-se in una progressione geometrica a termini positivi, la ragione è un numero positivo maggiore di 1, la progressione è crescente, cioè ogni termine è maggiore del precedente,
-se la ragione è un numero positivo minore di 1, la progressione è decrescente, cioè ogni termine è minore del precedente.
Dal teorema suddetto segue anche che una progressione geometrica finita la si può prolungare dei termini desiderati, sia nell'uno che nell'altro senso, e considerarla parte di una progressione infinita.
Ad esempio, dalla progressione geometrica di ragione 2:
÷÷ 3, 6, 12, 24,
si ricava la progressione geometrica illimitata nei due sensi

Ennesimo termine di una progressione geometrica finita
Assegnata la progressione geometrica finita
÷÷ a1, a2, a3, ..., an-1, an,
di ragione q, si dimostra il seguente teorema:
-l'ennesimo termine di una progressione geometrica finita è uguale al primo termine moltiplicato per la ragione elevata ad un esponente uguale al numero dei termini che precedono l'ennesimo, cioè: (3)

Essendo per definizione

moltiplicando membro a membro le n-1 uguaglianze suddette e semplificando i prodotti ottenuti, si ha:

ossia

Ciò è quanto si voleva dimostrare.
La formula (3) si può generalizzare dimostrando il seguente teorema:
-se ar e as, con r<s, sono due termini qualsiasi di una progressione geometica, risulta: (4)

Infatti, per il teorema precedente, si ha:

Dividendo membro a membro queste due uguaglianze, si ottiene:
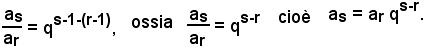
Ciò è quanto si voleva dimostrare.
Esempi
1)-In una progressione geometrica il primo termine è 3 e la ragione 2. Trovare il quinto termine.
Si applica la formula (3), ponendo in essa a1=3, n=5, q=2. Pertanto risulta:
a5=3(2)4=48.
2)-In una progressione geometrica il settimo termine è 81 e la ragione 3. Trovare il primo termine.
Si applica la formula (3), ponendo in essa a7=81, n=7, q=3. Pertanto risulta:
81 = a1(3)6,
da cui si ricava

3)-In una progressione geometrica il quarto termine è 15 e la ragione 1/3. Trovare l'ottavo termine.
Si applica la formula (4), ponendo in essa r=4, s=8, q=1/3. Pertanto risulta:

4)-In una progressione geometrica il secondo termine è 6 ed il sesto 32/27. Trovare la ragione.
Si applica la formula (4), ponendo in essa r=2, s=6, q=32/27. Pertanto si ha:

da cui si ricava (5)

Nota bene
La determinazione del numero n dei termini di una progressione geometrica, conduce ad un'equazione in cui l'incognita n figura all'esponente di una potenza: questo tipo di equazione sarà trattata in seguito.
Inserimento di medi geometrici fra due numeri assegnati
Inserire fra due numeri, a e b, m medi geometrici, significa formare una progressione geometrica di m+2 termini nella quale a e b sono, rispettivamente, il primo e l'ultimo.
A tale scopo, per scrivere i termini intermedi fra a e b, basta conoscere la ragione. Questa si ricava dalla formula (3) suddetta, ponendo in essa b=an, a=a1 e m=n, quindi risulta: (6)
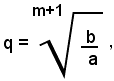
Da tale uguaglianza si vede che:
-se p è un numero pari e quindi p+1 dispari, si ricava un solo valore di q, quale che sia il numero b/a,
-se p è un numero dispari e quindi p+1 è pari, si ricavano due valori di q fra loro opposti se il suo numero (b/a)>0,
-se (a/b) >0, non si ricava alcun valore.
Ennesimo termine di una progressione aritmetica
Si considera ora una progressione aritmetica finita composta da n termini; indicando il primo termine con a1, il secondo con a2, il terzo con a3, ..., l'ennesimo con an, in generale si ha:
a1, a2, a3, ..., an,
di ragione d.
Premesso ciò, si dimostra il seguente teorema:
-in una progressione aritmetica, l'ennesimo termine è uguale al primo aumentato del prodotto della ragione per il numero dei termini che precedono l'ennesimo, cioè:
(1) an=a1+(n-1)d.
Essendo per definizione

sommando membro a membro le n-1 uguaglianze suddette e riducendo i termini simili, si ha:
cioè
Dalla formula (1) si ricavano le seguenti formule:
che si applicano per trovare i valori richiesti dai problemi, in funzione di quelli noti.
La formula (1) è valida anche in generale, dimostrando il seguente teorema:
-se ar e as, con r<s, sono due termini qualsiasi di una progressione aritmetica:
(5) as=ar+(s-r)d.
Infatti, per il teorema precedente, si ha:
as=a1+(s-1)d e ar=a1+(r-1)d.
Sottraendo membro a membro, si ha:
as-ar=a1+(s-1)d-a1-(r-1)d,
ossia
as-ar=(s-r)d,
quindi
as=ar+(s-r)d,
come volevasi dimostrare.
Esempi
1)-In una progressione aritmetica il primo termine è uguale a -8, la ragione d=7, trovare il quinto termine.
Si applica la formula an=a1+(n-1)d, ponendo in essa n=5, a1=-8, e d=7. Pertanto risulta:
a5=-8+28=20.
2)-In una progressione aritmetica il quinto termine è uguale a 38, la ragione d=3, trovare il dodicesimo termine.
Si applica la formula as=ar+(s-r)d, ponendo in essa s=12, r=5, ar=38, e d=3. Pertanto risulta:
a12=-38+21=59.
3)-In una progressione aritmetica il terzo termine è uguale a 23 ed il nono uguale a 11, trovare la ragione.
Si applica la formula as=ar+(s-r)d, ponendo in essa s=9, r=3, ar=23, e as=11. Pertanto si ha:
11=23+6d,
da cui
d=-2.
4)-in una progressione aritmetica, di ragione 1/3, il primo termine è uguale a 9 e l'ultimo uguale a 34/3, trovare il numero dei termini.
Si applica la formula an=a1+(n-1)d, ponendo in essa a1=9, an=34/3 e d=1/3. Pertanto risulta:
da cui si ricava
n-1=7,
cioè
n=8.
Nota bene
Esempio: trovare il numero dei termini di una progressione aritmetica di ragione 6 avente il primo termine uguale a 36 e l'ultimo uguale a 9.
Si applica la formula an=a1+(n-1)d, ponendo in essa a1=9, an=36 e d=6. Pertanto risulta:
da cui si ricava
Tale valore non è accettabile e quindi il problema è impossibile.
Inserimento di medi aritmetici fra due numeri assegnati
Inserire fra due numeri, a e b, m medi aritmetici, significa formare una progressione aritmetica di m+2 termini nella quale a e b siano, rispettivamente, il primo e l'ultimo.
A tale scopo, per scrivere i termini intermedi fra a e b, basta conoscere la ragione. Questa è data dalla formula (3) suddetta, ponendo in essa b=an, a=a1 e m+2=n, quindi risulta: (6)
e la progressione è
Esempio: inserire fra i numeri 7 e 28 altri 6 numeri formanti con essi una progressione aritmetica.
Ponendo nella (6) a=7, b=28, m=6, si ha:
e quindi la progressione
7, 10, 13, 16, 19, 22, 25, 28.
Definizione - In una progressione aritmetica finita, di termini estremi a e b, due termini f e g si dicono equidistanti dagli estremi quando il numero dei termini della progressione, che vanno da a ad f, è uguale al numero dei termini che vanno da g a b.
Considerata la progressione aritmetica:
3, 8, 13, 18, 23, 28, 33, 38,
la somma di due termini qualsiasi equidistanti dagli estremi è uguale alla somma dei termini estremi. Infatti:
L'esempio suddetto è valido in generale, pertanto si dimostra il seguente teorema:
-in una progressione aritmetica finita, la somma di due termini equidistanti dai due termini estremi è uguale alla somma dei due termini estremi.
Indicati con a e b i termini estremi della progressione e con f e g due termini equidistanti dagli estremi, si dimostra che:
f+g=a+b.
A tale scopo, se si indica con r il numero dei termini della progressione che vanno da a ad f, r sarà pure il numero dei termini che vanno da g a b.
Ponendo n=r nella formula an=a1+(n-1)d, si ha:
da cui, sottraendo membro a membro, dalla prima uguaglianza la seconda, si ottiene
ossia
f+g=a+b,
come volevasi dimostrare.
Somma dei termini consecutivi di una progressione aritmetica
Data la progressione aritmetica di n termini:
a1, a2, a3, ..., an-2, an-1, an,
si può trovare una regola per calcolare la somma Sn dei suoi n termini, senza conoscerli tutti.
Teorema - La somma dei primi n termini consecutivi di una progressione aritmetica è uguale alla semisomma dei termini estremi moltiplicata per il numero n dei termini, cioè:
Infatti, la somma Sn dei suoi n termini è:
Sn = a1 + a2 + a3 + ... + an-2 + an-1 + an,
che per la proprietà commutativa dell'addizione si può scrivere
Sn = an + an-1 + an-2 + a3 + ... + a2 + a1.
Sommando membro a membro le due uguaglianze suddette e applicando la proprietà associativa dell'addizione, si ha:
2Sn = (a1 + an) + (a2 + an-1) + (a3 + an-2) + ... + (an-1 + a2) + (an + a1).
Per il teorema precedentemente dimostrato, le somme indicate nelle varie parentesi sono tutte uguali alla prima di esse, perchè somme di termini equidistanti dai termini estremi, quindi la somma di esse è uguale a (a1 + an)n e si può scrivere:
2Sn = (a1 + an)n,
da cui si ricava
Il teorema è così dimostrato.
Tale formula permette di calcolare la somma di n termini consecutivi di una progressione aritmetica, conoscendo il numero n di termini che si devono addizionare ed inoltre il primo e l'ultimo termine. Siccome l'ultimo termine, per la formula an=a1+(n-1)d, si può calcolare conoscendo il primo termine, la ragione ed il numero dei termini, la somma può calcolarsi quando sono assegnati il primo termine, la ragione ed il numero dei termini.
Esempi
1)-Calcolare la somma dei primi sette termini di una progressione aritmetica il cui primo termine è uguale ad -8 e la ragione 5.
Ponendo a1=-8, d=5, n=7 nella formula an=a1+(n-1)d, si ha:
Quindi si ricava:
Nota bene
Le formule: (1)
permettono di risolvere tutti i problemi sulle progressione aritmetiche, quando dei cinque numeri a1, an, n, d, Sn, se ne conoscono tre, perchè in tal caso si ottiene un sistema di due equazioni in due incognite, che è al massimo di secondo grado.
Esempi
1)-In una progressione aritmetica il primo termine è uguale a 2, l'ultimo uguale a 20 e la somma di tutti i termini è uguale a 77. Determinare il numero dei termini e la ragione della progressione.
Ponendo a1=2, an=20, Sn=77 nelle formule (1) suddette, si ha il seguente sistema nelle incognite n e d:

Dalla seconda equazione si ricava n=7 e, sostituendo tale valore nella prima, si ottiene d=3.
2)-In una progressione aritmetica il primo termine è uguale a 5, la ragione uguale a 2 e la somma dei primi n termini è uguale a 117. Determinare il numero dei termini e l'ultimo termine.
Ponendo a1=5, d=2, Sn=117 nelle formule (1) suddette, si ha il seguente sistema nelle incognite n e an:

Sostituendo nella seconda equazione il valore di an, dato dalla prima equazione, dopo facili semplificazioni, si ottiene l'equazione di secondo grado nell'incognita n:
n2 + 4n - 117 =0 ,
le cui radici sono 9 e -13.
Siccome n dev'essere positivo, si esclude il valore -13 e, sostituendo il valore 9 nella prima equazione, si ricava:
an = 5 + 16 = 21 .
La progressione è quindi di 9 termini e l'ultimo termine, il nono, è 21.
n2 + 4n - 117 =0 ,
le cui radici sono 9 e -13.
Siccome n dev'essere positivo, si esclude il valore -13 e, sostituendo il valore 9 nella prima equazione, si ricava:
an = 5 + 16 = 21 .
La progressione è quindi di 9 termini e l'ultimo termine, il nono, è 21.
3)-La somma di tre numeri di una progressione aritmetica è uguale a 15/12, mentre la somma dei loro reciproci è uguale a 37/30. Trovare i tre numeri.
Si indica con x il secondo dei tre numeri cercati e con y la ragione della progressione aritmetica. Il primo numero è allora uguale a x-y e il terzo uguale a x+y. Per le condizioni date dal problema, si può scrivere il seguente sistema:

Dalla prima equazione si ricava x=5/2 e, sostituendo tale valore nella seconda, dopo facili semplificazioni si ottiene l'equazione:
4y2=1,
le cui radici sono:
I tre numeri cercati sono quindi:
Progressioni geometriche
Definizione - Una successione di numeri, tali che il quoziente tra uno di essi ed il precedente sia costante, tranne il primo se esiste, si dice progressione geometrica o per quoziente.
Il quoziente costante tra ogni numero ed il precedente si chiama ragione della progressione geometrica e si indica con la lettera q. I numeri che costituiscono una progressione geometrica si chiamano termini o elementi della progressione. Per indicare che una successione costituisce una progressione geometrica, si antepone ad essa il segno ÷÷.
Esempi di progressioni geometriche finite, cioè aventi un numero finito di termini, sono:
÷÷ 5, 10, 20, 40, 80, 160;
di ragione, rispettivamente, 2 e -1/2.
Esempi di progressioni geometriche composte da infiniti termini, e illimitatamente estese in un solo senso, sono:
÷÷ 1, -2, 4, -8, 16, ...,
di ragione, rispettivamente, -2 e -1/3.
Esempio di progressione geometrica illimitatamente estesa nei due sensi, è:
di ragione 5.
Nota bene
In virtù della definizione di progressione geometrica, nessun termine pùo essere nullo, quindi anche la ragione dev'essere sempre diversa da zero.
Se a e b sono due termini consecutivi di una progressione geometrica e q la ragione, per definizione si ha:
Da (1) e (2) segue il seguente teorema:
-in una progressione geometrica, un termine qualsiasi si ottiene dal seguente dividendolo per la ragione, oppure dal precedente, moltiplicandolo.
Da tale teorema segue:
-se la ragione è positiva, i termini della progressione geometrica sono di segno uguale, tutti positivi o tutti negativi,
-se la ragione è negativa, i termini della progressione geometrica sono alternativamente uno positivo ed uno negativo,
-se in una progressione geometrica a termini positivi, la ragione è un numero positivo maggiore di 1, la progressione è crescente, cioè ogni termine è maggiore del precedente,
-se la ragione è un numero positivo minore di 1, la progressione è decrescente, cioè ogni termine è minore del precedente.
Dal teorema suddetto segue anche che una progressione geometrica finita la si può prolungare dei termini desiderati, sia nell'uno che nell'altro senso, e considerarla parte di una progressione infinita.
Ad esempio, dalla progressione geometrica di ragione 2:
÷÷ 3, 6, 12, 24,
si ricava la progressione geometrica illimitata nei due sensi
Ennesimo termine di una progressione geometrica finita
Assegnata la progressione geometrica finita
÷÷ a1, a2, a3, ..., an-1, an,
di ragione q, si dimostra il seguente teorema:
-l'ennesimo termine di una progressione geometrica finita è uguale al primo termine moltiplicato per la ragione elevata ad un esponente uguale al numero dei termini che precedono l'ennesimo, cioè: (3)
Essendo per definizione

moltiplicando membro a membro le n-1 uguaglianze suddette e semplificando i prodotti ottenuti, si ha:

ossia
Ciò è quanto si voleva dimostrare.
La formula (3) si può generalizzare dimostrando il seguente teorema:
-se ar e as, con r<s, sono due termini qualsiasi di una progressione geometica, risulta: (4)
Infatti, per il teorema precedente, si ha:
Dividendo membro a membro queste due uguaglianze, si ottiene:
Ciò è quanto si voleva dimostrare.
Esempi
1)-In una progressione geometrica il primo termine è 3 e la ragione 2. Trovare il quinto termine.
Si applica la formula (3), ponendo in essa a1=3, n=5, q=2. Pertanto risulta:
a5=3(2)4=48.
2)-In una progressione geometrica il settimo termine è 81 e la ragione 3. Trovare il primo termine.
Si applica la formula (3), ponendo in essa a7=81, n=7, q=3. Pertanto risulta:
81 = a1(3)6,
da cui si ricava
3)-In una progressione geometrica il quarto termine è 15 e la ragione 1/3. Trovare l'ottavo termine.
Si applica la formula (4), ponendo in essa r=4, s=8, q=1/3. Pertanto risulta:

4)-In una progressione geometrica il secondo termine è 6 ed il sesto 32/27. Trovare la ragione.
Si applica la formula (4), ponendo in essa r=2, s=6, q=32/27. Pertanto si ha:
da cui si ricava (5)

Nota bene
La determinazione del numero n dei termini di una progressione geometrica, conduce ad un'equazione in cui l'incognita n figura all'esponente di una potenza: questo tipo di equazione sarà trattata in seguito.
Inserimento di medi geometrici fra due numeri assegnati
Inserire fra due numeri, a e b, m medi geometrici, significa formare una progressione geometrica di m+2 termini nella quale a e b sono, rispettivamente, il primo e l'ultimo.
A tale scopo, per scrivere i termini intermedi fra a e b, basta conoscere la ragione. Questa si ricava dalla formula (3) suddetta, ponendo in essa b=an, a=a1 e m=n, quindi risulta: (6)
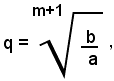
Da tale uguaglianza si vede che:
-se p è un numero pari e quindi p+1 dispari, si ricava un solo valore di q, quale che sia il numero b/a,
-se p è un numero dispari e quindi p+1 è pari, si ricavano due valori di q fra loro opposti se il suo numero (b/a)>0,
-se (a/b) >0, non si ricava alcun valore.
Quindi,
trovata, se è possibile, la ragione q, si calcolano
facilmente i numeri da inserire fra a e b. La progressione
risulta:

Esempio: inserire fra i numeri 5 e 405 tre medi geometrici.
Si ha:

I numeri da inserire fra 5 e 405. sono:
15, 45, 135,
oppure
-15, -45, -135 .
Teorema - In una progressione geometrica finita il prodotto di due termini equidistanti dai due termini estremi è uguale al prodotto degli stessi.
Indicati con a e b i termini estremi della progressione geometrica, e con f e g due termini equidistanti dagli estremi, si tratta di dimostrare che risulta:
fg=ab.
A tale scopo, se si indica con r il numero dei termini della progressione che vanno da a ad f, sarà anche r il numero dei termini che vanno da g a b e, per la formula (3), ponendo in essa n=r, si ha:
f=aqr-1, b=gqr-1,
da cui, dividendo membro a membro, si ottiene
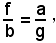
Prodotto di termini consecutivi di una progressione geometrica
Data la progressione geometrica di n termini positivi:
÷÷ a1, a2, a3, ..., an-2, an-1, an,
si vuole calcolare il prodotto Pn dei suoi n termini.
Teorema - Il prodotto dei primi n termini di una progressione geometrica a termini positivi, è uguale alla radice quadrata di una potenza avente per base il prodotto dei termini estremi e per esponente il numero n dei termini della progressione, cioè: (7)

Infatti, risulta:
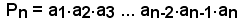
che, per la proprietà commutativa della moltiplicazione, si può scrivere

Moltiplicando membro a membro le due uguaglianze suddette ed applicando la proprietà associativa della moltiplicazione, si ha:
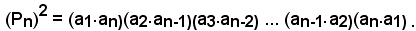
Per il teorema dimostrato in precedenza, i prodotti indicati nelle varie parentesi sono tutti uguali al primo di essi, quindi il loro prodotto è uguale a:

e si può scrivere
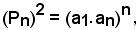
da cui si ricava

Ciò è quanto si voleva dimostrare.
Esempio: calcolare il prodotto dei primi sei termini di una progressione geometrica il cui primo termine è 24 e la ragione 1/2.

Nota bene
Se i termini della progressione geometrica non sono tutti positivi, allora il secondo membro della formula (7) dà il valore assoluto del prodotto di questi termini. In questo caso perciò la formula (7) va sostituita con la seguente:

Il segno del prodotto viene poi deciso caso per caso.
Somma di termini consecutivi di una progressione geometrica
Data la progressione geometrica di n termini positivi:
÷÷ a1, a2, a3, ..., an-2, an-1, an,
si vuole calcolare la somma Sn dei suoi n termini.
Teorema - La somma di n termini consecutivi di una progressione geometrica, la cui ragione sia diversa da uno, si ottiene moltiplicando il primo termine per una frazione, il cui numeratore è la differenza fra l'unità e la ragione elevata al numero n dei termini, mentre il denominatore è la differenza fra l'unità e la ragione, cioè: (8)

Infatti, posto
e moltiplicando ambo i membri di questa uguaglianza per la ragione q. si ha:
(10) qSn = a1q + a2q + a3q + ... + an-2q + an-1q + anq .
Siccome per un teorema precedente un termine qualsiasi si ottiene dal precedente moltiplicandolo per la ragione, o dal seguente dividendolo, si ha:
a1q=a2, a2q=a3, ... an-2q=an-1 + an-1q=an,
ed essendo
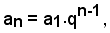
risulta

pertanto la (10) si può scrivere sotto la forma
(11) qSn = a2 + a3 + ... + an-1 + an + a1qn .
Sottraendo membro a membro dalla (8) la (10), si ottiene:
Sn - qSn = (a1 + a2 + a3 + ... + an-1 + an) - (a2 + a3 + ... + an-1 + an + a1qn),
ossia, dopo facili semplificazioni
Sn (1-q) = 1 - qn .
Siccome la ragione q≠1, si ricava:

Ciò è quanto si voleva dimostrare.
Esempi
1)-Calcolare la somma dei primi 5 termini di una progressione geometrica il cui primo termine è uguale a 2 e la ragione uguale a 3.
Essendo a1=2, q=3, applicando la formula (8), si ha:

2)-Una progressione geometrica di ragione 2 è formata da tre termini la cui somma è 63. Trovare i termini della progressione.
Essendo q=2, S3=63, applicando la formula (8), si ha:

Da tal formula si ricava a1=9, quindi i termini della progressione sono 9, 18, 36.
3)-In una progressione geometrica la somma di tre numeri positivi è uguale a 52 e la differenza tra il secondo ed il primo numero è uguale ad 8. Trovare i tre numeri.
Indicando con x il secondo numero e con y la ragione, i tre numeri incogniti sono rappresentati da x/y, x, xy e, tenendo conto dei dati del problema, si può scrivere il sistema:

ossia, eliminando i denominatori (1)

Dividendo membro a membro le due equazioni, si ottiene l'equazione:

la cui forma intera è:
2y2 -11y+15=0
e ammette le radici y1=3, y2=5/2.
Sostituendo i valori trovati al posto della y, nella seconda equazione del sistema (1) si ricava, rispettivamente, x1=12, x2=40/3. I tre numeri cercati, sono:
4, 12, 36,
oppure

Tipi di medie
Media aritmetica
Definizione - Dicesi media aritmetica di n numeri la loro somma divisa per n.
Se si indicano con:
a1 + a2 + ... +an,
gli n numeri e con ma la loro media arirtmetica, per definizione, si ha:

La media aritmetica dei quattro numeri 5, -8, 7, 11, è data da:

Media ponderata
Se si indicano ora con:p1, p2, ... pn,
r numeri interi positivi e si suppone di avere p1 numeri uguali al numero a1, p2 numeri uguali al numero a2, pr numeri uguali al numero a. La media aritmetica di tutti questi numeri, in base alla definizione data è uguale a:

che si può anche scrivere sotto la forma
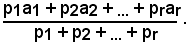
Il valore di tale rapporto si chiama media ponderata dei numeri a1, a2 , ..., ar ed i numeri interi positivi p1, p2, ..., pr si chiamano rispettivamente pesi dei numeri a1, a2 ,..., ar.
Definizione - Si chiama media ponderata dei numeri a1, a2, ..., ar, di pesi rispettivamente p1, p2, ..., pr, la somma dei prodotti di questi numeri per i rispettivi pesi divisa per la somma dei pesi, cioè:

Esempio: trovare la media ponderata dei numeri 3/5, -4, 9, di pesi rispettivamente 15, 2, 3.
Si ha:

Media geometrica
Definizione - Si chiama media geometrica di n numeri positivi a1, a2, ..., an, la radice ennesima aritmetica del loro prodotto, cioè:

Esempio: trovare la media geometrica dei numeri 3, 18, 2, 12.
Si ha:
Media armonicaDefinizione - Si chiama media armonica di n numeri a1, a2, ..., an, non nulli, il reciproco della media aritmetica dei reciproci dei numeri dati, cioè:

Esempio: trovare la media armonica dei numeri 2, 2/3, 3.
Si ha:

Nota bene
Se gli n numeri a1, a2, ..., an, sono tutti uguali fra loro e sono tutti positivi, allora la loro media aritmetica e la loro media armonica coincidono con il valore comune di uno qualsiasi di essi. Se invece i numeri a1, a2, ..., an, sono positivi e non tutti uguali, allora si può dimostrare che:
-la media aritmetica è maggiore della media geometrica e quest'ultima è maggiore di quella armonica.

Esempio: inserire fra i numeri 5 e 405 tre medi geometrici.
Si ha:

I numeri da inserire fra 5 e 405. sono:
15, 45, 135,
oppure
-15, -45, -135 .
Teorema - In una progressione geometrica finita il prodotto di due termini equidistanti dai due termini estremi è uguale al prodotto degli stessi.
Indicati con a e b i termini estremi della progressione geometrica, e con f e g due termini equidistanti dagli estremi, si tratta di dimostrare che risulta:
A tale scopo, se si indica con r il numero dei termini della progressione che vanno da a ad f, sarà anche r il numero dei termini che vanno da g a b e, per la formula (3), ponendo in essa n=r, si ha:
da cui, dividendo membro a membro, si ottiene
ossia
fg=ab,
come volevasi dimostrare.
fg=ab,
come volevasi dimostrare.
Prodotto di termini consecutivi di una progressione geometrica
Data la progressione geometrica di n termini positivi:
÷÷ a1, a2, a3, ..., an-2, an-1, an,
si vuole calcolare il prodotto Pn dei suoi n termini.
Teorema - Il prodotto dei primi n termini di una progressione geometrica a termini positivi, è uguale alla radice quadrata di una potenza avente per base il prodotto dei termini estremi e per esponente il numero n dei termini della progressione, cioè: (7)
Infatti, risulta:
che, per la proprietà commutativa della moltiplicazione, si può scrivere
Moltiplicando membro a membro le due uguaglianze suddette ed applicando la proprietà associativa della moltiplicazione, si ha:
Per il teorema dimostrato in precedenza, i prodotti indicati nelle varie parentesi sono tutti uguali al primo di essi, quindi il loro prodotto è uguale a:
e si può scrivere
da cui si ricava
Ciò è quanto si voleva dimostrare.
Esempio: calcolare il prodotto dei primi sei termini di una progressione geometrica il cui primo termine è 24 e la ragione 1/2.

Nota bene
Se i termini della progressione geometrica non sono tutti positivi, allora il secondo membro della formula (7) dà il valore assoluto del prodotto di questi termini. In questo caso perciò la formula (7) va sostituita con la seguente:
Il segno del prodotto viene poi deciso caso per caso.
Somma di termini consecutivi di una progressione geometrica
Data la progressione geometrica di n termini positivi:
÷÷ a1, a2, a3, ..., an-2, an-1, an,
si vuole calcolare la somma Sn dei suoi n termini.
Teorema - La somma di n termini consecutivi di una progressione geometrica, la cui ragione sia diversa da uno, si ottiene moltiplicando il primo termine per una frazione, il cui numeratore è la differenza fra l'unità e la ragione elevata al numero n dei termini, mentre il denominatore è la differenza fra l'unità e la ragione, cioè: (8)

Infatti, posto
(9) Sn = a1 + a2 + a3 + ... + an-2 + an-1 + an
e moltiplicando ambo i membri di questa uguaglianza per la ragione q. si ha:
(10) qSn = a1q + a2q + a3q + ... + an-2q + an-1q + anq .
Siccome per un teorema precedente un termine qualsiasi si ottiene dal precedente moltiplicandolo per la ragione, o dal seguente dividendolo, si ha:
a1q=a2, a2q=a3, ... an-2q=an-1 + an-1q=an,
ed essendo
risulta
pertanto la (10) si può scrivere sotto la forma
(11) qSn = a2 + a3 + ... + an-1 + an + a1qn .
Sottraendo membro a membro dalla (8) la (10), si ottiene:
Sn - qSn = (a1 + a2 + a3 + ... + an-1 + an) - (a2 + a3 + ... + an-1 + an + a1qn),
ossia, dopo facili semplificazioni
Sn (1-q) = 1 - qn .
Siccome la ragione q≠1, si ricava:

Ciò è quanto si voleva dimostrare.
Esempi
1)-Calcolare la somma dei primi 5 termini di una progressione geometrica il cui primo termine è uguale a 2 e la ragione uguale a 3.
Essendo a1=2, q=3, applicando la formula (8), si ha:

2)-Una progressione geometrica di ragione 2 è formata da tre termini la cui somma è 63. Trovare i termini della progressione.
Essendo q=2, S3=63, applicando la formula (8), si ha:

Da tal formula si ricava a1=9, quindi i termini della progressione sono 9, 18, 36.
3)-In una progressione geometrica la somma di tre numeri positivi è uguale a 52 e la differenza tra il secondo ed il primo numero è uguale ad 8. Trovare i tre numeri.
Indicando con x il secondo numero e con y la ragione, i tre numeri incogniti sono rappresentati da x/y, x, xy e, tenendo conto dei dati del problema, si può scrivere il sistema:

ossia, eliminando i denominatori (1)

Dividendo membro a membro le due equazioni, si ottiene l'equazione:

la cui forma intera è:
2y2 -11y+15=0
e ammette le radici y1=3, y2=5/2.
Sostituendo i valori trovati al posto della y, nella seconda equazione del sistema (1) si ricava, rispettivamente, x1=12, x2=40/3. I tre numeri cercati, sono:
4, 12, 36,
Tipi di medie
Media aritmetica
Definizione - Dicesi media aritmetica di n numeri la loro somma divisa per n.
Se si indicano con:
a1 + a2 + ... +an,
gli n numeri e con ma la loro media arirtmetica, per definizione, si ha:
La media aritmetica dei quattro numeri 5, -8, 7, 11, è data da:
Media ponderata
Se si indicano ora con:
r numeri interi positivi e si suppone di avere p1 numeri uguali al numero a1, p2 numeri uguali al numero a2, pr numeri uguali al numero a. La media aritmetica di tutti questi numeri, in base alla definizione data è uguale a:

che si può anche scrivere sotto la forma
Il valore di tale rapporto si chiama media ponderata dei numeri a1, a2 , ..., ar ed i numeri interi positivi p1, p2, ..., pr si chiamano rispettivamente pesi dei numeri a1, a2 ,..., ar.
Definizione - Si chiama media ponderata dei numeri a1, a2, ..., ar, di pesi rispettivamente p1, p2, ..., pr, la somma dei prodotti di questi numeri per i rispettivi pesi divisa per la somma dei pesi, cioè:
Esempio: trovare la media ponderata dei numeri 3/5, -4, 9, di pesi rispettivamente 15, 2, 3.
Si ha:

Media geometrica
Definizione - Si chiama media geometrica di n numeri positivi a1, a2, ..., an, la radice ennesima aritmetica del loro prodotto, cioè:

Esempio: trovare la media geometrica dei numeri 3, 18, 2, 12.
Si ha:

Media armonica

Esempio: trovare la media armonica dei numeri 2, 2/3, 3.
Si ha:

Nota bene
Se gli n numeri a1, a2, ..., an, sono tutti uguali fra loro e sono tutti positivi, allora la loro media aritmetica e la loro media armonica coincidono con il valore comune di uno qualsiasi di essi. Se invece i numeri a1, a2, ..., an, sono positivi e non tutti uguali, allora si può dimostrare che:
-la media aritmetica è maggiore della media geometrica e quest'ultima è maggiore di quella armonica.