MIKY & GENNY
SISTEMI DI EQUAZIONI DI PRIMO GRADO ---> INDICE
Nelle applicazioni pratiche
si possono considerare, oltre alle equazioni algebriche ad una sola
incognita, anche quelle a due o più incognite. In seguito
saranno trattate soltanto le equazioni algebriche a due sole incognite,
anche se le considerazioni fatte, valgono in generale.
Se con A(x, y) e B(x, y) si indicano due equazioni algebriche, nelle variabili x e y, non identiche fra loro, un'equazione nelle incognite x e y si può sempre rappresentare simbolicamente con la scrittura: (1) A(x, y)=B(x, y).
Si chiama soluzione dell'equazione (1) ogni coppia ordinata di numeri che, sostituiti rispettivamente ad x e y, fanno assumere alle due espressioni A(x, y) e B(x, y) valori uguali. Si osserva che: nella coppia ordinata dev'essere fissato il numero che si deve mettere al posto della x e quello al posto della y.
Per l'equazione (1) valgono le stesse definizioni date per le equazioni ad una sola incognita, e precisamente:
un'equazione a due incognite x e y, si dice intera quando i suoi due membri, A(x, y) e B(x, y), sono espressioni algebriche intere rispetto ad x e y, cioè quando sono due polinomi nelle variabili x e y. Se invece in A(x, y) e B(x, y), o in entrambi, vi sono frazioni che contengono almeno un'incognita al denominatore, l'equazione si dice fratta. L'equazione (1) si dice numerica quando, all'infuori delle incognite x e y, contiene soltanto numeri. Si dice invece letterale quando, all'infuori delle incognite x e y, contiene altre lettere che rappresentano numeri ben determinati.
Esempi:
1)-le equazioni nelle incognite x e y:

sono intere, la prima numerica, la seconda letterale.
2)-le equazioni nelle incognite x e y:
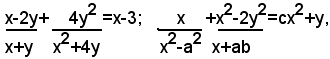
sono fratte, la prima numerica, la seconda letterale.
Inoltre, anche per le equazioni a due incognite valgono i principi di addizione, di trasporto e di moltiplicazione, dimostrati per le equazioni ad una sola incognita.
In base a tali principi, ogni equazione algebrica intera in due incognite x e y, e a coefficienti numerici, si potrà sempre scrivere sotto la forma: (2) A(x, y)=0, dove A(x, y) è un polinomio nelle variabili x e y, scritto sotto forma normale.
Il grado del polinomio A(x, y) si chiama grado dell'equazione. Quindi:
per trovare il grado di un'equazione intera a due incognite e a coefficienti numerici, bisogna prima scriverla sotto forma normale; il suo grado è il grado del polinomio che costituisce il primo membro.
Esempi:
1)-l'equazione, nelle incognite x, y: (2x+3y)2-3x2+5+7y2=(2+4y)2+x2+12xy+9x, scritta sotto forma normale, diventa: 9x+40y+20=0; essendo il suo primo membro un polinomio di primo grado, l'equazione data è di primo grado.
2)-l'equazione, nelle incognite x, y:

scritta sotto forma normale, diventa: x2y-3x2+9y2+x-3=0; essendo il suo primo membro un polinomio di terzo grado, l'equazione data è di terzo grado.
Nota bene
In seguito saranno considerate soltanto equazioni di primo grado.
Una tale equazione, ridotta a forma normale, può assumere la forma ax+by=c, dove a, b, c, indicano tre numeri assegnati.
Si vede facilmente che: un'equazione di primo grado a due incognite ammette sempre infinite soluzioni, cioè esistono sempre infinite coppie di numeri che, sostituiti rispettivamente alle incognite x e y, soddisfano l'equazione.
Ad esempio, si considera l'equazione (1) 5x+2y=8. Se alla x si attribuisce il valore 0, sostituendo nell'equazione (1) al posto della x il numero 0, si ottiene la seguente equazione di primo grado nell'incognita y: 2y=8, che ha per soluzione y=4. Quindi la soluzione dell'equazione (1) è data da x=0, y=4. Se invece alla x si attribuisce il valore 1, si ha per y l'equazione: 5+2y=8, che ha per soluzione y=3/2. Quindi x=1, y=3/2 è un'altra soluzione dell'equazione (1).
Insomma, ogni qualvolta si fissa ad arbitrio un numero, da attribuire all'incognita x, dalla (1) si ricava, in corrispondenza, un valore per la y; tale valore, assieme al valore fissato per la x, forma una coppia di numeri che costituisce una soluzione dell'equazione considerata.
Da tale ragionamento, segue che:
un'equazione di primo grado a due incognite ammette infinite soluzioni.
Sistemi di equazioni in due incognite
Considerate le due equazioni di primo grado: 3x-2y=8, 5x+3y=7, si sa che ognuna di esse ammette infinite soluzioni. Ci si chiede ora se le due equazioni ammettono soluzioni comuni, cioè se esistono delle coppie di numeri che, sostituiti rispettivamente ad x e y nelle due equazioni, le soddisfano entrambe. Quando si vuole risolvere un problema di questo tipo, si suol dire che si fa un sistema di equazioni; per indicare ciò, si scrivono di solito le equazioni una sotto l'altra, unendole con una parentesi graffa.
Per indicare che si vogliono trovare le soluzioni comuni alle due equazioni sopra considerate, si scrive:

In generale, un sistema di equazioni intere, a coefficienti numerici e a due incognite x e y, si può scrivere sotto la forma:

Siccome A(x, y) e B(x, y) sono polinomi nelle variabili x e y, scritti sotto forma normale, il sistema si dice scritto sotto forma normale.
Si chiama soluzione di un sistema di due equazioni in due incognite x e y, una coppia ordinata di numeri che, sostituiti rispettivamente ad x e y, soddisfano simultaneamente entrambe le equazioni. Risolvere un sistema di due equazioni in due incognite, vuol dire trovare tutte le soluzioni del sistema.
Un sistema di due equazioni in due incognite si dice determinato, indeterminato o impossibile, a seconda che ammette rispettivamente un numero finito di soluzioni, infinite soluzioni, nessuna soluzione.
Si chiama grado di un sistema, scritto sotto forma normale, il prodotto dei gradi delle delle singole equazioni.
Esempi:
1)-il sistema:

è di quindicesimo grado perchè, essendo la prima equazione di terzo grado e la seconda di quinto grado, risulta 3X5=15.
1)-il sistema:

è di secondo grado perchè, essendo la prima equazione di primo grado e la seconda di secondo grado, risulta 1X2=2.
Evidentemente, due sistemi equivalenti ad un terzo sistema, sono fra loro equivalenti ed inoltre se in un sistema di due equazioni in due incognite, si sostituiscono le due equazioni con altre due ad esse rispettivamente equivalenti, si ottiene un sistema equivalente a quello assegnato.
Teorema - il sistema (1)

di due equazioni algebriche a due incognite x e y, è equivalente al sistema: (2)
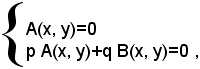
dove p e q sono due numeri qualsiasi, con q≠0.
Si deve osservare che la seconda equazione del sistema (2) si è ottenuta dal sistema (1) moltiplicando ambo i membri della prima equazione per il numero p, ambo i membri della della seconda equazione per il numero q e poi sommando membro a membro le due equazioni così ottenute.
Dimostrazione: per definizione di sistemi equivalenti, si deve dimostrare che ogni soluzione del sistema (1) è anche soluzione del sistema (2) e, viceversa, che ogni soluzione del sistema (2) è anche soluzione del sistema (1). Si dimostra la prima parte e si suppone che i numeri x=α, y=β, costituiscono una soluzione del sistema (1). Ciò significa che se si calcolano le due espressioni A(x, y) e B(x, y) per x=α, y=β, esse assumono il valore zero. Per l'ipotesi fatta, si ha:

Ma se A(α, β) e B(α, β) valgono zero, anche il valore dell'espressione p.A(α, β)+q.B(α, β), qualunque siano i valori di p e q, quindi si ha:

e ciò prova che x=α, y=β è anche una soluzione del sistema (2). Si dimostra ora la seconda parte, cioè si suppone che i numeri x=γ, y=δ, sia una souzione del sistema (2), cioè sia (3)

e si prova che x=γ, y=δ una souzione del sistema (1).Infatti, siccome A(γ, δ) vale per ipotesi zero, la (3) si può scrivere come segue:
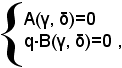
ed essendo per ipotesi q≠0, risulta:

e ciò prova che x=γ, y=δ è anche una souzione del sistema (1). Resta così dimostrato completamente il teorema.
Sistemi di equazioni di primo grado in due incognite
Ogni sistema di equazioni di primo grado in due incognite x, y, a coefficienti numerici, ridotto a forma normale, si può scrivere sotto la forma seguente: (1)
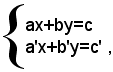
dove a, b, c, a', b', c' indicano numeri noti. I numeri a, b, a', b' si chiamano coefficienti delle incognite, mentre c, c' si chiamano termini noti.
Si vuole ora trovare una regola che permetta di decidere se il sistema (1) ammette o no soluzioni e, nel caso affermativo, quante ne ammette. Si suppone prima che nel sistema (1) sia nullo uno dei coefficienti delle incognite, cioè, ad esempio, che sia b=0, a≠0, a'≠0, b'≠0. In questa ipotesi il sistema (1) si può scrivere sotto la forma: (2)

e si dimostra che questo sistema (1) ammette una ed una sola soluzione.
Infatti, essendo la prima equazione del sistema (2) un'equazione di primo grado nell'incognita x, essa, come è noto, ammette una ed una sola soluzione data da:

Sostituendo ora questo valore al posto della x, nella seconda equazione del sistema (2), si ottiene l'equazione:

che è un'equazione di primo grado nell'incognita y; essa perciò ammette una sola soluzione data da:

Dal ragionamento svolto, segue che il sistema (2) è soddisfatto soltanto dalla coppia di numeri:

cioè esso ammette una ed una sola soluzione.
Si può quindi dire che: quando in un sistema di due equazioni di primo grado in due incognite, è nullo uno dei coefficienti delle incognite e gli altri sono diversi da zero, allora il sistema ammette una ed una sola soluzione.
Alla stessa conclusione si arriva se b=0, a'=0 a≠0, b'≠0.
Esempio: risolvere il sistema:

La prima equazione del sistema è soddisfatta per y=3; sostituendo questo valore al posto della y nella seconda equazione, si ottiene un'equazione nella sola incognita x: 3x+15=9, dalla quale si ricava x=-2. Perciò il sistema dato ammette la soluzione x=-2, y=3 e soltanto questa.
Si suppone ora che i coefficienti delle incognite del sistema: (1)
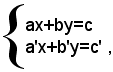
siano tutti diversi da zero, cioè sia: a≠0, b≠0, a'≠0, b'≠0.
Per decidere in questo caso se il sistema ammette soluzioni o no, e in caso affermativo quante ne ammette, si distinguono tre casi, a seconda che, nel sistema (1), i coefficienti delle incognite di ugual nome non sono fra loro proporzionali, oppure sono fra loro proporzionali senza esserlo i termini noti, oppure i coefficienti delle incognite ed i termini noti delle due equazioni sono fra loro proporzionali.
Si ricorda che 4 numeri a, a', b, b', considerati nell'ordine scritto, si dicono fra loro proporzionali, quando risulta a/a'=b/b'.
Pertanto, si devono considerare i seguenti casi:

che saranno esaminati singolarmente.
1° Caso - Si suppone che i coefficienti delle incognite del sistema (1) non sono fra loro proporzionali, cioè: (2)
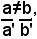
si dimostra che, in tali ipotesi, il sistema (1) ammette una ed una sola soluzione.
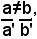
cioè nell'ipotesi che i coefficienti delle incognite di egual nome delle due equazioni, non siano fra loro proporzionali. In tal caso si è visto che l'unica soluzione del sistema è data da: (8)

Per ricordare a memoria le formule (8), si introduce il simbolo di matrice. Se α, β, γ, δ, sono 4 numeri qualsiasi, si chiama matrice quadrata del 2° ordine il seguente simbolo: (1)

Si chiama determinante del 2° ordine, rappresentato dalla matrice (1) e si indica con il simbolo:
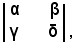
il numero: αδ-βγ, cioè si pone per definizione:

Esempi:
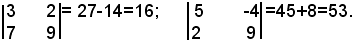
Pertanto, si ha anche la regola pratica per determinare effettivamente questa soluzione.
Premesso ciò, si vede che le formule (8) si possono scrivere sotto la forma seguente:

Esempi:
1)-risolvere il sistema:

In questo caso risulta: (9) a=3, b=-2, c=-7, a'=2, b'=7, c'=37, ed i coefficienti delle incognite non sono proporzionali. Il sistema ammette allora una sola soluzione, che si ricava dalle formule (8) sostituendo in esse, alle lettere, i valori (9). Effettuando questa sostituzione si trova:
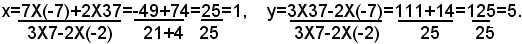
La soluzione del sistema è quindi: x=1, y=5.
Con l'uso dei determinanti si ha:

2)-il sistema:

è impossibile, perchè i coefficienti delle incognite non sono proporzionali fra loro e non ai termini noti.

è indeterminato, perchè i coefficienti delle incognite e i termini noti sono tutti proporzionali fra loro.Per evitare di imparare a memoria le formule (8), si usano alcuni metodi di risoluzione del sistema (1).
1° - Metodo di riduzione o addizione
Dato il sistema: (1)
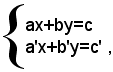
e supposto
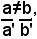
si moltiplicano ambo i membri della prima equazione per il numero b' ed ambo i membri della seconda equazione per il numero -b e sommando membro a membro le due equazioni, si ottiene l'equazione: (ab'-a'b)x=b'c-bc'. In modo del tutto analogo, moltiplicando ambo i membri della prima equazione per il numero -a' ed ambo i membri della seconda equazione per il numero a e poi sommando membro a membro le due equazioni, si ottiene l'equazione: (ab'-a'b)y=ac'-a'c. Si ha così il sistema: (2)

che ammette, essendo ab'-a'b≠0, l'unica soluzione:

Siccome la soluzione ottenuta, come è noto, è anche del sistema (1), risolvere il sistema (1),equivale
a risolvere il sistema (2) ad esso equivalente. In pratica, per
ottenere la prima equazione del sistema (2), basta moltiplicare ambo i
membri di ciascuna equazione del sistema 1) per un numero diverso da
zero, in modo che i coefficienti della y risultino numeri opposti e poi
sommare membro a membro le due equazioni. Per ottenere la seconda
equazione, devono essere opposti i coeficienti della x .
Esempi:
1)-Risolvere il sistema:

In questo sistema i coefficienti delle incognite non sono proporzionali e perciò esso ammette una ed una sola soluzione.
Per eliminare la y, siccome il m. c. m. dei coefficienti della y è 12, basta moltiplicare ambo i membri della prima equazione per 3 e ambo i membri della seconda equazione per 2 e poi sommare membro a membro le due equazioni, si ha: 9x+12y+10x-12y=54-16, ossia 19x=38, da cui x=2. Moltiplicando ora ambo i membri della prima equazione per 5 e ambo i membri della seconda equazione per -3 e poi sommando membro a membro le due equazioni, si ha: 15x+20y-15x+18y=90+24, ossia 38y=114, da cui y=3. La soluzione del sistema è quindi: x=2, y=3.2)-Risolvere il sistema:
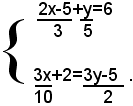
Si riduce il sistema a forma normale, liberando le equazioni dai denominatori, trasportando poi i termini contenenti le incognite nel primo membro e i termini noti nel secondo ed infine riducendo i termini simili, si ha:

ossia:

In questo sistema i coefficienti delle incognite non sono proporzionali e perciò esso ammette una ed una sola soluzione. Per eliminare la y, siccome il m. c. m. dei coefficienti della y è 15, basta moltiplicare ambo i membri della prima equazione per 5 e ambo i membri della seconda equazione per 3 e poi sommare membro a membro le due equazioni, si ha: 50x+15y+3x-15y=575-45, ossia: 53x=530, da cui: x=10. Per eliminare la x, basta moltiplicare ambo i membri della seconda equazione per -10 e poi sommare membro a membro le due equazioni, si ha: 10x+3y-10x+50y=115+150, ossia: 53y=265, da cui: y=5. La soluzione del sistema è quindi: x=10, y=5.
Dal metodo di addizione si può dedurre la seguente regola:
-per risolvere col metodo di addizione un sistema di due equazioni di primo grado in due incognite, ridotto a forma normale, si moltiplicano ambo i membri delle due equazioni per numeri diversi da zero, tali che i coefficienti di una delle incognite, per esempio y, risultino opposti. Dopo di ciò, sommando membro a membro le due equazioni, si ottiene un'equazione nella sola incognita x, che risolta, dà il valore della x. Con lo stesso procedimento si ricava il valore dell'incognita y.
Metodo di sostituzione
Dato il sistema: (1)
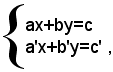
e supposto
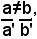
si risolve, ad esempio la prima equazione rispetto alla lettera y, e nell'altra equazione si sostituisce a tale incognita l'espressione trovata; si ottiene il sistema: (2)

In tale sistema, la seconda equazione contiene la sola incognita y e, risolvendola si ottiene il valore della x, che sostituito nella prima equazione, dopo facili calcoli, ci fornisce il valore della y e che il sistema (2) ammette la soluzione:

Questa è anche la soluzione del sistema (1), come è noto.
ossia:

o anche:

cioè:

Sostituendo, nella prima equazione, ad x il valore trovato, si ha:
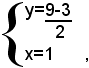
ossia:

La soluzione del sistema è quindi: x=1, y=3.
2)-risolvere il sistema:

Si riduce il sistema sotto forma normale, liberando le equazioni dai denominatori, trasportando nel primo membro i termini contenenti le incognite e i termini noti nel secondo e riducendo i termini simili, si ottiene:

cioè un sistema in cui i coefficienti delle incognite non sono proporzionali. Ricavando la y dalla prima equazione e sostituendo l'espressione trovata al posto della y nella seconda equazione, si ha:

da cui, risolvendo la seconda equazione, si ha:

e quindi:

La soluzione del sistema è quindi: x=4, y=10.
Metodo del confronto
Per risolvere col metodo del confronto un sistema di due equazioni di primo grado in due incognite, ridotto a forma normale, bisogna innanzitutto osservare che questo è un caso particolare del metodo di sostituzione. Precisamente, mentre con il metodo di sostituzione si risolveva una sola delle due equazioni rispetto ad un'incognita, ora si risolvono le due equazioni rispetto alla stessa incognita.
Esempio: risolvere il sistema:

nel quale i coefficienti delle incognite non sono proporzionali. Risolvendo entrambe le equazioni rispetto alla y, si ottiene il seguente sistema:

che è equivalente a quello assegnato. Sostituendo, nella seconda equazione, al posto della y, l'espressione data dalla prima equazione, si ha il sistema equivalente seguente:

nel quale la seconda equazione contiene la sola incognita x. Risolvendo la seconda equazione, si trova il sistema:

da cui, sostituendo nella prima equazione il valore trovato della x, risulta:
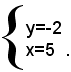
La soluzione del sistema è quindi: x=5, y=-2.
Nota bene
I procedimenti indicati per risolvere i sistemi di due equazioni di primo grado in due incognite, con i coefficienti numerici, si prestano anche per risolvere i sistemi interi di primo grado a coefficienti letterali, oppure i sistemi fratti che, ridotti a forma normale, danno luogo ad un sistema di primo grado. Nel primo caso, cioè quando i coefficienti sono letterali, bisogna escludere, per le lettere, quegli eventuali particolari valori che fanno perdere di significato ad almeno una delle due equazioni del sistema. Si dovrà poi anche vedere se esistono dei particolari valori delle lettere per i quali il sistema diventa impossibile o indeterminato. Nel secondo caso invece, poichè per trasformare il sistema fratto a forma normale, si devono moltiplicare ambo i membri delle equazioni per un'espressione contenente almeno un'incognita, potrebbe capitare che il sistema così ottenuto avesse più soluzioni di quello assegnato, analogamente a quanto visto per le equazioni fratte. Perciò, dopo aver risolto questo secondo sistema, occorrerà sempre appurare se le soluzioni trovate soddisfano, oppure no, anche il sistema assegnato. Per far ciò, basterà solamente verificare se i valori trovati annullano o no i denominatori che compaiono nel sistema dato, come già si è visto nel caso di una sola equazione.
Esempi:
1)-risolvere il sistema:
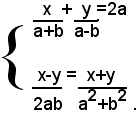
Si liberano dapprima le equazioni dai denominatori, perciò si devono moltiplicare ambo i membri della prima equazione per (a+b)(a-b) ed ambo i membri della seconda per 2ab(a2+b2), dopo aver supposto (1) a≠-b, a≠b, a≠0, b≠0. Dopo facili calcoli, si ha: (2)

Bisogna osservare che, nelle ipotesi (1) i coefficienti delle variabili del sistema (2), non sono fra loro proporzionali, perciò il sistema ammette una ed una sola soluzione. Si risolve ora il sistema con il metodo di addizione e, a tale scopo, si moltiplicano ambo i membri della prima equazione per (a+b) e si sommano membro a membro le due equazioni, si ottiene:
(a-b)(a+b)x+(a-b)2x=2a(a2-b2)(a+b), ossia, dividendo ambo i membri per a-b, che è un numero diverso da zero, si ha: (a+b)x+(a-b)x=2a(a+b)(a-b), cioè: 2ax=2a(a+b)2; da cui, essendo a≠0, si ha: x=(a+b)2. Se invece si moltiplicano ambo i membri della prima equazione del sistema (2) per -(a-b) e poi si sommano membro a membro le due equazioni del sistema, si ha: y=(a-b)2. Pertanto, nelle ipotesi (1), il sistema dato ammette una ed una sola soluzione data da x=(a+b)2, y=(a-b)2.
2)-risolvere il sistema:
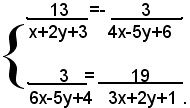
Questo è un sistema fratto; liberando le equazioni dai denominatori, si ottiene il sistema:

ossia, dopo facili semplificazioni:
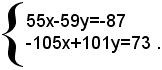
Risolvendo il sistema con uno qualsiasi dei metodi trattati, si ottiene: x=7, y=8, che è anche una soluzione del sistema (1), dato che per tali valori, non si annulla nessun denominatore del sistema dato.
3)-risolvere il sistema:

Liberando le equazioni dai denominatori, dopo facili calcoli, si ottiene:

Risolvendo il sistema, si trova x=2, y=3. Questa soluzione non soddisfa però il sistema dato, perchè, per x=2, si annulla il denominatore della prima equazione. Perciò, il sistema considerato è impossibile.
Risoluzione dei sistemi di tre o più equazioni di primo grado con altrettante incognite
I metodi di risoluzione, trattati per i sistemi di due equazioni di primo grado in due incognite, si possono applicare anche ai sistemi di tre o più equazioni di primo grado con altrettante incognite. Si vede ora come si deve procedere su un esempio.
Risolvere il seguente sistema, scritto sotto forma normale: (1)

Risoluzione con il metodo di sostituzione
Si ricava, ad esempio, il valore della x dalla prima equazione e lo si sostituisce, al posto della x nelle altre due equazioni, ottenendo così il sistema:

ossia, dopo facili semplificazioni:

Risolvendo il sistema formato dalle ultime due equazioni, nelle incognite y e z, si ha:

Sostituendo ora, nella prima equazione, ad y e z i valori trovati, si ha:
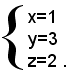
L'unica soluzione del sistema è quindi: x=1, y=3, z=2.
Risoluzione con il metodo di confronto
Risolvendo le tre equazioni del sistema (1) rispetto, ad esempio, alla x, si ottiene il sistema:
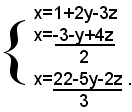
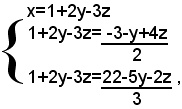
nel quale le ultime due equazioni contengono le due sole incognite y e z. Risolvendo il sistema formato da queste due ultime equazioni, con facili calcoli si trova:

Evidentemente, si ha:
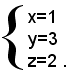
Tale soluzione è la stessa di quella trovata con il metodo di sostituzione.
Risoluzione con il metodo di addizione
Fra le prime due equazioni del sistema (1), si elimina, ad esempio, la x, moltiplicando ambo i membri della prima equazione per -2 e poi sommando membro a membro le due equazioni, si ottiene: -2x+4y-6z+2x+y-4z=-2-3, ossia: y-2z=-1. Si elimina ora la x tra la prima e la terza equazione, moltiplicando ambo i membri della prima equazione per -3 e poi sommando membro a membro le due equazioni. Con facili calcoli si trova: 11y-7z=19. Risolvendo ora, con un metodo qualsiasi, il sistema:

si trova y=3, z=2. Sostituendo questi valori, al posto, rispettivamente di y e z, in una qualsiasi delle equazioni del sistema (1), si trova x=1. Perciò, x=1, y=3, z=2 è l'unica soluzione del sistema dato.
Problemi di primo grado a più incognite
Si considerano ora alcuni problemi che si traducono in due o più equazioni di primo grado con altrettante incognite.
1)-Si trovi la frazione che diventa uguale a 1/3, quando si aggiunge 1 al numeratore, ed uguale a 1/4, quando invece si aumenta di 1 il denominatore.
Si indica con x il numeratore della frazione cercata e con y il denominatore. I numeri x e y devono essere quindi numeri interi. La prima condizione data dal problema si traduce nella seguente equazione:

mentre la seconda condizione, si traduce nell'equazione:
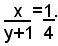
Il problema perciò si si traduce nel seguente sistema fratto: (1)

Liberando le equazioni del sistema dai denominatori, si ottiene:

e dopo facili calcoli risulta x=4, y=15, quindi la frazione cercata è 4/15.
2)-Si ha la somma di € 39500, costituita da banconote di € 500, € 1000, € 5000. Il doppio delle banconote da € 500 aumentato del numero delle banconote da € 1000, dà il numero delle banconote da € 5000, aumentato di 5. Il quintuplo delle banconote da € 5000, diminuito del triplo delle banconote da € 1000, dà il quadruplo delle banconote da € 500 aumentato di 9. Trovare il numero delle banconote di ciascuna specie.
Si indicano con x, y, z, rispettivamente i numeri dei biglietti da € 500, € 1000, € 5000. Poichè l'ammontare della somma è € 39500, deve risultare: 500x+1000y+5000z=€ 39500. Per la seconda condizione del problema, si ha: 2x+y=z+5, e per la terza condizione, risulta: 5z-3y=4x+9. Il problema si traduce quindi nel sistema:

e, dopo semplificazioni, diventa:
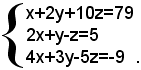
Si risolve ora il sistema con il metodo di sostituzione: si ricava il valore della y dalla seconda equazione, e lo si sostituisce, al posto della y, nelle altre due equazioni, si ottiene:

Risolvendo il sistema formato dalle due ultime equazioni nelle incognite x e z, con un metodo qualsiasi, si ha: x=5, z=7. Sostituendo questi valori al posto, rispettivamente della x e della y, nella prima equazione, si ricava y=2. Perciò la soluzione del sistema è x=5, y=2, z=7.Si conclude quindi che, le banconote da € 500, € 1000, € 5000 sono rispettivamente, in numero 5, 2, 7.
3)-Calcolare le misure dei lati di un rettangolo, sapendo che se si aumenta l'altezza di m 3 e si diminuisce di altrettanto la base, l'area del rettangolo non cambia. Invece se si aumenta l'altezza di m 5 e si diminuisce la base di m 3, la superficie del rettangolo aumenta di 16 m2. Si indica con x la misura dell'altezza e con y quella della base del rettangolo; l'area è data da xy. Se si aumenta l'altezza di m 3 e si diminuisce la base di altrettanto, l'area del nuovo rettangolo è (x+3)(y-3), perciò, per la prima condizione del problema, si può scrivere l'equazione: (x+3)(y-3)=xy. Analogamente, per la seconda condizione del problema, si può scrivere anche l'equazione: (x+5)(y-3)=xy+16. Il problema si traduce quindi nel seguente sistema:

e, dopo semplificazioni, diventa:

Risolvendo questo sistema, con un metodo qualsiasi, si trova che esso ammette la seguente soluzione: x=8, y=11. Perciò, la misura dell'altezza del rettangolo è 8, mentre quella della base è 11.
Se con A(x, y) e B(x, y) si indicano due equazioni algebriche, nelle variabili x e y, non identiche fra loro, un'equazione nelle incognite x e y si può sempre rappresentare simbolicamente con la scrittura: (1) A(x, y)=B(x, y).
Si chiama soluzione dell'equazione (1) ogni coppia ordinata di numeri che, sostituiti rispettivamente ad x e y, fanno assumere alle due espressioni A(x, y) e B(x, y) valori uguali. Si osserva che: nella coppia ordinata dev'essere fissato il numero che si deve mettere al posto della x e quello al posto della y.
Per l'equazione (1) valgono le stesse definizioni date per le equazioni ad una sola incognita, e precisamente:
un'equazione a due incognite x e y, si dice intera quando i suoi due membri, A(x, y) e B(x, y), sono espressioni algebriche intere rispetto ad x e y, cioè quando sono due polinomi nelle variabili x e y. Se invece in A(x, y) e B(x, y), o in entrambi, vi sono frazioni che contengono almeno un'incognita al denominatore, l'equazione si dice fratta. L'equazione (1) si dice numerica quando, all'infuori delle incognite x e y, contiene soltanto numeri. Si dice invece letterale quando, all'infuori delle incognite x e y, contiene altre lettere che rappresentano numeri ben determinati.
Esempi:
1)-le equazioni nelle incognite x e y:

sono intere, la prima numerica, la seconda letterale.
2)-le equazioni nelle incognite x e y:
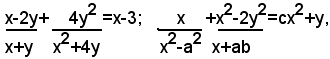
sono fratte, la prima numerica, la seconda letterale.
Inoltre, anche per le equazioni a due incognite valgono i principi di addizione, di trasporto e di moltiplicazione, dimostrati per le equazioni ad una sola incognita.
In base a tali principi, ogni equazione algebrica intera in due incognite x e y, e a coefficienti numerici, si potrà sempre scrivere sotto la forma: (2) A(x, y)=0, dove A(x, y) è un polinomio nelle variabili x e y, scritto sotto forma normale.
Il grado del polinomio A(x, y) si chiama grado dell'equazione. Quindi:
per trovare il grado di un'equazione intera a due incognite e a coefficienti numerici, bisogna prima scriverla sotto forma normale; il suo grado è il grado del polinomio che costituisce il primo membro.
Esempi:
1)-l'equazione, nelle incognite x, y: (2x+3y)2-3x2+5+7y2=(2+4y)2+x2+12xy+9x, scritta sotto forma normale, diventa: 9x+40y+20=0; essendo il suo primo membro un polinomio di primo grado, l'equazione data è di primo grado.
2)-l'equazione, nelle incognite x, y:

scritta sotto forma normale, diventa: x2y-3x2+9y2+x-3=0; essendo il suo primo membro un polinomio di terzo grado, l'equazione data è di terzo grado.
Nota bene
In seguito saranno considerate soltanto equazioni di primo grado.
Una tale equazione, ridotta a forma normale, può assumere la forma ax+by=c, dove a, b, c, indicano tre numeri assegnati.
Si vede facilmente che: un'equazione di primo grado a due incognite ammette sempre infinite soluzioni, cioè esistono sempre infinite coppie di numeri che, sostituiti rispettivamente alle incognite x e y, soddisfano l'equazione.
Ad esempio, si considera l'equazione (1) 5x+2y=8. Se alla x si attribuisce il valore 0, sostituendo nell'equazione (1) al posto della x il numero 0, si ottiene la seguente equazione di primo grado nell'incognita y: 2y=8, che ha per soluzione y=4. Quindi la soluzione dell'equazione (1) è data da x=0, y=4. Se invece alla x si attribuisce il valore 1, si ha per y l'equazione: 5+2y=8, che ha per soluzione y=3/2. Quindi x=1, y=3/2 è un'altra soluzione dell'equazione (1).
Insomma, ogni qualvolta si fissa ad arbitrio un numero, da attribuire all'incognita x, dalla (1) si ricava, in corrispondenza, un valore per la y; tale valore, assieme al valore fissato per la x, forma una coppia di numeri che costituisce una soluzione dell'equazione considerata.
Da tale ragionamento, segue che:
un'equazione di primo grado a due incognite ammette infinite soluzioni.
Sistemi di equazioni in due incognite
Considerate le due equazioni di primo grado: 3x-2y=8, 5x+3y=7, si sa che ognuna di esse ammette infinite soluzioni. Ci si chiede ora se le due equazioni ammettono soluzioni comuni, cioè se esistono delle coppie di numeri che, sostituiti rispettivamente ad x e y nelle due equazioni, le soddisfano entrambe. Quando si vuole risolvere un problema di questo tipo, si suol dire che si fa un sistema di equazioni; per indicare ciò, si scrivono di solito le equazioni una sotto l'altra, unendole con una parentesi graffa.
Per indicare che si vogliono trovare le soluzioni comuni alle due equazioni sopra considerate, si scrive:

In generale, un sistema di equazioni intere, a coefficienti numerici e a due incognite x e y, si può scrivere sotto la forma:

Siccome A(x, y) e B(x, y) sono polinomi nelle variabili x e y, scritti sotto forma normale, il sistema si dice scritto sotto forma normale.
Si chiama soluzione di un sistema di due equazioni in due incognite x e y, una coppia ordinata di numeri che, sostituiti rispettivamente ad x e y, soddisfano simultaneamente entrambe le equazioni. Risolvere un sistema di due equazioni in due incognite, vuol dire trovare tutte le soluzioni del sistema.
Un sistema di due equazioni in due incognite si dice determinato, indeterminato o impossibile, a seconda che ammette rispettivamente un numero finito di soluzioni, infinite soluzioni, nessuna soluzione.
Si chiama grado di un sistema, scritto sotto forma normale, il prodotto dei gradi delle delle singole equazioni.
Esempi:
1)-il sistema:

è di quindicesimo grado perchè, essendo la prima equazione di terzo grado e la seconda di quinto grado, risulta 3X5=15.
1)-il sistema:

è di secondo grado perchè, essendo la prima equazione di primo grado e la seconda di secondo grado, risulta 1X2=2.
Evidentemente, due sistemi equivalenti ad un terzo sistema, sono fra loro equivalenti ed inoltre se in un sistema di due equazioni in due incognite, si sostituiscono le due equazioni con altre due ad esse rispettivamente equivalenti, si ottiene un sistema equivalente a quello assegnato.
Teorema - il sistema (1)

di due equazioni algebriche a due incognite x e y, è equivalente al sistema: (2)
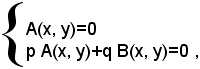
dove p e q sono due numeri qualsiasi, con q≠0.
Si deve osservare che la seconda equazione del sistema (2) si è ottenuta dal sistema (1) moltiplicando ambo i membri della prima equazione per il numero p, ambo i membri della della seconda equazione per il numero q e poi sommando membro a membro le due equazioni così ottenute.
Dimostrazione: per definizione di sistemi equivalenti, si deve dimostrare che ogni soluzione del sistema (1) è anche soluzione del sistema (2) e, viceversa, che ogni soluzione del sistema (2) è anche soluzione del sistema (1). Si dimostra la prima parte e si suppone che i numeri x=α, y=β, costituiscono una soluzione del sistema (1). Ciò significa che se si calcolano le due espressioni A(x, y) e B(x, y) per x=α, y=β, esse assumono il valore zero. Per l'ipotesi fatta, si ha:

Ma se A(α, β) e B(α, β) valgono zero, anche il valore dell'espressione p.A(α, β)+q.B(α, β), qualunque siano i valori di p e q, quindi si ha:

e ciò prova che x=α, y=β è anche una soluzione del sistema (2). Si dimostra ora la seconda parte, cioè si suppone che i numeri x=γ, y=δ, sia una souzione del sistema (2), cioè sia (3)

e si prova che x=γ, y=δ una souzione del sistema (1).
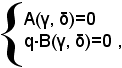
ed essendo per ipotesi q≠0, risulta:

e ciò prova che x=γ, y=δ è anche una souzione del sistema (1). Resta così dimostrato completamente il teorema.
Sistemi di equazioni di primo grado in due incognite
Ogni sistema di equazioni di primo grado in due incognite x, y, a coefficienti numerici, ridotto a forma normale, si può scrivere sotto la forma seguente: (1)
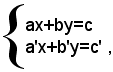
dove a, b, c, a', b', c' indicano numeri noti. I numeri a, b, a', b' si chiamano coefficienti delle incognite, mentre c, c' si chiamano termini noti.
Si vuole ora trovare una regola che permetta di decidere se il sistema (1) ammette o no soluzioni e, nel caso affermativo, quante ne ammette. Si suppone prima che nel sistema (1) sia nullo uno dei coefficienti delle incognite, cioè, ad esempio, che sia b=0, a≠0, a'≠0, b'≠0. In questa ipotesi il sistema (1) si può scrivere sotto la forma: (2)

e si dimostra che questo sistema (1) ammette una ed una sola soluzione.
Infatti, essendo la prima equazione del sistema (2) un'equazione di primo grado nell'incognita x, essa, come è noto, ammette una ed una sola soluzione data da:
Sostituendo ora questo valore al posto della x, nella seconda equazione del sistema (2), si ottiene l'equazione:
che è un'equazione di primo grado nell'incognita y; essa perciò ammette una sola soluzione data da:
Dal ragionamento svolto, segue che il sistema (2) è soddisfatto soltanto dalla coppia di numeri:

cioè esso ammette una ed una sola soluzione.
Si può quindi dire che: quando in un sistema di due equazioni di primo grado in due incognite, è nullo uno dei coefficienti delle incognite e gli altri sono diversi da zero, allora il sistema ammette una ed una sola soluzione.
Alla stessa conclusione si arriva se b=0, a'=0 a≠0, b'≠0.
Esempio: risolvere il sistema:

La prima equazione del sistema è soddisfatta per y=3; sostituendo questo valore al posto della y nella seconda equazione, si ottiene un'equazione nella sola incognita x: 3x+15=9, dalla quale si ricava x=-2. Perciò il sistema dato ammette la soluzione x=-2, y=3 e soltanto questa.
Si suppone ora che i coefficienti delle incognite del sistema: (1)
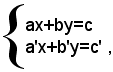
siano tutti diversi da zero, cioè sia: a≠0, b≠0, a'≠0, b'≠0.
Per decidere in questo caso se il sistema ammette soluzioni o no, e in caso affermativo quante ne ammette, si distinguono tre casi, a seconda che, nel sistema (1), i coefficienti delle incognite di ugual nome non sono fra loro proporzionali, oppure sono fra loro proporzionali senza esserlo i termini noti, oppure i coefficienti delle incognite ed i termini noti delle due equazioni sono fra loro proporzionali.
Si ricorda che 4 numeri a, a', b, b', considerati nell'ordine scritto, si dicono fra loro proporzionali, quando risulta a/a'=b/b'.
Pertanto, si devono considerare i seguenti casi:
che saranno esaminati singolarmente.
1° Caso - Si suppone che i coefficienti delle incognite del sistema (1) non sono fra loro proporzionali, cioè: (2)
si dimostra che, in tali ipotesi, il sistema (1) ammette una ed una sola soluzione.
Tenendo conto che il sistema (1) si può scrivere anche sotto la forma: (1')

e che per il teorema precedente è equivalente al sistema: (3)

la cui seconda equazione è ottenuta dal sistema (1') moltiplicando ambo i membri della prima equazione per il numero b', ambo i membri della seconda equazione per il numero -b e poi sommando membro a membro, le due equazioni così ottenute. Il sistema (3), dopo facili semplificazioni, si può scrivere sotto la forma seguente: (4)
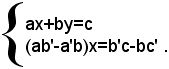
Si può quindi dire che risolvere il sistema (1) o il sistema (4) è perfettamente la stessa cosa, siccome i due sistemi sono equivalenti. Premesso cio, bisogna osservare che, nella seconda equazione del sistema (4), il coefficiente della y è zero, mentre il coefficiente della x, è diverso da zero. Infatti, dall'ipotesi (2) a/a'≠b/b', moltiplicando sia il numero a/a' che il numero b/b' per il numero non nullo a'b', si ottiene a'b'a/a'=a'b'b/b, ossia ab'≠a'b, o anche ab'-a'b≠0.
In base a quanto dimostrato in precedenza, si può affermare che il sistema (4), e quindi anche il sistema (1), ammette una ed una sola soluzione. Ricavando il valore della x dalla seconda equazione, si ottiene:

Sostituendo questo valore, al posto della x, nella seconda equazione, si ha:
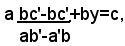
da cui, dopo facili calcoli, si ricava:

Si può quindi dire che: quando nel sistema (1) i coefficienti delle incognite sono diversi da zero e non sono fra loro proporzionali, il sistema ammette una ed una sola soluzione data da:

2° Caso - Si suppone che i coefficienti delle incognite del sistema (1) sono fra loro proporzionali senza esserlo i termini noti, cioè: (5)

Si deve osservare che da a/a'=b/b', segue che ab'-a'b=0, e da b/b'≠c/c', segue che b'c-bc'≠0.
Ciò premesso, nelle ipotesi (5), il sistema (4) si può scrivere sotto la seguente forma:

e si vede facilmente che questo sistema, e quindi anche il sistema (1), è impossibile, cioè non ammette nessuna soluzione. Basta infatti osservare che la seconda equazione del sistema non può essere soddisfatta da nessun valore della x, essendo per ipotesi b'c-bc'≠0. Si può quindi dire che: se nel sistema (1) sono proporzionali solo i coefficienti delle incognite, il sistema è impossibile.
3° Caso - Si suppone che nel sistema (1) i coefficienti delle incognite e i termini noti delle due equazioni sono fra loro proporzionali, cioè: (6)
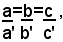
si dimostra in tale ipotesi che il sistema è indeterminato.
Dalla (6) si ricava ab'-a'b=0, bc'-b'c=0, perciò il sistema (4) diventa: (7)

Siccome la seconda uguaglianza delle (7) è un'identità, cioè è soddisfatta da qualsiasi valore attribuito alla x, il sistema (7), e quindi anche il sistema (1), ammette come soluzioni tutte e solo le soluzioni della prima equazione del sistema che, come è noto, sono infinite. Il sistema, ammettendo infinite soluzioni, è indeterminato.
Si può quindi dire che: se nel sistema (1) i coefficienti delle incognite ed i termini noti delle due equazioni sono fra loro proporzionali, comprendendo nella proporzionalità anche il caso in cui i due termini noti siano nulli, il sistema è indeterminato e le sue soluzioni sono tutte e sole le soluzioni di una qualsiasi delle due equazioni.
Dalla discussione fatta, segue che il sistema (1), si deve risolvere solo nell'ipotesi che sia
e che per il teorema precedente è equivalente al sistema: (3)

la cui seconda equazione è ottenuta dal sistema (1') moltiplicando ambo i membri della prima equazione per il numero b', ambo i membri della seconda equazione per il numero -b e poi sommando membro a membro, le due equazioni così ottenute. Il sistema (3), dopo facili semplificazioni, si può scrivere sotto la forma seguente: (4)
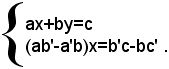
Si può quindi dire che risolvere il sistema (1) o il sistema (4) è perfettamente la stessa cosa, siccome i due sistemi sono equivalenti. Premesso cio, bisogna osservare che, nella seconda equazione del sistema (4), il coefficiente della y è zero, mentre il coefficiente della x, è diverso da zero. Infatti, dall'ipotesi (2) a/a'≠b/b', moltiplicando sia il numero a/a' che il numero b/b' per il numero non nullo a'b', si ottiene a'b'a/a'=a'b'b/b, ossia ab'≠a'b, o anche ab'-a'b≠0.
In base a quanto dimostrato in precedenza, si può affermare che il sistema (4), e quindi anche il sistema (1), ammette una ed una sola soluzione. Ricavando il valore della x dalla seconda equazione, si ottiene:
Sostituendo questo valore, al posto della x, nella seconda equazione, si ha:
da cui, dopo facili calcoli, si ricava:
Si può quindi dire che: quando nel sistema (1) i coefficienti delle incognite sono diversi da zero e non sono fra loro proporzionali, il sistema ammette una ed una sola soluzione data da:
2° Caso - Si suppone che i coefficienti delle incognite del sistema (1) sono fra loro proporzionali senza esserlo i termini noti, cioè: (5)
Si deve osservare che da a/a'=b/b', segue che ab'-a'b=0, e da b/b'≠c/c', segue che b'c-bc'≠0.
Ciò premesso, nelle ipotesi (5), il sistema (4) si può scrivere sotto la seguente forma:

e si vede facilmente che questo sistema, e quindi anche il sistema (1), è impossibile, cioè non ammette nessuna soluzione. Basta infatti osservare che la seconda equazione del sistema non può essere soddisfatta da nessun valore della x, essendo per ipotesi b'c-bc'≠0. Si può quindi dire che: se nel sistema (1) sono proporzionali solo i coefficienti delle incognite, il sistema è impossibile.
3° Caso - Si suppone che nel sistema (1) i coefficienti delle incognite e i termini noti delle due equazioni sono fra loro proporzionali, cioè: (6)
si dimostra in tale ipotesi che il sistema è indeterminato.
Dalla (6) si ricava ab'-a'b=0, bc'-b'c=0, perciò il sistema (4) diventa: (7)

Siccome la seconda uguaglianza delle (7) è un'identità, cioè è soddisfatta da qualsiasi valore attribuito alla x, il sistema (7), e quindi anche il sistema (1), ammette come soluzioni tutte e solo le soluzioni della prima equazione del sistema che, come è noto, sono infinite. Il sistema, ammettendo infinite soluzioni, è indeterminato.
Si può quindi dire che: se nel sistema (1) i coefficienti delle incognite ed i termini noti delle due equazioni sono fra loro proporzionali, comprendendo nella proporzionalità anche il caso in cui i due termini noti siano nulli, il sistema è indeterminato e le sue soluzioni sono tutte e sole le soluzioni di una qualsiasi delle due equazioni.
cioè nell'ipotesi che i coefficienti delle incognite di egual nome delle due equazioni, non siano fra loro proporzionali. In tal caso si è visto che l'unica soluzione del sistema è data da: (8)
Per ricordare a memoria le formule (8), si introduce il simbolo di matrice. Se α, β, γ, δ, sono 4 numeri qualsiasi, si chiama matrice quadrata del 2° ordine il seguente simbolo: (1)

Si chiama determinante del 2° ordine, rappresentato dalla matrice (1) e si indica con il simbolo:
il numero: αδ-βγ, cioè si pone per definizione:
Esempi:
Pertanto, si ha anche la regola pratica per determinare effettivamente questa soluzione.
Premesso ciò, si vede che le formule (8) si possono scrivere sotto la forma seguente:

Esempi:
1)-risolvere il sistema:

In questo caso risulta: (9) a=3, b=-2, c=-7, a'=2, b'=7, c'=37, ed i coefficienti delle incognite non sono proporzionali. Il sistema ammette allora una sola soluzione, che si ricava dalle formule (8) sostituendo in esse, alle lettere, i valori (9). Effettuando questa sostituzione si trova:
La soluzione del sistema è quindi: x=1, y=5.
Con l'uso dei determinanti si ha:

2)-il sistema:

è impossibile, perchè i coefficienti delle incognite non sono proporzionali fra loro e non ai termini noti.
3)-il sistema:

è indeterminato, perchè i coefficienti delle incognite e i termini noti sono tutti proporzionali fra loro.
1° - Metodo di riduzione o addizione
Dato il sistema: (1)
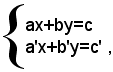
e supposto
si moltiplicano ambo i membri della prima equazione per il numero b' ed ambo i membri della seconda equazione per il numero -b e sommando membro a membro le due equazioni, si ottiene l'equazione: (ab'-a'b)x=b'c-bc'. In modo del tutto analogo, moltiplicando ambo i membri della prima equazione per il numero -a' ed ambo i membri della seconda equazione per il numero a e poi sommando membro a membro le due equazioni, si ottiene l'equazione: (ab'-a'b)y=ac'-a'c. Si ha così il sistema: (2)

che ammette, essendo ab'-a'b≠0, l'unica soluzione:
Siccome la soluzione ottenuta, come è noto, è anche del sistema (1), risolvere il sistema (1),
Esempi:
1)-Risolvere il sistema:

In questo sistema i coefficienti delle incognite non sono proporzionali e perciò esso ammette una ed una sola soluzione.
Per eliminare la y, siccome il m. c. m. dei coefficienti della y è 12, basta moltiplicare ambo i membri della prima equazione per 3 e ambo i membri della seconda equazione per 2 e poi sommare membro a membro le due equazioni, si ha: 9x+12y+10x-12y=54-16, ossia 19x=38, da cui x=2. Moltiplicando ora ambo i membri della prima equazione per 5 e ambo i membri della seconda equazione per -3 e poi sommando membro a membro le due equazioni, si ha: 15x+20y-15x+18y=90+24, ossia 38y=114, da cui y=3. La soluzione del sistema è quindi: x=2, y=3.
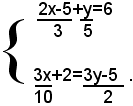
Si riduce il sistema a forma normale, liberando le equazioni dai denominatori, trasportando poi i termini contenenti le incognite nel primo membro e i termini noti nel secondo ed infine riducendo i termini simili, si ha:


In questo sistema i coefficienti delle incognite non sono proporzionali e perciò esso ammette una ed una sola soluzione. Per eliminare la y, siccome il m. c. m. dei coefficienti della y è 15, basta moltiplicare ambo i membri della prima equazione per 5 e ambo i membri della seconda equazione per 3 e poi sommare membro a membro le due equazioni, si ha: 50x+15y+3x-15y=575-45, ossia: 53x=530, da cui: x=10. Per eliminare la x, basta moltiplicare ambo i membri della seconda equazione per -10 e poi sommare membro a membro le due equazioni, si ha: 10x+3y-10x+50y=115+150, ossia: 53y=265, da cui: y=5. La soluzione del sistema è quindi: x=10, y=5.
Dal metodo di addizione si può dedurre la seguente regola:
-per risolvere col metodo di addizione un sistema di due equazioni di primo grado in due incognite, ridotto a forma normale, si moltiplicano ambo i membri delle due equazioni per numeri diversi da zero, tali che i coefficienti di una delle incognite, per esempio y, risultino opposti. Dopo di ciò, sommando membro a membro le due equazioni, si ottiene un'equazione nella sola incognita x, che risolta, dà il valore della x. Con lo stesso procedimento si ricava il valore dell'incognita y.
Metodo di sostituzione
Dato il sistema: (1)
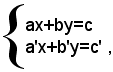
e supposto
si risolve, ad esempio la prima equazione rispetto alla lettera y, e nell'altra equazione si sostituisce a tale incognita l'espressione trovata; si ottiene il sistema: (2)

In tale sistema, la seconda equazione contiene la sola incognita y e, risolvendola si ottiene il valore della x, che sostituito nella prima equazione, dopo facili calcoli, ci fornisce il valore della y e che il sistema (2) ammette la soluzione:
Questa è anche la soluzione del sistema (1), come è noto.
Si
può quindi dire che i due sistemi (1) e (2) sono equivalenti e
perciò, in pratica, per risolvere il sistema (1), basta
risolvere il sistema (2). Questo metodo di risoluzione si
chiama metodo di sostituzione.
Si puà quindi enunciare la seguente regola:
-per risolvere con il metodo di sostituzione un sistema di due equazioni di primo grado in due incognite x, y, ridotto a forma normale, si procede come segue:
1)-si risolve una delle due equazioni rispetto ad un'incognita, ad esempio la y;
2)-si sostituisce l'espressione così trovata al posto della y nell'altra equazione;
3)-si risolve questa equazione rispetto all'incognita x e si determina il valore di questa incognita;
4)-il valore della y si ottiene sostituendo il valore della x nella rispettiva espressione trovata in precedenza.
Esempi:
1)-risolvere il sistema:

Il sistema è già scritto sotto forma normale e, non essendo proporzionali i coefficienti delle incognite, esso ammette una sola soluzione. Ricavando la y dalla prima equazione e sostituendo tale espressione al posto della y nella seconda equazione, si ha il sistema equivalente:

Si puà quindi enunciare la seguente regola:
-per risolvere con il metodo di sostituzione un sistema di due equazioni di primo grado in due incognite x, y, ridotto a forma normale, si procede come segue:
1)-si risolve una delle due equazioni rispetto ad un'incognita, ad esempio la y;
2)-si sostituisce l'espressione così trovata al posto della y nell'altra equazione;
3)-si risolve questa equazione rispetto all'incognita x e si determina il valore di questa incognita;
4)-il valore della y si ottiene sostituendo il valore della x nella rispettiva espressione trovata in precedenza.
Esempi:
1)-risolvere il sistema:

Il sistema è già scritto sotto forma normale e, non essendo proporzionali i coefficienti delle incognite, esso ammette una sola soluzione. Ricavando la y dalla prima equazione e sostituendo tale espressione al posto della y nella seconda equazione, si ha il sistema equivalente:

ossia:

o anche:

cioè:

Sostituendo, nella prima equazione, ad x il valore trovato, si ha:
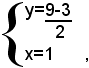
ossia:

La soluzione del sistema è quindi: x=1, y=3.
2)-risolvere il sistema:

Si riduce il sistema sotto forma normale, liberando le equazioni dai denominatori, trasportando nel primo membro i termini contenenti le incognite e i termini noti nel secondo e riducendo i termini simili, si ottiene:

cioè un sistema in cui i coefficienti delle incognite non sono proporzionali. Ricavando la y dalla prima equazione e sostituendo l'espressione trovata al posto della y nella seconda equazione, si ha:

da cui, risolvendo la seconda equazione, si ha:

e quindi:

La soluzione del sistema è quindi: x=4, y=10.
Metodo del confronto
Per risolvere col metodo del confronto un sistema di due equazioni di primo grado in due incognite, ridotto a forma normale, bisogna innanzitutto osservare che questo è un caso particolare del metodo di sostituzione. Precisamente, mentre con il metodo di sostituzione si risolveva una sola delle due equazioni rispetto ad un'incognita, ora si risolvono le due equazioni rispetto alla stessa incognita.
Esempio: risolvere il sistema:

nel quale i coefficienti delle incognite non sono proporzionali. Risolvendo entrambe le equazioni rispetto alla y, si ottiene il seguente sistema:

che è equivalente a quello assegnato. Sostituendo, nella seconda equazione, al posto della y, l'espressione data dalla prima equazione, si ha il sistema equivalente seguente:

nel quale la seconda equazione contiene la sola incognita x. Risolvendo la seconda equazione, si trova il sistema:

da cui, sostituendo nella prima equazione il valore trovato della x, risulta:
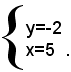
La soluzione del sistema è quindi: x=5, y=-2.
Nota bene
I procedimenti indicati per risolvere i sistemi di due equazioni di primo grado in due incognite, con i coefficienti numerici, si prestano anche per risolvere i sistemi interi di primo grado a coefficienti letterali, oppure i sistemi fratti che, ridotti a forma normale, danno luogo ad un sistema di primo grado. Nel primo caso, cioè quando i coefficienti sono letterali, bisogna escludere, per le lettere, quegli eventuali particolari valori che fanno perdere di significato ad almeno una delle due equazioni del sistema. Si dovrà poi anche vedere se esistono dei particolari valori delle lettere per i quali il sistema diventa impossibile o indeterminato. Nel secondo caso invece, poichè per trasformare il sistema fratto a forma normale, si devono moltiplicare ambo i membri delle equazioni per un'espressione contenente almeno un'incognita, potrebbe capitare che il sistema così ottenuto avesse più soluzioni di quello assegnato, analogamente a quanto visto per le equazioni fratte. Perciò, dopo aver risolto questo secondo sistema, occorrerà sempre appurare se le soluzioni trovate soddisfano, oppure no, anche il sistema assegnato. Per far ciò, basterà solamente verificare se i valori trovati annullano o no i denominatori che compaiono nel sistema dato, come già si è visto nel caso di una sola equazione.
Esempi:
1)-risolvere il sistema:
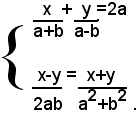
Si liberano dapprima le equazioni dai denominatori, perciò si devono moltiplicare ambo i membri della prima equazione per (a+b)(a-b) ed ambo i membri della seconda per 2ab(a2+b2), dopo aver supposto (1) a≠-b, a≠b, a≠0, b≠0. Dopo facili calcoli, si ha: (2)

Bisogna osservare che, nelle ipotesi (1) i coefficienti delle variabili del sistema (2), non sono fra loro proporzionali, perciò il sistema ammette una ed una sola soluzione. Si risolve ora il sistema con il metodo di addizione e, a tale scopo, si moltiplicano ambo i membri della prima equazione per (a+b) e si sommano membro a membro le due equazioni, si ottiene:
(a-b)(a+b)x+(a-b)2x=2a(a2-b2)(a+b), ossia, dividendo ambo i membri per a-b, che è un numero diverso da zero, si ha: (a+b)x+(a-b)x=2a(a+b)(a-b), cioè: 2ax=2a(a+b)2; da cui, essendo a≠0, si ha: x=(a+b)2. Se invece si moltiplicano ambo i membri della prima equazione del sistema (2) per -(a-b) e poi si sommano membro a membro le due equazioni del sistema, si ha: y=(a-b)2. Pertanto, nelle ipotesi (1), il sistema dato ammette una ed una sola soluzione data da x=(a+b)2, y=(a-b)2.
2)-risolvere il sistema:
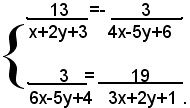
Questo è un sistema fratto; liberando le equazioni dai denominatori, si ottiene il sistema:

ossia, dopo facili semplificazioni:
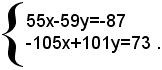
Risolvendo il sistema con uno qualsiasi dei metodi trattati, si ottiene: x=7, y=8, che è anche una soluzione del sistema (1), dato che per tali valori, non si annulla nessun denominatore del sistema dato.
3)-risolvere il sistema:

Liberando le equazioni dai denominatori, dopo facili calcoli, si ottiene:

Risolvendo il sistema, si trova x=2, y=3. Questa soluzione non soddisfa però il sistema dato, perchè, per x=2, si annulla il denominatore della prima equazione. Perciò, il sistema considerato è impossibile.
Risoluzione dei sistemi di tre o più equazioni di primo grado con altrettante incognite
I metodi di risoluzione, trattati per i sistemi di due equazioni di primo grado in due incognite, si possono applicare anche ai sistemi di tre o più equazioni di primo grado con altrettante incognite. Si vede ora come si deve procedere su un esempio.
Risolvere il seguente sistema, scritto sotto forma normale: (1)

Risoluzione con il metodo di sostituzione
Si ricava, ad esempio, il valore della x dalla prima equazione e lo si sostituisce, al posto della x nelle altre due equazioni, ottenendo così il sistema:

ossia, dopo facili semplificazioni:

Risolvendo il sistema formato dalle ultime due equazioni, nelle incognite y e z, si ha:

Sostituendo ora, nella prima equazione, ad y e z i valori trovati, si ha:
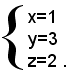
L'unica soluzione del sistema è quindi: x=1, y=3, z=2.
Risoluzione con il metodo di confronto
Risolvendo le tre equazioni del sistema (1) rispetto, ad esempio, alla x, si ottiene il sistema:
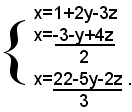
Sostituendo, nella seconda e terza equazione, al posto della x, l'espressione data dalla prima equazione, si ottiene il sistema:
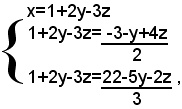
nel quale le ultime due equazioni contengono le due sole incognite y e z. Risolvendo il sistema formato da queste due ultime equazioni, con facili calcoli si trova:

Evidentemente, si ha:
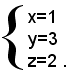
Tale soluzione è la stessa di quella trovata con il metodo di sostituzione.
Risoluzione con il metodo di addizione
Fra le prime due equazioni del sistema (1), si elimina, ad esempio, la x, moltiplicando ambo i membri della prima equazione per -2 e poi sommando membro a membro le due equazioni, si ottiene: -2x+4y-6z+2x+y-4z=-2-3, ossia: y-2z=-1. Si elimina ora la x tra la prima e la terza equazione, moltiplicando ambo i membri della prima equazione per -3 e poi sommando membro a membro le due equazioni. Con facili calcoli si trova: 11y-7z=19. Risolvendo ora, con un metodo qualsiasi, il sistema:

si trova y=3, z=2. Sostituendo questi valori, al posto, rispettivamente di y e z, in una qualsiasi delle equazioni del sistema (1), si trova x=1. Perciò, x=1, y=3, z=2 è l'unica soluzione del sistema dato.
Problemi di primo grado a più incognite
Si considerano ora alcuni problemi che si traducono in due o più equazioni di primo grado con altrettante incognite.
1)-Si trovi la frazione che diventa uguale a 1/3, quando si aggiunge 1 al numeratore, ed uguale a 1/4, quando invece si aumenta di 1 il denominatore.
Si indica con x il numeratore della frazione cercata e con y il denominatore. I numeri x e y devono essere quindi numeri interi. La prima condizione data dal problema si traduce nella seguente equazione:
mentre la seconda condizione, si traduce nell'equazione:
Il problema perciò si si traduce nel seguente sistema fratto: (1)

Liberando le equazioni del sistema dai denominatori, si ottiene:

e dopo facili calcoli risulta x=4, y=15, quindi la frazione cercata è 4/15.
2)-Si ha la somma di € 39500, costituita da banconote di € 500, € 1000, € 5000. Il doppio delle banconote da € 500 aumentato del numero delle banconote da € 1000, dà il numero delle banconote da € 5000, aumentato di 5. Il quintuplo delle banconote da € 5000, diminuito del triplo delle banconote da € 1000, dà il quadruplo delle banconote da € 500 aumentato di 9. Trovare il numero delle banconote di ciascuna specie.
Si indicano con x, y, z, rispettivamente i numeri dei biglietti da € 500, € 1000, € 5000. Poichè l'ammontare della somma è € 39500, deve risultare: 500x+1000y+5000z=€ 39500. Per la seconda condizione del problema, si ha: 2x+y=z+5, e per la terza condizione, risulta: 5z-3y=4x+9. Il problema si traduce quindi nel sistema:

e, dopo semplificazioni, diventa:
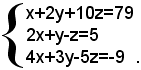
Si risolve ora il sistema con il metodo di sostituzione: si ricava il valore della y dalla seconda equazione, e lo si sostituisce, al posto della y, nelle altre due equazioni, si ottiene:

Risolvendo il sistema formato dalle due ultime equazioni nelle incognite x e z, con un metodo qualsiasi, si ha: x=5, z=7. Sostituendo questi valori al posto, rispettivamente della x e della y, nella prima equazione, si ricava y=2. Perciò la soluzione del sistema è x=5, y=2, z=7.
3)-Calcolare le misure dei lati di un rettangolo, sapendo che se si aumenta l'altezza di m 3 e si diminuisce di altrettanto la base, l'area del rettangolo non cambia. Invece se si aumenta l'altezza di m 5 e si diminuisce la base di m 3, la superficie del rettangolo aumenta di 16 m2. Si indica con x la misura dell'altezza e con y quella della base del rettangolo; l'area è data da xy. Se si aumenta l'altezza di m 3 e si diminuisce la base di altrettanto, l'area del nuovo rettangolo è (x+3)(y-3), perciò, per la prima condizione del problema, si può scrivere l'equazione: (x+3)(y-3)=xy. Analogamente, per la seconda condizione del problema, si può scrivere anche l'equazione: (x+5)(y-3)=xy+16. Il problema si traduce quindi nel seguente sistema:

e, dopo semplificazioni, diventa:

Risolvendo questo sistema, con un metodo qualsiasi, si trova che esso ammette la seguente soluzione: x=8, y=11. Perciò, la misura dell'altezza del rettangolo è 8, mentre quella della base è 11.