OPERAZIONI SUGLI INSIEMI ---> INDICE
Unione o riunione di insiemi
Si chiama unione di due insiemi A e B, l'insieme degli elementi che appartengono ad A oppure a B. La condizione "oppure" ha il senso di "indifferentemente". Tale unione si indica con il simbolo
e quella dei due insiemi con
A B;
in altri termini, per definizione si ha:
logicamente risulta
Quando si costruisce l'unione di due insiemi A e B, si considerano gli elementi di A che non appartengono a B, quelli di B che non appartengono ad A e quelli che appartengono ad A e B.
Da notare che nella definizione data non è escluso che sia A=B.
Siano A e B due parti qualsiasi dell'insieme E, cioè rispettivamente:
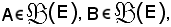
si ha
Inoltre, quale che sia
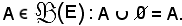
Intersezione di insiemiSi
chiama intersezione di due insiemi A e B, l'insieme degli elementi
che appartengono ad A ed a B. Tale intersezione si indica con il simbolo
e quella dei due insiemi con
A B;
in altri termini, per definizione si ha:
x
A B 
xA 
xB;
logicamente risulta
A B = B A.
Da notare che nella definizione data non è escluso che sia A=B.
Inoltre, considerato l'insieme E, quale che sia
Si osserva inoltre che l'intersezione di A e B è contenuta nella riunione di A e B, cioè:
A B 
A B.
Insiemi disgiunti
(
xAB).
Se l'intersezione dei due insiemi A e B non è vuota, cioè se
A B ≠ 
,
i due insiemi hanno elementi in comune.
Complementare di un insieme
Sia E un insieme ed X una sua parte, cioè se
gli elementi di E non appartenenti ad X costituiscono una parte di E denominata complementare di X rispetto o relativamente ad E, indicata con il simbolo
In altri termini, per definizione si ha:
Equivalentemente si può scrivere
In tema di notazioni e terminologia, ogni qualvolta non vi sia il rischio di equivoci, il complementare di X rispetto ad E si può più semplicemente indicare con
e chiamare, "tout-court", complementare di X, senza precisare "rispetto ad E".
Inoltre, invece di tali notazioni, si usa anche il termine "differenza":
E - X.
Logicamente si ha:
Proprietà e relazioni fra unione ed intersezione
L'unione e l'intersezione considerate come operazioni sugl'insiemi X, Y, Z, godono, rispettivamente, delle seguenti proprietà:
La dimostrazione deriva dalle definizioni di unione, intersezione ed inclusione.
Nota bene
La 1) esprime che l'unione dell'insieme X con se stesso è uguale ad X, mentre la 1') che l'intersezione di X con se stesso è uguale ad X.
La 2) e la 2') esprimono che la riunione e l'intersezione e godono rispettivamente della proprietà associativa.
La 3) e la 3') esprimono che la riunione e l'intersezione godono rispettivamente della proprietà commutativa.
La 4) esprime che l'insieme X, oppure l'insieme Y, è contenuto nella loro riunione, in quanto tutti gli elementi di X o di Y appartengono alla loro riunione, mentre la 4') esprime che l'intersezione è contenuta in entrambi gl'insiemi, in quanto tutti gli elementi dell'intersezione di X e Y sono elementi comuni ad X e ad Y.
La 5) esprime che se gl'insiemi X ed Y sono entrambi contenuti nell'insieme Z, la loro riunione è anch'essa contenuta in Z, mentre la 5') esprime che se l'insieme Z è contenuto sia nell'insieme X che nell'insieme Y, Z è anche contenuto nell'intersezione di X ed Y.
La 6) esprime la riunione sotto forma di inclusione, pertanto, se X è contenuto in Y, cioè gli elementi di X sono tutti elementi di Y, l'unione di X ed Y è uguale ad Y, mentre la 6') esprime che l'intersezione di X ed Y è uguale ad X, in quanto tutti gli elementi di X appartengono ad Y.
La 7) esprime la proprietà distributiva dell'intersezione rispetto alla riunione, mentre la 7') esprime la proprietà distributiva della riunione rispetto all'intersezione.
Proprietà e relazioni fra unione, intersezione e complementare
Se X e Y sono parti dell'insieme E, si ha:
La dimostrazione deriva dalle definizioni di unione, intersezione, inclusione e complementare.
Nota bene
La 1) esprime la proprietà involutoria o l'involutarietà del complementare, cioè il complementare del complementare di X è X stesso.
Per dimostrare la 2) si prende un elemento
per definizione di complementare a appartiene ad E e non appartiene nè ad X nè ad Y, cioè
Pertanto
cioè a è un elemento comune ai due complementari suddetti, perciò è elemento della loro intersezione.
Per dimostrare la 3) si prende un elemento
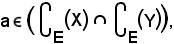
per il significato di intersezione
Da ciò si deduce che
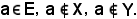
Siccome l'elemento a non appartiene nè ad X e nè ad Y, esso non appartiene alla loro riunione, cioè
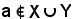
e per definizione di complementare
Per dimostrare la 4), si deve tener conto che ogni elemento del complementare non appartiene ad X, quindi l'intersezione di X con il suo complementare è l'insieme vuoto.
Per dimostrare la 5), si considerano i rispettivi complementari, ottenendo:
Inoltre, risulta anche
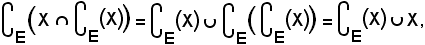
per la proprietà 3) e per la proprietà involutoria del complementare, quindi, essendo uguali i primi membri delle due uguaglianze suddette, si conclude che la 5) è vera.
Per dimostrare la 6), cioè, dire che l'intersezione di X e Y è uguale all'insieme vuoto equivale a dire che X è contenuto nel complementare di Y rispetto ad E.
Infatti, preso un elemento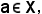
poichè l'intersezione di X ed Y è uguale all'insieme vuoto,
perciò
Il viceversa è ovvio.
Per dimostrare la 7), cioè, dire che la riunione fra X ed Y è uguale all'insieme E equivale a dire che il complementare di Y rispetto ad E è contenuto in X.
La dimostrazione è ovvia.
E' immediato riconoscere ora che le proprietà 5) e 4) sopra menzionate determinano univocamente il complementare di X rispetto ad E, nel senso che se X ed Y sono parti di E tale che sia
allora necessariamente risulta
In altri termini:
Inoltre, si riconosce che se A è una parte dell'insieme E, cioè
e se X è una parte di A, cioè
risulta
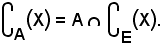
Traccia di una parte di un insieme su un'altra parte dello stesso insieme
Se A è una parte dell'insieme E, per ogni altra parte X di E, si chiama traccia di X su A e s'indica con XA l'intersezione di A con X, cioè:
XA = A X.
Se Y è un'ulteriore parte di E, considerata la traccia YA di Y su A, si riconosce facilmente che:
In generale, si può dire che se s'indica con
, ics gotica, un insieme di parti di E, la traccia di su A, indicata con
è l'insieme delle parti di A che sono traccia su A di elementi di.
Si chiama unione di due insiemi A e B, l'insieme degli elementi che appartengono ad A oppure a B. La condizione "oppure" ha il senso di "indifferentemente". Tale unione si indica con il simbolo
e quella dei due insiemi con
A
B;in altri termini, per definizione si ha:
xA B xA v xB;
A B xA v xB;logicamente risulta
A B = B A.
B = B A.Quando si costruisce l'unione di due insiemi A e B, si considerano gli elementi di A che non appartengono a B, quelli di B che non appartengono ad A e quelli che appartengono ad A e B.
Da notare che nella definizione data non è escluso che sia A=B.
Siano A e B due parti qualsiasi dell'insieme E, cioè rispettivamente:
si ha
Inoltre, quale che sia
Intersezione di insiemi
e quella dei due insiemi con
A
B;in altri termini, per definizione si ha:
x
A B xA xB;logicamente risulta
A
B = B A.Da notare che nella definizione data non è escluso che sia A=B.
Inoltre, considerato l'insieme E, quale che sia
Si osserva inoltre che l'intersezione di A e B è contenuta nella riunione di A e B, cioè:
B A B.Insiemi disgiunti
Si dice che gl'insiemi A e B sono disgiunti se non hanno elementi in comune, cioè se risulta
A B = ,
equivalentemente si può scrivere
B = ,equivalentemente si può scrivere
( xAB).Se l'intersezione dei due insiemi A e B non è vuota, cioè se
A
B ≠ ,i due insiemi hanno elementi in comune.
Complementare di un insieme
Sia E un insieme ed X una sua parte, cioè se
gli elementi di E non appartenenti ad X costituiscono una parte di E denominata complementare di X rispetto o relativamente ad E, indicata con il simbolo
In altri termini, per definizione si ha:
Equivalentemente si può scrivere
In tema di notazioni e terminologia, ogni qualvolta non vi sia il rischio di equivoci, il complementare di X rispetto ad E si può più semplicemente indicare con
e chiamare, "tout-court", complementare di X, senza precisare "rispetto ad E".
Inoltre, invece di tali notazioni, si usa anche il termine "differenza":
E - X.
Logicamente si ha:
Proprietà e relazioni fra unione ed intersezione
L'unione e l'intersezione considerate come operazioni sugl'insiemi X, Y, Z, godono, rispettivamente, delle seguenti proprietà:
La dimostrazione deriva dalle definizioni di unione, intersezione ed inclusione.
Nota bene
La 1) esprime che l'unione dell'insieme X con se stesso è uguale ad X, mentre la 1') che l'intersezione di X con se stesso è uguale ad X.
La 2) e la 2') esprimono che la riunione e l'intersezione e godono rispettivamente della proprietà associativa.
La 3) e la 3') esprimono che la riunione e l'intersezione godono rispettivamente della proprietà commutativa.
La 4) esprime che l'insieme X, oppure l'insieme Y, è contenuto nella loro riunione, in quanto tutti gli elementi di X o di Y appartengono alla loro riunione, mentre la 4') esprime che l'intersezione è contenuta in entrambi gl'insiemi, in quanto tutti gli elementi dell'intersezione di X e Y sono elementi comuni ad X e ad Y.
La 5) esprime che se gl'insiemi X ed Y sono entrambi contenuti nell'insieme Z, la loro riunione è anch'essa contenuta in Z, mentre la 5') esprime che se l'insieme Z è contenuto sia nell'insieme X che nell'insieme Y, Z è anche contenuto nell'intersezione di X ed Y.
La 6) esprime la riunione sotto forma di inclusione, pertanto, se X è contenuto in Y, cioè gli elementi di X sono tutti elementi di Y, l'unione di X ed Y è uguale ad Y, mentre la 6') esprime che l'intersezione di X ed Y è uguale ad X, in quanto tutti gli elementi di X appartengono ad Y.
La 7) esprime la proprietà distributiva dell'intersezione rispetto alla riunione, mentre la 7') esprime la proprietà distributiva della riunione rispetto all'intersezione.
Proprietà e relazioni fra unione, intersezione e complementare
Se X e Y sono parti dell'insieme E, si ha:
La dimostrazione deriva dalle definizioni di unione, intersezione, inclusione e complementare.
Nota bene
La 1) esprime la proprietà involutoria o l'involutarietà del complementare, cioè il complementare del complementare di X è X stesso.
Per dimostrare la 2) si prende un elemento
per definizione di complementare a appartiene ad E e non appartiene nè ad X nè ad Y, cioè
Pertanto
cioè a è un elemento comune ai due complementari suddetti, perciò è elemento della loro intersezione.
Per dimostrare la 3) si prende un elemento
per il significato di intersezione
Da ciò si deduce che
Siccome l'elemento a non appartiene nè ad X e nè ad Y, esso non appartiene alla loro riunione, cioè
e per definizione di complementare
Per dimostrare la 4), si deve tener conto che ogni elemento del complementare non appartiene ad X, quindi l'intersezione di X con il suo complementare è l'insieme vuoto.
Per dimostrare la 5), si considerano i rispettivi complementari, ottenendo:
Inoltre, risulta anche
per la proprietà 3) e per la proprietà involutoria del complementare, quindi, essendo uguali i primi membri delle due uguaglianze suddette, si conclude che la 5) è vera.
Per dimostrare la 6), cioè, dire che l'intersezione di X e Y è uguale all'insieme vuoto equivale a dire che X è contenuto nel complementare di Y rispetto ad E.
Infatti, preso un elemento
poichè l'intersezione di X ed Y è uguale all'insieme vuoto,perciò
Il viceversa è ovvio.
Per dimostrare la 7), cioè, dire che la riunione fra X ed Y è uguale all'insieme E equivale a dire che il complementare di Y rispetto ad E è contenuto in X.
La dimostrazione è ovvia.
E' immediato riconoscere ora che le proprietà 5) e 4) sopra menzionate determinano univocamente il complementare di X rispetto ad E, nel senso che se X ed Y sono parti di E tale che sia
allora necessariamente risulta
In altri termini:
Inoltre, si riconosce che se A è una parte dell'insieme E, cioè
e se X è una parte di A, cioè
risulta
Traccia di una parte di un insieme su un'altra parte dello stesso insieme
Se A è una parte dell'insieme E, per ogni altra parte X di E, si chiama traccia di X su A e s'indica con XA l'intersezione di A con X, cioè:
X.Se Y è un'ulteriore parte di E, considerata la traccia YA di Y su A, si riconosce facilmente che:
In generale, si può dire che se s'indica con
, ics gotica, un insieme di parti di E, la traccia di su A, indicata con è l'insieme delle parti di A che sono traccia su A di elementi di
.