FASCI DI PIANI ---> INDICE
Definizione
- Si
chiama fascio proprio di piani l'insieme dei piani dello spazio
contenenti una retta assegnata definita asse del fascio.
Il fascio proprio s'indica con
p.
Definizione - Si chiama fascio improprio di piani l'insieme dei piani paralleli ad un piano assegnato.
Il fascio improprio s'indica coni.
Rappresentazioni analitiche
Siano assegnati i piani π e π', rispettivamente di equazioni
ax + by + cz + d = 0, a'x + b'y + c'z + d' = 0,
cioè l'asse del fascio proprio è determinato dalla retta d'intersezione dei due piani.
Ciò detto, si dimostra che:
-ogni piano avente equazione combinazione lineare delle equazioni di π e π' secondo due fattori di proporzionalità non nulli, λ e μ, è un piano del fascio proprio considerato, e viceversa, cioè
σ
p 
(λ, μ)R 
R, (λ, μ) ≠ (0, 0) 
λ(ax + by + cz + d) + μ(a'x + b'y + c'z + d') = 0,
equazione di σ.
La condizione è necessaria.
Se
(λ, μ) ≠ (0, 0),
e se si combinano le due equazioni, si vuol vedere se si ottiene un'equazione di primo grado.
Si suppone, ad esempio, che se nelle seguenti espressioni, indicate con *),
λa + μa' = 0,
λb + μb' = 0,
λc + μc' = 0,
a, b, c, sono proporzionali ad a', b', c', e viceversa, si ha:
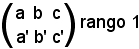
e ciò smentisce l'ipotesi, quindi le *) non possono essere simultaneamente nulle, si ha pertanto l'equazione di un piano.
La condizione è sufficiente.
Se
pr = π 
π',
cioè le coordinate di P(x0, y0, z0) costituiscono una soluzione del sistema precedente, tale che
ax0 + by0 + cz0 + d = 0, a'x0 + b'y0 + c'z + d' = 0.
Si dimostra ora che
Pr 
Pσ.
Infatti, si consideri:
λ(ax0 + by0 + cz0 + d) + μ(a'x0 + b'y0 + c'z0 + d') = λ0 + μ0 Pσ
Pr = π π' : Pσ σp.
Si supponga ora che la retta r sia comune ai due piani, cioè
r = π π',
e si consideri il punto P0σ, P0
r.
Si indica con
l(x0, y0, z0) = ax0 + by0 + cz0 + d
l'(x0, y0, z0) = a'x0 + b'y0 + c'z0 + d',
λ = l'(x0, y0, z0) e μ = -l(x0, y0, z0);
questi sono nulli, perchè P0 non appartiene contemporaneamente a π e π', quindi le coordinate non sono soluzioni del sistema, cioè non sono contemporaneamente nulle, quindi un'equazione combinazione lineare delle due equazioni, secondo λ e μ non entrambi nulli, rappresenta l'equazione del fascio.
Essendo
l'(x0, y0, z0)(ax + by + cz + d) - l'(x0, y0, z0)(a'x + b'y + c'z + d') = 0,
l(x0, y0, z0)l(x0, y0, z0) - l(x0, y0, z0)l(x0, y0, z0) = 0.
Per il fascio improprio si fanno dimostrazioni analoghe:
πi, π'i, π ≠ π', σi (λ, μ)R R (λa + μa', λb + μb, λc + μc') ≠ (0, 0, 0)
λ(ax + by + cz + d) + μ(a'x + b'y + c'z + d')= 0. (*)
Ovviamente, se si considera il fascio generico:
π, π', π ≠ π', σ (λ, μ)R R siano verificate le condizioni (*).
Altre condizioni.
Siano π, π', π'' tre piani appartenenti allo stesso fascio, di cui due di essi distinti:
π) ax + by + cz + d = 0,
π') a'x + b'y + c'z + d' = 0,
π'') a''x + b''y + c''z + d'' = 0,
ciò equivale a dire che
Siano π, π', π'' tre piani appartenenti allo stesso fascio, di cui due di essi distinti.
Si consideri π'', determinato da π e π', di equazione
(λa + μa')x + (λb + μb')y + (λc + μc')z + (λd + μd') = 0,
quindi
La condizione è quindi necessaria, si dimostra ora che è anche sufficiente.
Si suppone che il rango sia due, il che vuol dire che i due piani sono distinti.
D'altronde non tutti i minori del secondo ordine sono nulli, mentre lo sono quelli del terzo ordine, cioè
pertanto due dei tre piani sono distinti ed uno dei tre è combinazione lineare di due.
Il fascio proprio s'indica con
p.Definizione - Si chiama fascio improprio di piani l'insieme dei piani paralleli ad un piano assegnato.
Il fascio improprio s'indica con
i.Rappresentazioni analitiche
Siano assegnati i piani π e π', rispettivamente di equazioni
ax + by + cz + d = 0, a'x + b'y + c'z + d' = 0,
cioè l'asse del fascio proprio è determinato dalla retta d'intersezione dei due piani.
Ciò detto, si dimostra che:
-ogni piano avente equazione combinazione lineare delle equazioni di π e π' secondo due fattori di proporzionalità non nulli, λ e μ, è un piano del fascio proprio considerato, e viceversa, cioè
σ
p (λ, μ)R R, (λ, μ) ≠ (0, 0) λ(ax + by + cz + d) + μ(a'x + b'y + c'z + d') = 0,equazione di σ.
La condizione è necessaria.
Se
(λ, μ) ≠ (0, 0),
e se si combinano le due equazioni, si vuol vedere se si ottiene un'equazione di primo grado.
Si suppone, ad esempio, che se nelle seguenti espressioni, indicate con *),
λa + μa' = 0,
λb + μb' = 0,
λc + μc' = 0,
a, b, c, sono proporzionali ad a', b', c', e viceversa, si ha:
e ciò smentisce l'ipotesi, quindi le *) non possono essere simultaneamente nulle, si ha pertanto l'equazione di un piano.
La condizione è sufficiente.
Se
p
r = π π',cioè le coordinate di P(x0, y0, z0) costituiscono una soluzione del sistema precedente, tale che
ax0 + by0 + cz0 + d = 0, a'x0 + b'y0 + c'z + d' = 0.
Si dimostra ora che
P
r Pσ.Infatti, si consideri:
λ(ax0 + by0 + cz0 + d) + μ(a'x0 + b'y0 + c'z0 + d') = λ0 + μ0
Pσ Pr = π π' : Pσ σp.Si supponga ora che la retta r sia comune ai due piani, cioè
r = π
π',e si consideri il punto P0
σ, P0r.Si indica con
l(x0, y0, z0) = ax0 + by0 + cz0 + d
l'(x0, y0, z0) = a'x0 + b'y0 + c'z0 + d',con
λ = l'(x0, y0, z0) e μ = -l(x0, y0, z0);
questi sono nulli, perchè P0 non appartiene contemporaneamente a π e π', quindi le coordinate non sono soluzioni del sistema, cioè non sono contemporaneamente nulle, quindi un'equazione combinazione lineare delle due equazioni, secondo λ e μ non entrambi nulli, rappresenta l'equazione del fascio.
Essendo
l'(x0, y0, z0)(ax + by + cz + d) - l'(x0, y0, z0)(a'x + b'y + c'z + d') = 0,
l(x0, y0, z0)l(x0, y0, z0) - l(x0, y0, z0)l(x0, y0, z0) = 0.
Per il fascio improprio si fanno dimostrazioni analoghe:
π
i, π'i, π ≠ π', σi (λ, μ)R R (λa + μa', λb + μb, λc + μc') ≠ (0, 0, 0) λ(ax + by + cz + d) + μ(a'x + b'y + c'z + d')= 0. (*)Ovviamente, se si considera il fascio generico
:π
, π', π ≠ π', σ (λ, μ)R R siano verificate le condizioni (*).Altre condizioni.
Siano π, π', π'' tre piani appartenenti allo stesso fascio, di cui due di essi distinti:
π) ax + by + cz + d = 0,
π') a'x + b'y + c'z + d' = 0,
π'') a''x + b''y + c''z + d'' = 0,
ciò equivale a dire che
Siano π, π', π'' tre piani appartenenti allo stesso fascio, di cui due di essi distinti.
Si consideri π''
, determinato da π e π', di equazione(λa + μa')x + (λb + μb')y + (λc + μc')z + (λd + μd') = 0,
quindi
La condizione è quindi necessaria, si dimostra ora che è anche sufficiente.
Si suppone che il rango sia due, il che vuol dire che i due piani sono distinti.
D'altronde non tutti i minori del secondo ordine sono nulli, mentre lo sono quelli del terzo ordine, cioè
pertanto due dei tre piani sono distinti ed uno dei tre è combinazione lineare di due.