RETTE E SEGMENTI ---> INDICE
Postulato dell'ordine della retta euclidea
Si dice che su una retta r è stato fissato un verso, se è stabilita una relazione tra coppie di punti (A, B) della retta per cui un punto precede l'altro. Questa relazione è detta verso e significa che A e B sono due punti della retta r. Se si dice che A precede B, s'introduce il verso indicato nella seguente figura.

Proprietà
3)-Se su una retta si prendono due punti qualsiasi, si possono introdurre due relazioni, ossia due versi, il primo quando A precede B e l'altro quando B precede A.
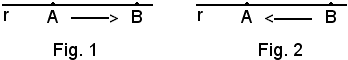
Il primo verso, Fig. 1, si ha quando un punto si sposta da A a B e segue il senso della freccia; il secondo verso, Fig. 2, si ha quando un punto si sposta da B ad A e segue il senso della freccia. In tal modo sono stati fissati due versi, uno opposto all'altro.
Postulato
Si dice che su una retta r è stato fissato un verso, se è stabilita una relazione tra coppie di punti (A, B) della retta per cui un punto precede l'altro. Questa relazione è detta verso e significa che A e B sono due punti della retta r. Se si dice che A precede B, s'introduce il verso indicato nella seguente figura.
Proprietà
1)-Se
su una retta si hanno tre punti A, B, C, e si è stabilito che A precede
B e che B precede C, allora si può asserire che A precede C.
2)-Se su una retta si hanno due punti A, B, e si è stabilito che A precede B e che B precede A, allora si può asserire che A e B coincidono.
2)-Se su una retta si hanno due punti A, B, e si è stabilito che A precede B e che B precede A, allora si può asserire che A e B coincidono.
3)-Se su una retta si prendono due punti qualsiasi, si possono introdurre due relazioni, ossia due versi, il primo quando A precede B e l'altro quando B precede A.
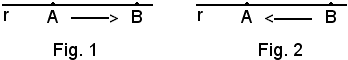
Il primo verso, Fig. 1, si ha quando un punto si sposta da A a B e segue il senso della freccia; il secondo verso, Fig. 2, si ha quando un punto si sposta da B ad A e segue il senso della freccia. In tal modo sono stati fissati due versi, uno opposto all'altro.
Postulato
Dati
una retta r e due punti A e B distinti su di essa, cioè A ≠ B, e
stabilito un verso, esiste un punto C diverso da A e da B, cioè C ≠ A e C ≠ B, tale che A precede C e C precede B.
Ciò significa che fra due punti distinti A e B esistono sempre altri punti interni ad essi, pertanto si definisce segmento di estremi A e B l'insieme di tali punti, compresi A e B.
Postulato della continuità o di Dedekind
Si consideri sulla retta euclidea un segmento OP e si supponga di fissare come verso quello quello per cui O precede P. Sia I l'insieme dei punti del segmento OP, esso è suddiviso in due classi:
-la prima classe contiene O,
-la seconda classe contiene P.
Si osserva ora che ogni punto del segmento appartiene ad una sola classe ed ogni punto della prima classe precede ogni punto della seconda classe, cioè esiste un punto A appartenente al segmento OP, ed appartenente ad una sola classe, in modo che ogni punto della seconda classe segue A.
Con ciò si dimostra che, dato un segmento unitario OU, si può costruire un altro segmento OC tale che sia α volte OU, cioè
OC = αOU.
Si consideri una retta r e si fissino su di essa due punti distinti, O ed U, O ≠ U, ed il verso per cui O precede U.
O si chiama origine ed U punto unitario.
E' stato così fissato un riferimento OU, indicato con (O, U).
(O, U).
Si può quindi affermare che esiste una corrispondenza biunivoca senza eccezioni fra i punti della retta ed i numeri reali, cioè esiste una relazione che associa ad ogni punto della retta uno ed un solo numero reale; viceversa, fissato un numero reale appartenente all'insieme dei numeri reali, esiste uno ed un solo punto della retta r che è associato al numero reale.
Si considerano ora i punti della semiretta che contiene il punto U, supposta positiva, mentre quella che non contiene U è supposta negativa; si prende inoltre un punto X ≠ O, ossia si può considerare il segmento OX ed affermare che esiste uno ed un solo numero reale positivo tale che OX risulta multiplo di OU secondo il numero reale α. Si associa cioè al punto X il numero reale positivo α, tale che sia
OX = αOU.
Se invece X coincide con zero, allora al punto O si associa il numero zero dei numeri reali. Ora si considerano i punti X che appartengono alla semiretta negativa, si prende X ≠ O e si associa al punto X il numero reale negativo -α, per cui sia
OX = -αOU.
Ascissa
Il numero associato ad un punto prende il nome di ascissa, ossia α è ascissa di X e si scrive
X(α),
cioè X di ascissa α. L'ascissa dell'origine è 0 e quella del punto unitario è 1.
Se si cambia il riferimento , cambia anche l'ascissa.
, cambia anche l'ascissa.
Segmenti orientati
Si consideri una retta r e si fissino su di essa due punti distinti, X1 ed X2, X1 ≠ X2, che sono estremi del segmento X1X2:

Si considera la coppia formata dagli estremi X1 ed X2 e dal verso secondo cui X1 precede X2.
La coppia di verso X1X2 si chiama segmento orientato.
Due segmenti orientati sono uguali quando le coppie che formano i segmenti hanno primi e secondi membri uguali, cioè per definizione:
X1X2 = X2X3 (segmento di estremi X1X2 = segmento di estremi X2X3)
(segmento di estremi X1X2 = segmento di estremi X2X3)  (verso X1 precede X2 = verso X2 precede X3).
(verso X1 precede X2 = verso X2 precede X3).
Se X1 ed X2 sono due punti ed X1 = X2, X1X2 = X2X1;se X1 ed X2 sono due punti ed X1 ≠ X2, X1X2 ≠ X2X1.
Si considerano due segmenti X1X2 ed X3X4, si dice che essi sono concordi, se il verso secondo il quale X1 precede X2 è lo stesso per cui X3 precede X4; se invece il verso è opposto, si dicono discordi.
Misura del segmento orientato
E' noto come si misura un comune segmento, cioè la misura X1X2, rispetto ad OU, è tale che
X1X2 = αOU.
Per i segmenti orientati, si considera sulla retta r il verso secondo cui O precede U, tale che:
se X1X2 è concorde con OU, si chiama misura del segmento orientato il numero α;
se X1X2 è discorde con OU, si chiama misura del segmento orientato il numero -α.
La misura del segmento orientato si chiama anche distanza orientata di X2 da X1.
Osservazione
Si indica la misura del segmento orientato X1X2 con d12 e la misura del segmento orientato X2X1 con d21, d'altronde risultano:
d12 = α, d21 = -α,
quindi
d12 = -d21,
cioè
d12 + d21 = 0.
Si può dire che:
-comunque si prendano sulla retta due punti X1 ed X2, e si comunque si considerino i due segmenti orientati, la somma delle loro misure è uguale a zero.
Si cerca ora di estendere tale relazione: si prendano sulla retta tre punti X1, X2 ed X3, se questi sono distinti, uno ed uno solo è interno agli altri due. Si suppone che X2 sia interno, esiste pertanto un verso per cui X1 precede X2 ed X2 precede X3, ed il verso opposto per cui X3 precede X2 ed X2 precede X1. Nel primo caso si ha:

Cioè, se X2 è interno ad X1 ed X3, si può asserire che
1) X1X3 = X1X2 + X2X3,
dove tutti sono segmenti orientati.
Quindi la misura del segmento somma è dato dalla somma delle misure dei segmenti.
Si considerano le varie misure dei segmenti della 1), cioè:
X1X3 = αOU, X1X2 = βOU, X2X3 = γOU,
e, sostituendo in essa, si ha
αOU = βOU + γOU,
o anche
2) α = β + γ.
Finora si sono considerati comuni segmenti, ora si considerano segmenti orientati:
per quanto riguarda il verso si sa che sono concordi, quindi si può dire che X1 precede X3 e quindi tutti i segmenti orientati hanno lo stesso verso. Si presentano due casi:
1)-si suppongono tutti e tre concordi, cioè X1X2, X2X3, X1X3 ed OU sono concordi e le varie misure risultano
d13 = α, d12 = β, d23 = γ;
2)-si suppone che i segmenti X1X2, X2X3, X1X3 abbiano il verso opposto a quello di OU, quindi risulta
d13 = -α, d12 = -β, d23 = -γ.
Nel primo caso, se si considera la relazione α = β + γ, si ha:
3) d13 = d12 + d23.
Ricordando la proprietà secondo cui la misura del segmento somma è dato dalla somma delle misure dei segmenti, si suppone che, considerando i punti X1 ed X3 tali che
d13 = -d31,
sostituendo nella relazione 3), si ha:
-d31 = d12 + d23,
o anche
d12 + d23 + d31 = 0.
Nel secondo caso, si moltiplica la relazione α = β + γ per -1, cioè:
-α = -β + (-γ).
Considerando
-α = d13, -β = d12, -γ = d23,
si ha
d13 = d12 + d23.
Si può quindi dire che, comunque si considerino tre punti X1, X2, X3 sulla retta euclidea, e comunque si considerino le misure dei tre segmenti, la seguente relazione sarà sempre soddisfatta:
d12 + d23 + d31 = 0.
Tale relazione è sempre valida, anche quando due dei tre punti coincidono, ossia se
X1 = X3,
d31 = 0
e la relazione suddetta si trasforma in
d12 + d23 = 0.
Invece di d23 si può scrivere sempre d21, poichè
X1 = X3,
quindi
Supponendo di aver dimostrato una relazione con n punti, n ≥ 3, con n intero, si vuol provare che la dimostrazione è analoga anche per n + 1 punti.
Infatti, si suppone di avere sulla retta n punti:
X1, X2, X3, ..., Xn-1, Xn
e di aver dimostrato che
a) d12 + d23 + d34 + ... + d(n-1)n + dn1 = 0,
ricordando che
d(n-1)n
è la misura del segmento
Xn-1Xn
e che
dn1
è la misura del segmento
XnX1.
Si considerino ora n + 1 punti:
X1, X2, X3, ..., Xn-1, Xn, Xn+1
e di essi si prendano i tre punti
X1, Xn, Xn+1,
per i quali vale la proprietà già enunciata per tre punti, quindi si ha
b) d1n + dn(n+1) + d(n+1)1 = 0.
Portando dn1 al secondo membro della a), si ha:
d12 + d23 + ... + d(n-1)n = - dn1 = d1n.
Sostituendo nella b) il valore di d1n, si ha:
d12 + d23 + ... + d(n-1)n + dn(n+1) + d(n+1)1 = 0.
E' stato quindi dimostrato che, se la formula è valida per n punti, è valida anche per n + 1 punti.
Ci si serve ora di tale risultato per determinare la misura dei segmenti orientati, quando si conoscono le ascisse degli estremi dei segmenti orientati.
Si consideri di avere la seguente figura:

Comunque siano disposti X1 ed X2, si conoscono le ascisse x1 ed x2, cioè
X1(x1) ed X2(x2).
Si ricorda il significato di ascissa; essa è la misura del segmento OX1 rispetto ad OU,
x1 = α, se dato OX1 = αOU, X1 appartiene alla semiretta positiva,
x1 = -α, se dato OX1 = αOU, X1 appartiene alla semiretta negativa.
Dire che X1 appartiene alla semiretta positiva equivale a dire che OX1 è concorde con OU, cioè U ed X1 sono sulla stessa semiretta e risulta:

L'ascissa x1 è positiva.
Dire che X1 appartiene alla semiretta negativa equivale a dire che O precede U ed X1 precede O, quindi i due segmenti OU ed OX1 sono discordi e risulta

L'ascissa x1 è negativa.
Si considerano i punti O, X1 ed X2 di ascisse x1 ed x2, applicando la relazione fra i tre punti si ha:

Tale relazione si può scrivere anche

e, sapendo che

si ha
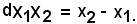
Quindi, la misura del segmento orientato mediante le ascisse è uguale alla differenza dell'ascissa del secondo punto meno l'ascissa del primo punto.
Assegnati due riferimenti simili su una retta, (O, U) ed
(O, U) ed  (O', U'), si vuole determinare la relazione analitica fra le ascisse di uno stesso punto rispetto ad essi.
(O', U'), si vuole determinare la relazione analitica fra le ascisse di uno stesso punto rispetto ad essi.
Allo scopo, siano x l'ascissa del punto X rispetto al primo riferimento ed x' l'ascissa dello stesso punto X rispetto al secondo riferimento.

Si deve trovare la relazione che intercorre fra x ed x'.
Per quanto detto in precedenza, risulta:
x = dOX, rispetto ad (O, U),
(O, U),
x' = dO'X', rispetto ad (O', U').
(O', U').
I due segmenti unitari sono in relazione e quindi si può scrivere
O'U' = βOU,
con β > 0.
Si consideri la misura di O'U' rispetto ad OU, cioè
1) dO'U' = β se O'U' è concorde con OU, dO'U' = -β se O'U' è discorde con OU.
Si consideri inoltre la misura di O'X rispetto ad O'U'; se O'X = αO'U', con α > 0, si ha:
2) dO'X = α se O'X' è concorde con O'U', dO'X = -α se O'X è discorde con O'U'.
Allora, sostituendo nella relazione O'X = αO'U' il valore O'U' = βOU, si ha:
O'X = (αβ)OU.
A tal punto, si considera la misura del segmento orientato O'X rispetto ad OU, e si ha:
3) dO'X = αβ se O'X' è concorde con OU, dO'X = -αβ se O'X è discorde con OU.
Si suppone ora che nella 1) e nella 2) O'U' è concorde con OU ed OU è concorde con O'X; da ciò risulta OU concorde con O'X e quindi la 3) diventa
*) dO'X = αβ = d'O'Xd'O'U'.
Supponendo inoltre che O'U' è concorde con OU ed O'X è discorde da O'U'; da ciò risulta O'X' discorde da OU e quindi la 3) diventa
*) dO'X = -αβ = (-α)β = d'O'Xd'O'U'.
Come può notarsi, le due espressioni contrassegnate da *) rappresentano la stessa relazione
dO'X = d'O'Xd'O'U',
da cui si deduce

D'altronde,
d'O'X = x',
cioè è l'ascissa di O'X rispetto ad OU, e supponendo che d'O'U' = h, h numero reale diverso da zero, dalla 4) si ha:

Si considerino ora O, O' ed X, per questi tre punti vale la relazione precedente, cioè
dOO' + dO'X + dXO = 0,
quindi
dO'X = dOX - dOO',
ricordando che
dOX = x,
è l'ascissa di OX rispetto ad OU e che dOO' è l'ascissa della nuova origine rispetto all'antico riferimento. Si indica
dOO' = x0,
e sostituendo nella relazione 5)
dO'X = dOX - dOO',
si ha:
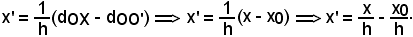
In tale formula

poichè h ≠ 0, mentre

può essere uguale a zero, e ciò si verifica se O' coincide con O.
Ponendo

con β numero a piacere, si ha la relazione fra l'ascissa di un segmento rispetto all'antico riferimento e l'ascissa dello stesso punto rispetto al nuovo riferimento:
x' = αx + β,
cioè x' è uguale ad un polinomio di primo grado in x.
Si osserva quindi che esiste una relazione dei numeri reali nell'insieme dei numeri reali

tale che ad ogni x associ x' e risulti uguale ad αx + β. Ciò determina una corrispondenza biunivoca senza eccezioni: se si fissa un x', esiste un unico x appartenente ad R, tale che
x' = αx + β,
in altri termini
 x'
x' R
R  x
x R
R  x' = αx + β.
x' = αx + β.
Si considera ora
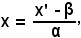
cioè la soluzione dell'equazione suddetta è considerata una trasformazione lineare intera.
Se si ha un riferimento (O, U) e si fissa x' = αx + β, cioè se si considerano un riferimento ed una trasformazione lineare intera
(O, U) e si fissa x' = αx + β, cioè se si considerano un riferimento ed una trasformazione lineare intera

esiste un secondo riferimento (O', U') che è verificato da
(O', U') che è verificato da
x' = αx + β.
Infatti, indicando sempre,

siccome

si può, nel riferimento assegnato, determinare il punto O' della retta r, che ha come ascissa x0, cioè O' tale che
dOO' = x0.
Si considera il punto U' tale che la misura del segmento orientato O'U' sia uguale ad h.
Riassumendo:
O' dOO' = x0, U'
dOO' = x0, U'  dO'U' = h.
dO'U' = h.

I segmenti che sulla retta hanno estremo O' ed hanno misura |h|, h in valore assoluto, sono due e si scelga quello la cui misura del segmento orientato è proprio h. Si assumano questi due punti come fondamentali del nuovo riferimento (O', U'). Si hanno così due riferimenti
(O', U'). Si hanno così due riferimenti  (O, U) ed
(O, U) ed  (O', U') e si determina la trasformazione che dall'ascissa di
(O', U') e si determina la trasformazione che dall'ascissa di  (O, U) permette di passare all'ascissa di
(O, U) permette di passare all'ascissa di  (O', U'); essa ha equazione:
(O', U'); essa ha equazione:

Pertanto, si vede che il nuovo riferimento è tale che il passaggio dalle precedenti alle nuove ascisse ha proprio come equazione quella che si era prefissata. Esiste quindi un riferimento (O',
U'), tale che la trasformazione sia proprio quella prefissata. Ora si
deve dimostrare l'unicità, ossia che tale punto è unico. Allo scopo, si
supponga che esiste un altro riferimento
(O',
U'), tale che la trasformazione sia proprio quella prefissata. Ora si
deve dimostrare l'unicità, ossia che tale punto è unico. Allo scopo, si
supponga che esiste un altro riferimento  (O'', U'') e si considerino
(O'', U'') e si considerino  (O, U) ed
(O, U) ed  (O'', U'), si ha l'equazione
(O'', U'), si ha l'equazione

in cui
h' = dO''U'', x'0 = dOO''.
Se

coincide con

dovrà essere
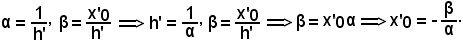
Ricordando che (O', U') era stato costruito in modo tale che x'0 = x0, si ha che la nuova origine O'' coincide con O', perchè le ascisse rispetto ad OU sono uguali, cioè
(O', U') era stato costruito in modo tale che x'0 = x0, si ha che la nuova origine O'' coincide con O', perchè le ascisse rispetto ad OU sono uguali, cioè
U'' dO''U'' = h' = 1/α
dO''U'' = h' = 1/α  h = h'.
h = h'.
Resta così dimostrato che O' = O'' e, dalla precedente relazione, sostituendo O' ad O'', risulta
U'' dO''U'' = dO'U'.
dO''U'' = dO'U'.
Si deduce quindi che U' coincide con U'', pertanto, resta dimostrato che i due riferimenti coincidono, cioè l'unicità del riferimento esistente.
Rapporto semplice di tre punti
Si supponga di aver fissato sulla retta euclidea r un riferimento (O, U) e si consideri una terna ordinata di punti X1 X2 ed X3 con la condizione X2 ≠ X3.
(O, U) e si consideri una terna ordinata di punti X1 X2 ed X3 con la condizione X2 ≠ X3.
Si chiama rapporto semplice della terna ordinata di punti X1, X2 ed X3 il numero reale

essendo x1, x2, x3 ordinatamente le ascisse dei tre punti X1 X2, X3 nel riferimento assegnato.
Il rapporto semplice è un numero reale, perchè X2 ≠ X3, quindi anche il rapporto semplice è diverso da zero.
Tale rapporto semplice si indica come segue:

A tal punto, si può dimostrare che il rapporto semplice è indipendente dal riferimento poichè, se si cambia riferimento, cambiano le ascisse ma il numero ottenuto dal rapporto semplice è sempre lo stesso.
Allo scopo, si considerino un altro riferimento (O', U') ed x' = αx + β, in cui α
(O', U') ed x' = αx + β, in cui α
 , β
, β
 , α ≠ 0.
, α ≠ 0.
Se si indicano con x'1, x'2 ed x'3 le nuove ascisse rispetto al nuovo riferimento, conoscendo le formule di trasformazione, si ha:
x'1 = αx1 + β, x'2 = αx2 + β, x'3 = αx3 + β.
Ora, si consideri il rapporto semplice di questi tre punti:

Come appunto volevasi dimostrare.
D'altronde, il rapporto semplice si può scrivere sotto la seguente forma:
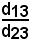
e, considerando un altro segmento unitario, analogamente si ha

Quindi

Punto medio
Si considerino due punti distinti X1 ≠ X2, se X3 è un punto medio tra X1 ed X2, il rapporto semplice della terna ordinata dev'essere uguale a -1:
(X1 X2 X3) = -1.
Biunivocamente, se il rapporto semplice della terna ordinata è uguale a -1, il punto X3 è medio tra X1 ed X2:
(X1 X2 X3) = -1 (X1 ≠ X2)
(X1 ≠ X2)  (X3 punto medio tra X1 ed X2).
(X3 punto medio tra X1 ed X2).
Pertanto, X3 è interno ad X1 ed X2, e ciò equivale a dire che X1 precede X3 ed X3 precede X2 in uno dei versi, in modo che il segmento orientato X1X3 sia concorde ed uguale al segmento X3X2. Si conclude che:
1) (X1 ≠ X2, X3 punto medio tra X1 ed X2) X1X3 = X3X2.
X1X3 = X3X2.
Si considerino ora, in un qualsiasi riferimento (O, U), i segmenti orientati uguali che, rispetto ad esso, hanno uguali misure. Pertanto, dalla relazione 1) segue:
(O, U), i segmenti orientati uguali che, rispetto ad esso, hanno uguali misure. Pertanto, dalla relazione 1) segue:
d13 = d32 = -d23.
Essendo X1 ≠ X2, X3 ≠ X1 X3 ≠ X2, d23 ≠ 0, si può dividere la relazione
X3 ≠ X2, d23 ≠ 0, si può dividere la relazione
d13 = -d23
per la quantità d23, pertanto in ultima analisi:

ma
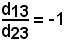
non è altro che il rapporto semplice (X1 X2 X3) della terna, quindi quanto asserito è vero.
Si dimostra ora il viceversa, cioè per ipotesi si suppone che il rapporto semplice (X1 X2 X3) della terna sia uguale a -1, si deve dimostrare che X3 è punto medio tra X1 ed X2.
Infatti, essendo

Considerando sempre la condizione d23 ≠ 0, si ha
d13 = d32 X1X3 = X3X2.
X1X3 = X3X2.
Si deve dimostrare che le misure dei segmenti orientati X1X3 ed X3X2 sono uguali; essi hanno lo stesso verso, cioè X1 precede X3 ed X3 precede X2, cioè
X1 ≠ X2, X2 ≠ X3,
ciò significa che X1 ed X2 sono punti distinti, e ciò comporta anche che X3 è punto interno.
In definitiva si deduce che, essendo i segmenti orientati uguali ed X3 interno, X3 risulta punto medio tra X1 ed X2, quindi è soddisfatta la condizione necessaria e sufficiente affinchè X3 sia punto medio, cioè:
(X1 X2 X3) = -1.
Se si verificasse l'ipotesi X1 = X2, si avrebbe che X1 precede X3 ed X3 precede X1, quindi i tre punti coincidono.
A tal punto si può asserire che:

Si osserva ora che, se i punti X1, X2 ed X3 hanno ascisse x1, x2 ed x3, dall'uguaglianza ora ottenuta si ha:
x3 - x1 = -(x3 - x2),
x3 - x1 = -x3 + x2,
2x3 = x1 + x2,

quindi l'ascissa media risulta uguale alla semisomma delle ascisse estreme, o meglio alla semisomma delle ascisse dei punti assegnati. Tale formula vale anche nel caso in cui si verifichi la coincidenza tra x1 ed x2.
Ciò significa che fra due punti distinti A e B esistono sempre altri punti interni ad essi, pertanto si definisce segmento di estremi A e B l'insieme di tali punti, compresi A e B.
Postulato della continuità o di Dedekind
Si consideri sulla retta euclidea un segmento OP e si supponga di fissare come verso quello quello per cui O precede P. Sia I l'insieme dei punti del segmento OP, esso è suddiviso in due classi:
-la prima classe contiene O,
-la seconda classe contiene P.
Si osserva ora che ogni punto del segmento appartiene ad una sola classe ed ogni punto della prima classe precede ogni punto della seconda classe, cioè esiste un punto A appartenente al segmento OP, ed appartenente ad una sola classe, in modo che ogni punto della seconda classe segue A.
Con ciò si dimostra che, dato un segmento unitario OU, si può costruire un altro segmento OC tale che sia α volte OU, cioè
OC = αOU.
Si consideri una retta r e si fissino su di essa due punti distinti, O ed U, O ≠ U, ed il verso per cui O precede U.
O si chiama origine ed U punto unitario.
E' stato così fissato un riferimento OU, indicato con
Si può quindi affermare che esiste una corrispondenza biunivoca senza eccezioni fra i punti della retta ed i numeri reali, cioè esiste una relazione che associa ad ogni punto della retta uno ed un solo numero reale; viceversa, fissato un numero reale appartenente all'insieme dei numeri reali, esiste uno ed un solo punto della retta r che è associato al numero reale.
Si considerano ora i punti della semiretta che contiene il punto U, supposta positiva, mentre quella che non contiene U è supposta negativa; si prende inoltre un punto X ≠ O, ossia si può considerare il segmento OX ed affermare che esiste uno ed un solo numero reale positivo tale che OX risulta multiplo di OU secondo il numero reale α. Si associa cioè al punto X il numero reale positivo α, tale che sia
OX = αOU.
Se invece X coincide con zero, allora al punto O si associa il numero zero dei numeri reali. Ora si considerano i punti X che appartengono alla semiretta negativa, si prende X ≠ O e si associa al punto X il numero reale negativo -α, per cui sia
OX = -αOU.
Ascissa
Il numero associato ad un punto prende il nome di ascissa, ossia α è ascissa di X e si scrive
X(α),
cioè X di ascissa α. L'ascissa dell'origine è 0 e quella del punto unitario è 1.
Se si cambia il riferimento
Segmenti orientati
Si consideri una retta r e si fissino su di essa due punti distinti, X1 ed X2, X1 ≠ X2, che sono estremi del segmento X1X2:
Si considera la coppia formata dagli estremi X1 ed X2 e dal verso secondo cui X1 precede X2.
La coppia di verso X1X2 si chiama segmento orientato.
Due segmenti orientati sono uguali quando le coppie che formano i segmenti hanno primi e secondi membri uguali, cioè per definizione:
X1X2 = X2X3
Se X1 ed X2 sono due punti ed X1 = X2, X1X2 = X2X1;
Si considerano due segmenti X1X2 ed X3X4, si dice che essi sono concordi, se il verso secondo il quale X1 precede X2 è lo stesso per cui X3 precede X4; se invece il verso è opposto, si dicono discordi.
Misura del segmento orientato
E' noto come si misura un comune segmento, cioè la misura X1X2, rispetto ad OU, è tale che
X1X2 = αOU.
Per i segmenti orientati, si considera sulla retta r il verso secondo cui O precede U, tale che:
se X1X2 è concorde con OU, si chiama misura del segmento orientato il numero α;
se X1X2 è discorde con OU, si chiama misura del segmento orientato il numero -α.
La misura del segmento orientato si chiama anche distanza orientata di X2 da X1.
Osservazione
Si indica la misura del segmento orientato X1X2 con d12 e la misura del segmento orientato X2X1 con d21, d'altronde risultano:
d12 = α, d21 = -α,
quindi
d12 = -d21,
cioè
d12 + d21 = 0.
Si può dire che:
-comunque si prendano sulla retta due punti X1 ed X2, e si comunque si considerino i due segmenti orientati, la somma delle loro misure è uguale a zero.
Si cerca ora di estendere tale relazione: si prendano sulla retta tre punti X1, X2 ed X3, se questi sono distinti, uno ed uno solo è interno agli altri due. Si suppone che X2 sia interno, esiste pertanto un verso per cui X1 precede X2 ed X2 precede X3, ed il verso opposto per cui X3 precede X2 ed X2 precede X1. Nel primo caso si ha:
Cioè, se X2 è interno ad X1 ed X3, si può asserire che
1) X1X3 = X1X2 + X2X3,
dove tutti sono segmenti orientati.
Quindi la misura del segmento somma è dato dalla somma delle misure dei segmenti.
Si considerano le varie misure dei segmenti della 1), cioè:
X1X3 = αOU, X1X2 = βOU, X2X3 = γOU,
e, sostituendo in essa, si ha
αOU = βOU + γOU,
o anche
2) α = β + γ.
Finora si sono considerati comuni segmenti, ora si considerano segmenti orientati:
per quanto riguarda il verso si sa che sono concordi, quindi si può dire che X1 precede X3 e quindi tutti i segmenti orientati hanno lo stesso verso. Si presentano due casi:
1)-si suppongono tutti e tre concordi, cioè X1X2, X2X3, X1X3 ed OU sono concordi e le varie misure risultano
d13 = α, d12 = β, d23 = γ;
2)-si suppone che i segmenti X1X2, X2X3, X1X3 abbiano il verso opposto a quello di OU, quindi risulta
d13 = -α, d12 = -β, d23 = -γ.
Nel primo caso, se si considera la relazione α = β + γ, si ha:
3) d13 = d12 + d23.
Ricordando la proprietà secondo cui la misura del segmento somma è dato dalla somma delle misure dei segmenti, si suppone che, considerando i punti X1 ed X3 tali che
d13 = -d31,
sostituendo nella relazione 3), si ha:
-d31 = d12 + d23,
o anche
d12 + d23 + d31 = 0.
Nel secondo caso, si moltiplica la relazione α = β + γ per -1, cioè:
-α = -β + (-γ).
Considerando
-α = d13, -β = d12, -γ = d23,
si ha
d13 = d12 + d23.
Si può quindi dire che, comunque si considerino tre punti X1, X2, X3 sulla retta euclidea, e comunque si considerino le misure dei tre segmenti, la seguente relazione sarà sempre soddisfatta:
d12 + d23 + d31 = 0.
Tale relazione è sempre valida, anche quando due dei tre punti coincidono, ossia se
X1 = X3,
risulta
d31 = 0
e la relazione suddetta si trasforma in
d12 + d23 = 0.
Invece di d23 si può scrivere sempre d21, poichè
X1 = X3,
quindi
d12 + d21 = 0.
Supponendo di aver dimostrato una relazione con n punti, n ≥ 3, con n intero, si vuol provare che la dimostrazione è analoga anche per n + 1 punti.
Infatti, si suppone di avere sulla retta n punti:
X1, X2, X3, ..., Xn-1, Xn
e di aver dimostrato che
a) d12 + d23 + d34 + ... + d(n-1)n + dn1 = 0,
ricordando che
d(n-1)n
è la misura del segmento
Xn-1Xn
e che
dn1
è la misura del segmento
XnX1.
Si considerino ora n + 1 punti:
X1, X2, X3, ..., Xn-1, Xn, Xn+1
e di essi si prendano i tre punti
X1, Xn, Xn+1,
per i quali vale la proprietà già enunciata per tre punti, quindi si ha
b) d1n + dn(n+1) + d(n+1)1 = 0.
Portando dn1 al secondo membro della a), si ha:
d12 + d23 + ... + d(n-1)n = - dn1 = d1n.
Sostituendo nella b) il valore di d1n, si ha:
d12 + d23 + ... + d(n-1)n + dn(n+1) + d(n+1)1 = 0.
E' stato quindi dimostrato che, se la formula è valida per n punti, è valida anche per n + 1 punti.
Ci si serve ora di tale risultato per determinare la misura dei segmenti orientati, quando si conoscono le ascisse degli estremi dei segmenti orientati.
Si consideri di avere la seguente figura:
Comunque siano disposti X1 ed X2, si conoscono le ascisse x1 ed x2, cioè
X1(x1) ed X2(x2).
Si ricorda il significato di ascissa; essa è la misura del segmento OX1 rispetto ad OU,
x1 = α, se dato OX1 = αOU, X1 appartiene alla semiretta positiva,
x1 = -α, se dato OX1 = αOU, X1 appartiene alla semiretta negativa.
Dire che X1 appartiene alla semiretta positiva equivale a dire che OX1 è concorde con OU, cioè U ed X1 sono sulla stessa semiretta e risulta:
L'ascissa x1 è positiva.
Dire che X1 appartiene alla semiretta negativa equivale a dire che O precede U ed X1 precede O, quindi i due segmenti OU ed OX1 sono discordi e risulta
L'ascissa x1 è negativa.
Si considerano i punti O, X1 ed X2 di ascisse x1 ed x2, applicando la relazione fra i tre punti si ha:
Tale relazione si può scrivere anche
e, sapendo che
si ha
Quindi, la misura del segmento orientato mediante le ascisse è uguale alla differenza dell'ascissa del secondo punto meno l'ascissa del primo punto.
Assegnati due riferimenti simili su una retta,
Allo scopo, siano x l'ascissa del punto X rispetto al primo riferimento ed x' l'ascissa dello stesso punto X rispetto al secondo riferimento.
Si deve trovare la relazione che intercorre fra x ed x'.
Per quanto detto in precedenza, risulta:
x = dOX, rispetto ad
x' = dO'X', rispetto ad
I due segmenti unitari sono in relazione e quindi si può scrivere
O'U' = βOU,
con β > 0.
Si consideri la misura di O'U' rispetto ad OU, cioè
1) dO'U' = β se O'U' è concorde con OU, dO'U' = -β se O'U' è discorde con OU.
Si consideri inoltre la misura di O'X rispetto ad O'U'; se O'X = αO'U', con α > 0, si ha:
2) dO'X = α se O'X' è concorde con O'U', dO'X = -α se O'X è discorde con O'U'.
Allora, sostituendo nella relazione O'X = αO'U' il valore O'U' = βOU, si ha:
O'X = (αβ)OU.
A tal punto, si considera la misura del segmento orientato O'X rispetto ad OU, e si ha:
3) dO'X = αβ se O'X' è concorde con OU, dO'X = -αβ se O'X è discorde con OU.
Si suppone ora che nella 1) e nella 2) O'U' è concorde con OU ed OU è concorde con O'X; da ciò risulta OU concorde con O'X e quindi la 3) diventa
*) dO'X = αβ = d'O'Xd'O'U'.
Supponendo inoltre che O'U' è concorde con OU ed O'X è discorde da O'U'; da ciò risulta O'X' discorde da OU e quindi la 3) diventa
*) dO'X = -αβ = (-α)β = d'O'Xd'O'U'.
Come può notarsi, le due espressioni contrassegnate da *) rappresentano la stessa relazione
dO'X = d'O'Xd'O'U',
da cui si deduce
D'altronde,
d'O'X = x',
cioè è l'ascissa di O'X rispetto ad OU, e supponendo che d'O'U' = h, h numero reale diverso da zero, dalla 4) si ha:
Si considerino ora O, O' ed X, per questi tre punti vale la relazione precedente, cioè
dOO' + dO'X + dXO = 0,
quindi
dO'X = dOX - dOO',
ricordando che
dOX = x,
è l'ascissa di OX rispetto ad OU e che dOO' è l'ascissa della nuova origine rispetto all'antico riferimento. Si indica
dOO' = x0,
e sostituendo nella relazione 5)
dO'X = dOX - dOO',
si ha:
In tale formula
poichè h ≠ 0, mentre
può essere uguale a zero, e ciò si verifica se O' coincide con O.
Ponendo
con β numero a piacere, si ha la relazione fra l'ascissa di un segmento rispetto all'antico riferimento e l'ascissa dello stesso punto rispetto al nuovo riferimento:
x' = αx + β,
cioè x' è uguale ad un polinomio di primo grado in x.
Si osserva quindi che esiste una relazione dei numeri reali nell'insieme dei numeri reali
tale che ad ogni x associ x' e risulti uguale ad αx + β. Ciò determina una corrispondenza biunivoca senza eccezioni: se si fissa un x', esiste un unico x appartenente ad R, tale che
x' = αx + β,
in altri termini
Si considera ora
cioè la soluzione dell'equazione suddetta è considerata una trasformazione lineare intera.
Se si ha un riferimento
esiste un secondo riferimento
x' = αx + β.
Infatti, indicando sempre,
siccome
si può, nel riferimento assegnato, determinare il punto O' della retta r, che ha come ascissa x0, cioè O' tale che
dOO' = x0.
Si considera il punto U' tale che la misura del segmento orientato O'U' sia uguale ad h.
Riassumendo:
O'
I segmenti che sulla retta hanno estremo O' ed hanno misura |h|, h in valore assoluto, sono due e si scelga quello la cui misura del segmento orientato è proprio h. Si assumano questi due punti come fondamentali del nuovo riferimento
Pertanto, si vede che il nuovo riferimento è tale che il passaggio dalle precedenti alle nuove ascisse ha proprio come equazione quella che si era prefissata. Esiste quindi un riferimento
in cui
h' = dO''U'', x'0 = dOO''.
Se
coincide con
dovrà essere
Ricordando che
U''
Resta così dimostrato che O' = O'' e, dalla precedente relazione, sostituendo O' ad O'', risulta
U''
Si deduce quindi che U' coincide con U'', pertanto, resta dimostrato che i due riferimenti coincidono, cioè l'unicità del riferimento esistente.
Rapporto semplice di tre punti
Si supponga di aver fissato sulla retta euclidea r un riferimento
Si chiama rapporto semplice della terna ordinata di punti X1, X2 ed X3 il numero reale
essendo x1, x2, x3 ordinatamente le ascisse dei tre punti X1 X2, X3 nel riferimento assegnato.
Il rapporto semplice è un numero reale, perchè X2 ≠ X3, quindi anche il rapporto semplice è diverso da zero.
Tale rapporto semplice si indica come segue:
A tal punto, si può dimostrare che il rapporto semplice è indipendente dal riferimento poichè, se si cambia riferimento, cambiano le ascisse ma il numero ottenuto dal rapporto semplice è sempre lo stesso.
Allo scopo, si considerino un altro riferimento
Se si indicano con x'1, x'2 ed x'3 le nuove ascisse rispetto al nuovo riferimento, conoscendo le formule di trasformazione, si ha:
x'1 = αx1 + β, x'2 = αx2 + β, x'3 = αx3 + β.
Ora, si consideri il rapporto semplice di questi tre punti:
Come appunto volevasi dimostrare.
D'altronde, il rapporto semplice si può scrivere sotto la seguente forma:
e, considerando un altro segmento unitario, analogamente si ha
Quindi
Punto medio
Si considerino due punti distinti X1 ≠ X2, se X3 è un punto medio tra X1 ed X2, il rapporto semplice della terna ordinata dev'essere uguale a -1:
(X1 X2 X3) = -1.
Biunivocamente, se il rapporto semplice della terna ordinata è uguale a -1, il punto X3 è medio tra X1 ed X2:
(X1 X2 X3) = -1
Pertanto, X3 è interno ad X1 ed X2, e ciò equivale a dire che X1 precede X3 ed X3 precede X2 in uno dei versi, in modo che il segmento orientato X1X3 sia concorde ed uguale al segmento X3X2. Si conclude che:
1) (X1 ≠ X2, X3 punto medio tra X1 ed X2)
Si considerino ora, in un qualsiasi riferimento
d13 = d32 = -d23.
Essendo X1 ≠ X2, X3 ≠ X1
d13 = -d23
per la quantità d23, pertanto in ultima analisi:
ma
non è altro che il rapporto semplice (X1 X2 X3) della terna, quindi quanto asserito è vero.
Si dimostra ora il viceversa, cioè per ipotesi si suppone che il rapporto semplice (X1 X2 X3) della terna sia uguale a -1, si deve dimostrare che X3 è punto medio tra X1 ed X2.
Infatti, essendo
Considerando sempre la condizione d23 ≠ 0, si ha
d13 = d32
Si deve dimostrare che le misure dei segmenti orientati X1X3 ed X3X2 sono uguali; essi hanno lo stesso verso, cioè X1 precede X3 ed X3 precede X2, cioè
X1 ≠ X2, X2 ≠ X3,
ciò significa che X1 ed X2 sono punti distinti, e ciò comporta anche che X3 è punto interno.
In definitiva si deduce che, essendo i segmenti orientati uguali ed X3 interno, X3 risulta punto medio tra X1 ed X2, quindi è soddisfatta la condizione necessaria e sufficiente affinchè X3 sia punto medio, cioè:
(X1 X2 X3) = -1.
Se si verificasse l'ipotesi X1 = X2, si avrebbe che X1 precede X3 ed X3 precede X1, quindi i tre punti coincidono.
A tal punto si può asserire che:
Si osserva ora che, se i punti X1, X2 ed X3 hanno ascisse x1, x2 ed x3, dall'uguaglianza ora ottenuta si ha:
x3 - x1 = -(x3 - x2),
x3 - x1 = -x3 + x2,
2x3 = x1 + x2,
quindi l'ascissa media risulta uguale alla semisomma delle ascisse estreme, o meglio alla semisomma delle ascisse dei punti assegnati. Tale formula vale anche nel caso in cui si verifichi la coincidenza tra x1 ed x2.