MIKY & GENNY
TRIANGOLI ---> INDICE
DEFINIZIONE DI TRIANGOLO
Dicesi triangolo la figura formata da tre segmenti che hanno gli estremi in tre punti non allineati e dalla parte di piano da essi racchiusa.
Per precisare cosa s'intende per parte di piano racchiusa da tre segmenti, che hanno gli estremi in tre punti non allineati, si procede come segue.
Presi tre punti A, B, C, si tracciano le semirette:
-AB ed AC uscenti da A e che passano per gli altri punti B e C, ottenendo l'angolo
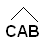
-CA e CB uscenti da C e che passano per gli altri punti A e B, ottenendo l'angolo

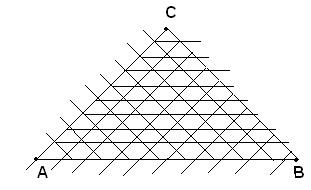
I tre angoli ottenuti hanno in comune una parte di piano che si dice racchiusa dai segmenti AB, BC, CA. Pertanto, per parte di piano racchiusa da tre segmenti aventi gli estremi nei punti A, B, C, non allineati, s'intende la parte di piano comune agli angoli di vertici A, B e C, i cui lati passano per gli altri due punti.
Il triangolo è una figura convessa perchè è una figura comune a tre angoli convessi.
Il triangolo seguente si legge triangolo ABC; i punti A, B e C, si dicono vertici del triangolo; i segmenti AB, BC e CA, lati del triangolo; l'insieme dei lati contorno del triangolo.
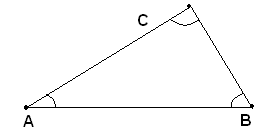
Chiamasi angoli interni di un triangolo, gli angoli che hanno come vertici i vertici del triangolo e per lati le semirette di due lati consecutivi.
Gli angoli del triangolo ABC sono:

L'insieme dei lati e degli angoli si chiamano elementi del triangolo.
Un lato ed un angolo si dicono:
-opposti, quando il vertice dell'angolo non appartiene a quel lato, che equivale a dire che il vertice dell'angolo è fuori dal lato;
-adiacenti, quando il vertice dell'angolo è estremo del lato;
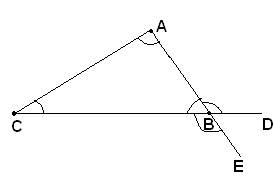
Si chiamano angoli esterni di un triangolo, gli angoli adiacenti agli stessi angoli interni.
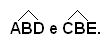
Nel triangolo ABC il lato AB è opposto all'angolo in C, l'angolo in A è opposto al lato BC. Gli angoli in B ed in C sono adiacenti al lato BC. Sono esterni gli angoli
CLASSIFICAZIONE DEI TRIANGOLI
Rispetto ai lati
Un triangolo rispetto ai lati si chiama:
-scaleno, se ha i tre lati disuguali.
-isoscele, se ha due lati uguali. Il lato disuguale si chiama base del triangolo, gli angoli adiacenti ad essa, angoli alla base e l'angolo opposto angolo al vertice.
-equilatero, se ha tutti e tre i lati uguali. Un triangolo equilatero si può considerare isoscele in tre modi diversi, potendosi considerare come base uno qualsiasi dei tre lati.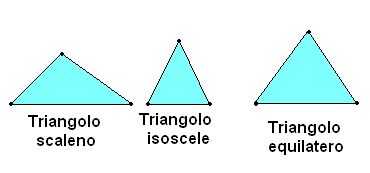
Rispetto agli angoli
Dicesi triangolo la figura formata da tre segmenti che hanno gli estremi in tre punti non allineati e dalla parte di piano da essi racchiusa.
Per precisare cosa s'intende per parte di piano racchiusa da tre segmenti, che hanno gli estremi in tre punti non allineati, si procede come segue.
Presi tre punti A, B, C, si tracciano le semirette:
-AB ed AC uscenti da A e che passano per gli altri punti B e C, ottenendo l'angolo
-BC e BA uscenti da B e che passano per gli altri punti A e B, ottenendo l'angolo
-CA e CB uscenti da C e che passano per gli altri punti A e B, ottenendo l'angolo

I tre angoli ottenuti hanno in comune una parte di piano che si dice racchiusa dai segmenti AB, BC, CA. Pertanto, per parte di piano racchiusa da tre segmenti aventi gli estremi nei punti A, B, C, non allineati, s'intende la parte di piano comune agli angoli di vertici A, B e C, i cui lati passano per gli altri due punti.
Il triangolo è una figura convessa perchè è una figura comune a tre angoli convessi.
Il triangolo seguente si legge triangolo ABC; i punti A, B e C, si dicono vertici del triangolo; i segmenti AB, BC e CA, lati del triangolo; l'insieme dei lati contorno del triangolo.

ANGOLI DI UN TRIANGOLO
Chiamasi angoli interni di un triangolo, gli angoli che hanno come vertici i vertici del triangolo e per lati le semirette di due lati consecutivi.
Gli angoli del triangolo ABC sono:
L'insieme dei lati e degli angoli si chiamano elementi del triangolo.
Un lato ed un angolo si dicono:
-opposti, quando il vertice dell'angolo non appartiene a quel lato, che equivale a dire che il vertice dell'angolo è fuori dal lato;
-adiacenti, quando il vertice dell'angolo è estremo del lato;
Si chiamano angoli esterni di un triangolo, gli angoli adiacenti agli stessi angoli interni.
Nel triangolo ABC il lato AB è opposto all'angolo in C, l'angolo in A è opposto al lato BC. Gli angoli in B ed in C sono adiacenti al lato BC. Sono esterni gli angoli


Rispetto ai lati
Un triangolo rispetto ai lati si chiama:
-scaleno, se ha i tre lati disuguali.
-isoscele, se ha due lati uguali. Il lato disuguale si chiama base del triangolo, gli angoli adiacenti ad essa, angoli alla base e l'angolo opposto angolo al vertice.
-equilatero, se ha tutti e tre i lati uguali. Un triangolo equilatero si può considerare isoscele in tre modi diversi, potendosi considerare come base uno qualsiasi dei tre lati.

Rispetto agli angoli
Un triangolo rispetto agli angoli si chiama:
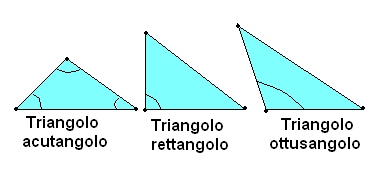
-acutangolo, se ha i tre angoli acuti.
-rettangolo, se ha un angolo retto. I due lati che comprendono l'angolo retto si chiamano cateti, mentre il lato opposto all'angolo retto si chiama ipotenusa.
-ottusangolo, se ha un angolo ottuso.
-acutangolo, se ha i tre angoli acuti.
-rettangolo, se ha un angolo retto. I due lati che comprendono l'angolo retto si chiamano cateti, mentre il lato opposto all'angolo retto si chiama ipotenusa.
-ottusangolo, se ha un angolo ottuso.

CRITERI DI UGUAGLIANZA DEI TRIANGOLI
Per verificare se due triangoli sono uguali o no, secondo la definizione generale di uguaglianza, occorre vedere se è possibile farli coincidere punto per punto. Ora si dimostra che la conoscenza dell'uguaglianza di alcuni lati, non necessariamente tutti, e di alcuni angoli di due triangoli, comporta di conseguenza l'uguaglianza dei triangoli stessi. Si hanno così i seguenti criteri di uguaglianza dei triangoli.
Primo criterio di uguaglianza dei triangoli
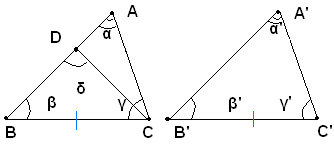
Se due triangoli hanno rispettivamente uguali due lati e l'angolo compreso sono uguali.
Ipotesi: Siano dati due triangoli ABC, A'B'C' e sia AB=A'B', AC=A'C' e α=α'.
Tesi: si vuole dimostrare che i due triangoli sono uguali.
Dimostrazione: Si trasporta il triangolo A'B'C' in modo che l'angolo in A' si sovrapponga all'angolo uguale in A del triangolo ABC e che le semirette A'B' e A'C' si sovrappongano rispettivamente alle semirette AB e AC. Siccome i segmenti AB e A'B' sono uguali, B' coincide con B e pure, essendo per ipotesi A'C'=AC, C' coincide con C. Pertanto i tre vertici ed i tre lati del triangolo A'BC' coincidono rispettivamente con i tre vertici ed i tre lati del triangolo ABC e quindi ogni punto del primo con ogni ogni punto del secondo. Pertanto i due triangoli sono dunque uguali, come dovevasi dimostrare.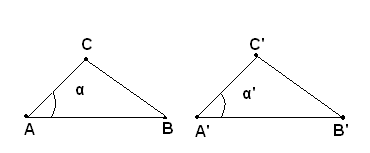
Per verificare se due triangoli sono uguali o no, secondo la definizione generale di uguaglianza, occorre vedere se è possibile farli coincidere punto per punto. Ora si dimostra che la conoscenza dell'uguaglianza di alcuni lati, non necessariamente tutti, e di alcuni angoli di due triangoli, comporta di conseguenza l'uguaglianza dei triangoli stessi. Si hanno così i seguenti criteri di uguaglianza dei triangoli.
Primo criterio di uguaglianza dei triangoli
Se due triangoli hanno rispettivamente uguali due lati e l'angolo compreso sono uguali.
Ipotesi: Siano dati due triangoli ABC, A'B'C' e sia AB=A'B', AC=A'C' e α=α'.
Tesi: si vuole dimostrare che i due triangoli sono uguali.
Dimostrazione: Si trasporta il triangolo A'B'C' in modo che l'angolo in A' si sovrapponga all'angolo uguale in A del triangolo ABC e che le semirette A'B' e A'C' si sovrappongano rispettivamente alle semirette AB e AC. Siccome i segmenti AB e A'B' sono uguali, B' coincide con B e pure, essendo per ipotesi A'C'=AC, C' coincide con C. Pertanto i tre vertici ed i tre lati del triangolo A'BC' coincidono rispettivamente con i tre vertici ed i tre lati del triangolo ABC e quindi ogni punto del primo con ogni ogni punto del secondo. Pertanto i due triangoli sono dunque uguali, come dovevasi dimostrare.

Corollario
In un triangolo isoscele gli angoli alla base sono uguali.
Sia ABC un triangolo isoscele ed AB la sua base. Si vuole dimostrare che l'angolo alla base di vertice A è uguale all'angolo alla base di vertice B.
Infatti, si considera la bisettrice dell'angolo in C. I due triangoli ACD e BCD hanno il lato CD in comune, AC=CB per ipotesi, e gli angoli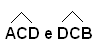
anche uguali per costruzione: segue che i due triangoli sono uguali. Risulta allora che l'angolo in A, opposto a CD, è uguale all'angolo in B, opposto allo stesso CD.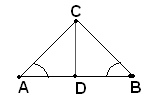
Secondo criterio di uguaglianza dei triangoli
Se due triangoli hanno un lato ed i due angoli adiacenti ad esso rispettivamente uguali, sono uguali.
Ipotesi: Siano dati due triangoli ABC, A'B'C' e sia AB=A'B', α=α', β=β'.
In un triangolo isoscele gli angoli alla base sono uguali.
Sia ABC un triangolo isoscele ed AB la sua base. Si vuole dimostrare che l'angolo alla base di vertice A è uguale all'angolo alla base di vertice B.
Infatti, si considera la bisettrice dell'angolo in C. I due triangoli ACD e BCD hanno il lato CD in comune, AC=CB per ipotesi, e gli angoli

anche uguali per costruzione: segue che i due triangoli sono uguali. Risulta allora che l'angolo in A, opposto a CD, è uguale all'angolo in B, opposto allo stesso CD.

Secondo criterio di uguaglianza dei triangoli
Se due triangoli hanno un lato ed i due angoli adiacenti ad esso rispettivamente uguali, sono uguali.
Ipotesi: Siano dati due triangoli ABC, A'B'C' e sia AB=A'B', α=α', β=β'.
Tesi: si vuole dimostrare che i due triangoli sono uguali.
Dimostrazione: Si trasporta il triangolo A'B'C' in modo che il lato A'B' si sovrapponga al lato AB del triangolo ABC, ad esso uguale per ipotesi, ed in modo che il vertice C' cada dalla stessa parte di C rispetto ad AB. Poichè l'angolo α'=α, e poichè uno dei suoi lati, A'B', coincide con il lato AB dell'angolo α, l'altro lato di A', cioè la semiretta A'C', si sovrappone alla semiretta AC; analogamente, essendo per ipotesi l'angolo β'=β, anche la semiretta B'C' si sovrappone alla semiretta BC. Perciò il punto C', comune alle semirette A'C', e B'C' deve coincidere con il punto C, comune alle due semirette AC e BC. Dunque coincidono i tre vertici e quindi i tre lati, perciò i due triangoli sono uguali, come dovevasi dimostrare.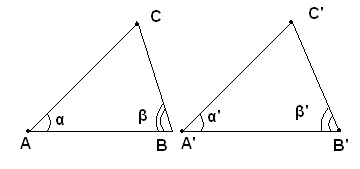
Terzo criterio di uguaglianza dei triangoli
Se due triangoli hanno i tre lati rispettivamente uguali, sono uguali.
Ipotesi: Siano dati due triangoli ABC, A'B'C' e sia AB=A'B'; BC=B'C'; CA=C'A'.
Tesi: si vuole dimostrare che i due triangoli sono uguali.
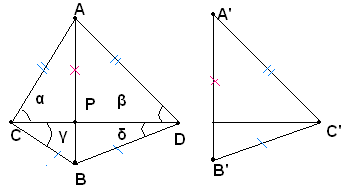
Dimostrazione fase per fase
1)-Si trasporta il triangolo A'B'C' in modo che uno dei suoi lati, ad esempio A'B', si sovrapponga al suo lato uguale AB, e che risulti situato dalla parte opposta del triangolo ABC rispetto alla retta del lato comune AB.
2)-Sia ABD la nuova posizione del triangolo A'B'C', evidentemente risulta AC=AD e, analogamente risulta BC=BD.
3)-I due triangoli ACD e BCD, che si ottengono unendo C con D sono quindi isosceli sulla base CD, e perciò sono uguali gli angoli alla base α e β del primo triangolo, e γ e δ del secondo triangolo.
4)-Supponendo la congiungente CD interna ai due triangoli, tutto l'angolo in C risulta somma degli angoli α e γ, ed è uguale a tutto l'angolo in D, somma degli angoli rispettivamente uguali ai primi β e δ.
5)-Pertanto i due triangoli ABC e ABD, avendo due lati rispettivamente uguali (AC=AD e BC=BD) ed uguale l'angolo fra essi compreso (l'angolo in C avente per lati CA, CB uguale all'angolo in D avente per lati DA, DB), per il primo criterio di uguaglianza dei triangoli, sono uguali.
6)-Siccome il triangolo ABD non è altro che il triangolo A'B'C' spostato, sono quindi uguali i triangoli ABC e A'B'C', come dovevasi dimostrare.
Supponendo che la congiungente CD incontra la retta AB in un punto P esterno al lato AB, i due angoli
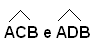
risultano uguali come differenza di angoli uguali.
Supponendo che la congiungente CD incontra il lato AB in uno degli estremi, i due angoli

risultano uguali come angoli alla base di un triangolo isoscele.
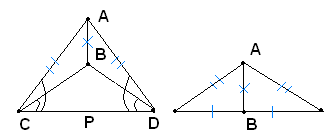
Osservazione
Come conseguenza della definizione generale di uguaglianza delle figure, e come si è visto durante le dimostrazioni precedenti, si ha che:
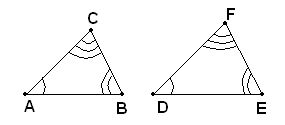
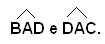
-se due triangoli sono uguali, i lati e gli angoli dell'uno risultano ordinatamente uguali ai lati e agli angoli dell'altro. Precisamente, sono uguali i lati opposti agli angoli rispettivamente uguali, ed evidentemente sono uguali gli angoli opposti ai lati rispettivamente uguali. Così, se nei due triangoli ABC e DEF, si hanno le coppie di angoli uguali
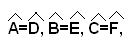
i lati rispettivamente uguali sono BC ed EF, opposti rispettivamente agli angoli uguali in A ed in D; AC e DF, opposti agli angoli uguali in B ed in E; AB e DE opposti agli angoli uguali in C e F.
E viceversa.
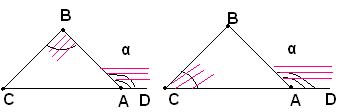
Teorema dell'angolo esterno - In un triangolo, un angolo esterno è maggiore di ciascun angolo interno non adiacente ad esso.Ipotesi: L'angolo α è esterno al triangolo ABC, inoltre l'angolo in B e l'angolo in C sono gli angoli non adiacenti ad esso.
Tesi: si vuole dimostrare che l'angolo α è maggiore sia dell'angolo in B, sia dell'angolo in C.
Dimostrazione: Si considera il punto medio E del lato AB, si congiunge C con E e sul prolungamento di CE si stacca un segmento EF uguale a CE; infine si congiunge F con A.
I due triangoli BEC e EAF sono uguali per il primo criterio, perchè hanno i lati BE ed EA uguali per costruzione, CE ed EF uguali anche per costruzione, ed uguali gli angoli compresi rispettivamente fra i lati uguali, cioè λ e ρ, perchè opposti al vertice.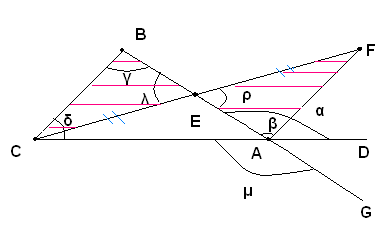
Di conseguenza hanno uguali gli angoli opposti a lati uguali e quindi l'angolo γ opposto al lato CE è uguale all'angolo β opposto al lato EF. Ora l'angolo esterno α è maggiore dell'angolo β che è una sua parte e quindi è anche maggiore dell'angolo uguale γ. Precisamente, risulta: α>γ. Analogamente si dimostra che L'angolo μ, opposto al vertice di α, è maggiore dell'angolo δ; si conclude pertanto che è anche α>δ. Pertanto, il teorema è dimostrato.
Corollario - La somma degli angoli interni di un triangolo è minore di un angolo piatto.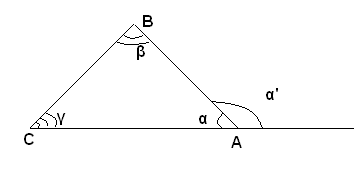
Quarto criterio di uguaglianza dei triangoli
Se due triangoli hanno uguali un lato, un angolo ad esso adiacente ed un angolo opposto, sono uguali.
Ipotesi: I due triangoli ABC, A'B'C' hanno uguali i lati BC e B'C' e gli angoli in B, β, e in , β', a questi adiacenti, ed uguali gli angoli opposti α e α'.
Tesi: si vuole dimostrare che i due triangoli sono uguali.
Dimostrazione: Si sovrappone il triangolo A'BC' al triangolo ABC, in modo che il lato B'C' coincida con BC e l'angolo β' col suo uguale β: il terzo vertice A', dovendo cadere sulla semiretta BA, coincide con A, oppure in un punto qualsiasi della semiretta BA, diverso da A. Quest'ultimo caso non si può verificare: se infatti A' prendesse una posizione D diversa da A, l'angolo α' coinciderebbe con l'angolo δ e quindi sarebbero uguali gli angoli δ ed α in quanto entrambi uguali all'angolo α', e ciò non può essere per il teorema dell'angolo esterno applicato al triangolo ACD, l'angolo δ è esterno e l'angolo α è interno non adiacente. Dovendo quindi A', dopo il movimento considerato, coincidere con A, il triangolo A'B'C' si sovrappone punto per punto al triangolo ABC, ad esso uguale, come dovevasi dimostrare.
Criteri di uguaglianza dei triangoli rettangoli
Per i triangoli rettangoli si hanno quattro criteri di uguaglianza, che possono considerarsi casi particolari di quelli dei triangoli qualsiasi; esiste anche un quinto criterio che sarà dimostrato.
Primo criterio di uguaglianza dei triangoli rettangoli
Se due triangoli rettangoli hanno i cateti rispettivamente uguali, sono uguali.
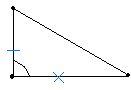

Infatti, essi hanno in comune due lati uguali e l'angolo fra essi compreso, perchè retto; quindi sono uguali per il primo criterio di uguaglianza dei triangoli.
Secondo criterio di uguaglianza dei triangoli rettangoli
Se due triangoli rettangoli hanno uguale un cateto ed un angolo acuto adiacente, sono uguali.

Infatti, i due triangoli hanno in comune un lato uguale e due angoli adiacenti, quello retto e quello acuto per ipotesi. Quindi per il secondo criterio sono uguali.
Terzo criterio di uguaglianza dei triangoli rettangoli
Se due triangoli rettangoli hanno uguale un cateto ed un angolo acuto opposto ad esso, sono uguali.


Infatti, hanno uguale un lato, un angolo adiacente, quello retto, e l'angolo opposto. Quindi per il quarto criterio sono uguali.
Quarto criterio di uguaglianza dei triangoli rettangoli
Se due triangoli rettangoli hanno rispettivamente uguale l'ipotenusa ed un angolo acuto, sono uguali.
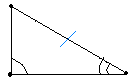

Infatti, hanno uguale un lato, un angolo adiacente ed un angolo opposto, quello retto. Quindi per il quarto criterio sono uguali.
Quinto criterio di uguaglianza dei triangoli rettangoli
Se due triangoli rettangoli hanno uguale l'ipotenusa ed un cateto, sono uguali.
Ipotesi: siano ABC, A'B'C' i due triangoli rettangoli rispettivamente in A e A', che hanno uguali le ipotenuse BC e B'C' ed i cateti AB e A'B'.
Tesi: si vuole dimostrare che i due triangoli sono uguali.
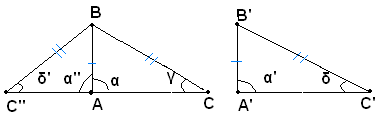
Dimostrazione: si trasporta il triangolo A'B'C' in modo che il cateto A'B' coincida con il suo uguale AB del triangolo ABC e che il vertice C' rimanga dalla parte opposta di C rispetto al lato AB. Sia C'' la nuova posizione del punto C'. Poichè gli angoli α ed α'' sono retti e consecutivi, i lati AC ed AC'' si dispongono su una stessa retta. Pertanto si ottiene il triangolo CBC'' il quale risulta isoscele, essendo per ipotesi BC=BC''. Quindi sono uguali gli angoli alla base γ e δ. I due triangoli rettangoli ABC, ABC'' risultano perciò uguali, perchè hanno uguali le ipotenuse BC e BC'' ed un angolo acuto (γ e in δ'). Siccome il triangolo ABC'' è il triangolo A'B'C' in una diversa posizione, allora segue che i due triangoli ABC ed A'BC' sono uguali, come dovevasi dimostrare.
RELAZIONI FRA ELEMENTI DI TRIANGOLI
Si trattano ora le relazioni di uguaglianza e disuguaglianza fra gli elementi di uno stesso triangolo e poi quelle fra gli elementi di due triangoli differenti.
Uguaglianze fra elementi di uno stesso triangolo
Teorema 1 - Se in un triangolo due lati sono uguali, anche gli angoli ad essi opposti sono uguali. Viceversa, se in un triangolo due angoli opposti sono uguali, anche i lati ad essi opposti sono uguali, cioè il triangolo è isoscele.
Ipotesi: Sia dato il triangolo ABC, con due lati uguali, AB=AC.
Tesi: si vuole dimostrare che gli angoli β e γ, opposti ai lati uguali, sono uguali.
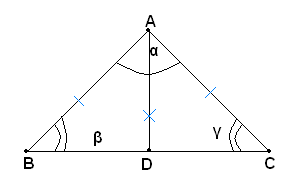
Dimostrazione: essendo AB=AC, il triangolo ABC è isoscele sulla base BC e risultano quindi uguali gli angoli alla base γ e β, che sono opposti ai lati uguali.
Viceversa
Ipotesi: nel triangolo ABC sono uguali gli angoli β e γ.
Tesi: si vuole dimostrare che sono uguali anche i lati AC, AB, rispettivamente opposti ad essi.
Dimostrazione: si traccia la bisettrice AD dell'angolo in A, α. I due triangoli ADB, ADC hanno il lato AD in comune, gli angoli β e γ uguali per ipotesi, ed uguali per costruzione gli angoli
Per il quarto criterio di uguaglianza dei triangoli, i due triangoli sono uguali e quindi risulta AB=CD, come dovevasi dimostrare.
Corollario 1: Un triangolo equilatero è anche equiangolo. Viceversa: Un triangolo equiangolo è anche equilatero.
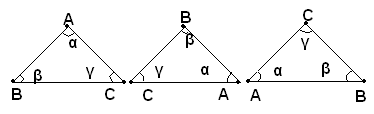
Infatti, un triangolo equilatero ABC può considerarsi isoscele sulla base.
-BC, e quindi gli angoli β e γ sono uguali,
-CA, e quindi gli angoli γ e α sono uguali,-AB, e quindi gli angoli α e β sono uguali.
Quindi segue che α=β=γ. Analogamente si procede nel caso inverso.
Disuguaglianze fra elementi di uno stesso triangolo
Teorema 2 - Se in un triangolo due lati sono disuguali, anche gli angoli ad essi opposti sono disuguali, e precisamente l'angolo opposto al lato maggiore è maggiore dell'angolo opposto al lato minore.
Ipotesi: nel triangolo ABC il lato AC è maggiore del lato AB.
Tesi: si vuole dimostrare che l'angolo β opposto ad AC, è maggiore dell'angolo in C, γ, opposto ad AB.
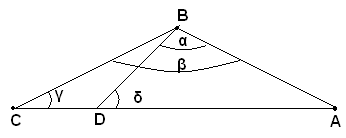
Dimostrazione: sul lato maggiore AC, partendo da A, per ipotesi comune ai due lati disuguali, si stacca un segmento AD=AB. Siccome il punto D è interno al segmento AC, la semiretta BD cade internamente all'angolo β e lo divide in due parti: di conseguenza l'angolo β è maggiore di α. Inoltre il triangolo ABD, per costruzione isoscele sulla base BD, ha gli angoli α e δ uguali, mentre nel triangolo BCD l'angolo esterno δ è maggiore dell'angolo γ interno non adiacente. Quindi si hanno le seguenti relazioni: β>α, α=δ, δ>γ. Dalle prime due relazioni si ricava β>δ, ed essendo δ>γ, a maggior ragione è β>γ. Quindi, l'angolo in B, opposto al lato AC, maggiore di AB, è maggiore dell'angolo in C, opposto ad AB, come volevasi dimostrare.
Teorema 3 - Se in un triangolo due angoli sono disuguali, anche i lati ad essi opposti sono disuguali, e precisamente il lato opposto all'angolo maggiore è maggiore del lato opposto all'angolo minore.
Ipotesi: nel triangolo ABC l'angolo in B, β, è maggiore dell'angolo in C, γ.
Tesi: si vuole dimostrare che il lato AC, opposto all'angolo in B, β, è maggiore del lato AB, opposto all'angolo in C, γ.
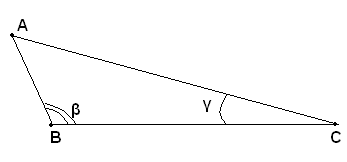
Dimostrazione: infatti il lato AC non può essere uguale al lato AB, perchè in tal caso gli angoli
in B e C, β e γ, sarebbero uguali e ciò non è vero per ipotesi (β>γ); nè può essere il lato AC<AB, perchè l'angolo β, per il teorema precedente, è minore dell'angolo in C, γ, e ciò non è vero per ipotesi. E' quindi vero che che AC>AB.
Corollario 3: in un triangolo rettangolo l'ipotenusa è maggiore di ciascun cateto; in un triangolo ottusangolo il lato opposto all'angolo ottuso è maggiore di ciascuno degli altri due lati.
Infatti, in un triangolo rettangolo l'angolo maggiore è l'angolo retto, e l'ipotenusa è opposta a tale angolo, ed in un triangolo ottusangolo l'angolo maggiore è l'angolo ottuso, poichè gli altri due angoli sono acuti, in entrambi i casi; il lato opposto all'angolo ottuso è perciò maggiore degli altri due lati, che sono opposti agli angoli acuti.
Teorema 4 - In un triangolo ogni lato è maggiore della somma degli altri due.
Ipotesi: sia assegnato il triangolo ABC.
Tesi: si vuole dimostrare che il lato AB è minore della somma degli altri due lati AC e CB.

Dimostrazione: si prolunga il lato AC di un segmento CD uguale a CB e si congiunge D con B. Si ottiene il triangolo isoscele CDB del quale sono uguali gli angoli alla base α e δ. L'angolo α risulta minore di β perchè ne è parte, essendo C tra A e D; segue che anche l'angolo δ, uguale ad α, è minore dell'angolo β. Da ciò si deduce che nel triangolo ABD il lato AB, opposto all'angolo minore δ è minore del lato AD opposto all'angolo maggiore β, cioè AB<AD; ma AD=AC+CD, ovvero, essendo CB=CD, risulta AD= AC+CB; quindi AB<AC+CB.
Teorema 5 - In ogni triangolo un lato è maggiore della differenza degli altri due.
Se il lato AC del triangolo ABC è maggiore di ciascuno degli altri due lati, ovviamente è maggiore della loro differenza, quindi la dimostrazione è immediata. Resta da dimostrare il teorema per ciascuno dei rimanenti lati AB e BC. Si dimostra quindi che il lato AB è maggiore della differenza fra i lati AC e BC.
Infatti, su AC si prende un segmento CD=CB e si congiunge B con D, ottenendo un triangolo isoscele. L'angolo δ, essendo l'angolo alla base di un triangolo isoscele, è acuto, e ciò perchè gli angoli alla base sono uguali e la loro somma dev'essere minore di due angoli retti, quindi l'angolo α adiacente a δ risulta ottuso. Allora nel triangolo ABD il lato AB, opposto all'angolo ottuso, è maggiore del lato AD dello stesso triangolo. Cioè AB>AD. Essendo AD=AC-CD e CD=CB, risulta: AD=AC-CB e quindi AB>AC-CB.
Disuguaglianze fra elementi di triangoli differenti
Teorema 6 - Se due triangoli hanno due lati rispettivamente uguali e l'angolo fra essi compreso disuguale, il terzo lato è maggiore nel triangolo in cui l'angolo opposto è maggiore.
Ipotesi: nei triangoli ABC, A'B'C' si ha: AB=A'B', AC=A'C, λ>μ.
Tesi: si vuole dimostrare che il lato BC>B'C'.
Dimostrazione: infatti, si sposta il triangolo A'B'C' fino a far coincidere il lato A'B' con il lato AB, ad esso uguale per ipotesi, e in modo che esso cada dalla stessa parte di ABC rispetto al lato AB. La nuova posizione del triangolo sia ABC''. Essendo l'angolo μ<λ, il lato A'C' cade internamente all'angolo λ che resta diviso negli angoli α e δ. Di quest'ultimo si traccia la bisettrice e sia D il suo punto d'intersezione con BC. Il triangolo AC''D risulta uguale al triangolo ADC, per il primo criterio, in quanto gli angoli β e γ sono uguali, perchè metà dell'angolo δ, il lato AC è uguale al lato AC'' per ipotesi, e il lato AD è in comune. Quindi è DC''=DC. D'altra parte, se C'' non cade su BC, si ottiene il triangolo BDC'' ed in esso si ha: BC''<BD+DC'', ovvero, essendo DC''=DC, BC''<BD+DC, ed essendo ancora BD+DC=BC, è BC''<BC, ma BC''=B'C', si ha quindi: B'C'<BC, ovvero BC>B'C''. Se il punto C'' cade su BC, si ha senz'altro BC''<BC, e quindi anche B'C'<BC, ovvero BC>A'C'.
Teorema 7 - Se due triangoli hanno due lati rispettivamente uguali ed il terzo lato disuguale, l'angolo compreso fra i due lati uguali è maggiore nel triangolo dove il terzo lato è maggiore.
Ipotesi: nei triangoli ABC, A'B'C' si ha: AB=A'B', AC=A'C', BC>B'C'.
Tesi: si vuole dimostrare che l'angolo in A è maggiore dell'angolo in A', cioè α>α'.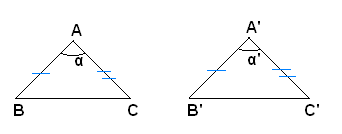
Dimostrazione: infatti, non può essere α=α' poichè per il primo criterio i due triangoli sarebbero uguali e si avrebbe BC=B'C', contro l'ipotesi; non può essere neanche α<α', altrimenti per il teorema precedente si avrebbe BC<B'C', contro l'ipotesi. Dunque α>α'.
ALTEZZA, MEDIANA E BISETTRICE DI UN TRIANGOLO
Altezza di un triangolo
Dicesi altezza di un triangolo, relativa ad un vertice o ad un lato, il segmento di perpendicolare condotto dal vertice alla retta del lato opposto.
Il lato opposto si chiama base del triangolo.
L'altezza di un triangolo relativa ad un lato può essere interna al triangolo, o esterna, o coincidere con uno dei lati.
Precisamente, dato un triangolo ABC:
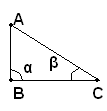
-se uno degli angoli α, β è retto, l'altezza relativa al lato BC coincide o con AB o con AC.
-se uno degli angoli α, β è ottuso, l'altezza relativa al lato BC è esterna al triangolo dalla parte dell'angolo ottuso.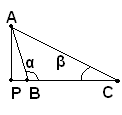
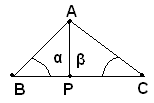
-se gli angoli α, β sono entrambi acuti, l'altezza relativa al lato BC è interna al triangolo.
Infatti, se l'angolo è retto, la perpendicolare condotta da A a BC, essendo unica, deve coincidere con AB (1^ figura).
Se l'angolo α è ottuso (2^ figura), l'altezza AP è esterna al triangolo e dalla parte di B, poichè, qualora fosse interna, il triangolo ABP avrebbe un angolo ottuso e un angolo retto, il che è assurdo.
Se gli angoli α, β sono entrambi acuti, come da figura seguente, l'altezza non può coincidere nè con AB, nè con AC, poichè in questo caso, o, B, o C dovrebbero essere retti: nè può essere esterna, poichè, ad esempio, qualora fosse dalla parte di B, l'angolo esterno α dovrebbe essere acuto e quindi l'angolo interno di vertice A e lati AB e AC, a questo adiacente, dovrebbe essere ottuso, e ciò è contro l'ipotesi.
In ogni triangolo vi sono tre altezze, una per ogni lato che si considera come base.
Mediana di un triangolo
Chiamasi mediana di un triangolo relativa ad un lato il segmento che congiunge il vertice con il punto medio del lato opposto.
Nel triangolo ABC la mediana relativa al lato AB è CM, essendo M il punto medio di AB.
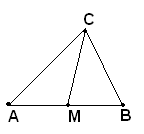
In ogni triangolo vi sono tre mediane, una per ogni lato che si considera come base.
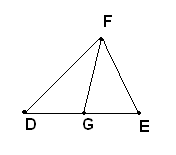
Chiamasi bisettrice di un triangolo il segmento della bisettrice di un angolo dello stesso triangolo compreso fra il vertice e il lato opposto.
Nel triangolo DEF la bisettrice relariva a DE è FG, essendo la semiretta FG la bisettrice dell'angolo in F.
Dimostrazione: Si trasporta il triangolo A'B'C' in modo che il lato A'B' si sovrapponga al lato AB del triangolo ABC, ad esso uguale per ipotesi, ed in modo che il vertice C' cada dalla stessa parte di C rispetto ad AB. Poichè l'angolo α'=α, e poichè uno dei suoi lati, A'B', coincide con il lato AB dell'angolo α, l'altro lato di A', cioè la semiretta A'C', si sovrappone alla semiretta AC; analogamente, essendo per ipotesi l'angolo β'=β, anche la semiretta B'C' si sovrappone alla semiretta BC. Perciò il punto C', comune alle semirette A'C', e B'C' deve coincidere con il punto C, comune alle due semirette AC e BC. Dunque coincidono i tre vertici e quindi i tre lati, perciò i due triangoli sono uguali, come dovevasi dimostrare.

Terzo criterio di uguaglianza dei triangoli
Se due triangoli hanno i tre lati rispettivamente uguali, sono uguali.
Ipotesi: Siano dati due triangoli ABC, A'B'C' e sia AB=A'B'; BC=B'C'; CA=C'A'.
Tesi: si vuole dimostrare che i due triangoli sono uguali.

Dimostrazione fase per fase
1)-Si trasporta il triangolo A'B'C' in modo che uno dei suoi lati, ad esempio A'B', si sovrapponga al suo lato uguale AB, e che risulti situato dalla parte opposta del triangolo ABC rispetto alla retta del lato comune AB.
2)-Sia ABD la nuova posizione del triangolo A'B'C', evidentemente risulta AC=AD e, analogamente risulta BC=BD.
3)-I due triangoli ACD e BCD, che si ottengono unendo C con D sono quindi isosceli sulla base CD, e perciò sono uguali gli angoli alla base α e β del primo triangolo, e γ e δ del secondo triangolo.
4)-Supponendo la congiungente CD interna ai due triangoli, tutto l'angolo in C risulta somma degli angoli α e γ, ed è uguale a tutto l'angolo in D, somma degli angoli rispettivamente uguali ai primi β e δ.
5)-Pertanto i due triangoli ABC e ABD, avendo due lati rispettivamente uguali (AC=AD e BC=BD) ed uguale l'angolo fra essi compreso (l'angolo in C avente per lati CA, CB uguale all'angolo in D avente per lati DA, DB), per il primo criterio di uguaglianza dei triangoli, sono uguali.
6)-Siccome il triangolo ABD non è altro che il triangolo A'B'C' spostato, sono quindi uguali i triangoli ABC e A'B'C', come dovevasi dimostrare.
Supponendo che la congiungente CD incontra la retta AB in un punto P esterno al lato AB, i due angoli
risultano uguali come differenza di angoli uguali.
Supponendo che la congiungente CD incontra il lato AB in uno degli estremi, i due angoli
risultano uguali come angoli alla base di un triangolo isoscele.

Osservazione
Come conseguenza della definizione generale di uguaglianza delle figure, e come si è visto durante le dimostrazioni precedenti, si ha che:
-se due triangoli sono uguali, i lati e gli angoli dell'uno risultano ordinatamente uguali ai lati e agli angoli dell'altro. Precisamente, sono uguali i lati opposti agli angoli rispettivamente uguali, ed evidentemente sono uguali gli angoli opposti ai lati rispettivamente uguali. Così, se nei due triangoli ABC e DEF, si hanno le coppie di angoli uguali
i lati rispettivamente uguali sono BC ed EF, opposti rispettivamente agli angoli uguali in A ed in D; AC e DF, opposti agli angoli uguali in B ed in E; AB e DE opposti agli angoli uguali in C e F.
E viceversa.

Teorema dell'angolo esterno - In un triangolo, un angolo esterno è maggiore di ciascun angolo interno non adiacente ad esso.
Tesi: si vuole dimostrare che l'angolo α è maggiore sia dell'angolo in B, sia dell'angolo in C.

Dimostrazione: Si considera il punto medio E del lato AB, si congiunge C con E e sul prolungamento di CE si stacca un segmento EF uguale a CE; infine si congiunge F con A.
I due triangoli BEC e EAF sono uguali per il primo criterio, perchè hanno i lati BE ed EA uguali per costruzione, CE ed EF uguali anche per costruzione, ed uguali gli angoli compresi rispettivamente fra i lati uguali, cioè λ e ρ, perchè opposti al vertice.

Di conseguenza hanno uguali gli angoli opposti a lati uguali e quindi l'angolo γ opposto al lato CE è uguale all'angolo β opposto al lato EF. Ora l'angolo esterno α è maggiore dell'angolo β che è una sua parte e quindi è anche maggiore dell'angolo uguale γ. Precisamente, risulta: α>γ. Analogamente si dimostra che L'angolo μ, opposto al vertice di α, è maggiore dell'angolo δ; si conclude pertanto che è anche α>δ. Pertanto, il teorema è dimostrato.
Corollario - La somma degli angoli interni di un triangolo è minore di un angolo piatto.
Se α e β sono due angoli di un triangolo, ed α', è l'angolo esterno adiacente ad α, per il teorema precedente si ha β<α' e aggiungendo α ad ambo i membri: α+β<α+α', cioè α+β minore dell'angolo piatto α+α'.

Da
tale corollario si deduce che:
un triangolo non può avere più di un angolo retto o di un angolo ottuso, e se ha un angolo retto o un angolo ottuso, gli altri due sono acuti.
un triangolo non può avere più di un angolo retto o di un angolo ottuso, e se ha un angolo retto o un angolo ottuso, gli altri due sono acuti.
Quarto criterio di uguaglianza dei triangoli
Se due triangoli hanno uguali un lato, un angolo ad esso adiacente ed un angolo opposto, sono uguali.
Ipotesi: I due triangoli ABC, A'B'C' hanno uguali i lati BC e B'C' e gli angoli in B, β, e in , β', a questi adiacenti, ed uguali gli angoli opposti α e α'.
Tesi: si vuole dimostrare che i due triangoli sono uguali.
Dimostrazione: Si sovrappone il triangolo A'BC' al triangolo ABC, in modo che il lato B'C' coincida con BC e l'angolo β' col suo uguale β: il terzo vertice A', dovendo cadere sulla semiretta BA, coincide con A, oppure in un punto qualsiasi della semiretta BA, diverso da A. Quest'ultimo caso non si può verificare: se infatti A' prendesse una posizione D diversa da A, l'angolo α' coinciderebbe con l'angolo δ e quindi sarebbero uguali gli angoli δ ed α in quanto entrambi uguali all'angolo α', e ciò non può essere per il teorema dell'angolo esterno applicato al triangolo ACD, l'angolo δ è esterno e l'angolo α è interno non adiacente. Dovendo quindi A', dopo il movimento considerato, coincidere con A, il triangolo A'B'C' si sovrappone punto per punto al triangolo ABC, ad esso uguale, come dovevasi dimostrare.

Criteri di uguaglianza dei triangoli rettangoli
Per i triangoli rettangoli si hanno quattro criteri di uguaglianza, che possono considerarsi casi particolari di quelli dei triangoli qualsiasi; esiste anche un quinto criterio che sarà dimostrato.
Primo criterio di uguaglianza dei triangoli rettangoli
Se due triangoli rettangoli hanno i cateti rispettivamente uguali, sono uguali.


Infatti, essi hanno in comune due lati uguali e l'angolo fra essi compreso, perchè retto; quindi sono uguali per il primo criterio di uguaglianza dei triangoli.
Secondo criterio di uguaglianza dei triangoli rettangoli
Se due triangoli rettangoli hanno uguale un cateto ed un angolo acuto adiacente, sono uguali.


Infatti, i due triangoli hanno in comune un lato uguale e due angoli adiacenti, quello retto e quello acuto per ipotesi. Quindi per il secondo criterio sono uguali.
Terzo criterio di uguaglianza dei triangoli rettangoli
Se due triangoli rettangoli hanno uguale un cateto ed un angolo acuto opposto ad esso, sono uguali.


Infatti, hanno uguale un lato, un angolo adiacente, quello retto, e l'angolo opposto. Quindi per il quarto criterio sono uguali.
Quarto criterio di uguaglianza dei triangoli rettangoli
Se due triangoli rettangoli hanno rispettivamente uguale l'ipotenusa ed un angolo acuto, sono uguali.


Infatti, hanno uguale un lato, un angolo adiacente ed un angolo opposto, quello retto. Quindi per il quarto criterio sono uguali.
Quinto criterio di uguaglianza dei triangoli rettangoli
Se due triangoli rettangoli hanno uguale l'ipotenusa ed un cateto, sono uguali.
Ipotesi: siano ABC, A'B'C' i due triangoli rettangoli rispettivamente in A e A', che hanno uguali le ipotenuse BC e B'C' ed i cateti AB e A'B'.
Tesi: si vuole dimostrare che i due triangoli sono uguali.

Dimostrazione: si trasporta il triangolo A'B'C' in modo che il cateto A'B' coincida con il suo uguale AB del triangolo ABC e che il vertice C' rimanga dalla parte opposta di C rispetto al lato AB. Sia C'' la nuova posizione del punto C'. Poichè gli angoli α ed α'' sono retti e consecutivi, i lati AC ed AC'' si dispongono su una stessa retta. Pertanto si ottiene il triangolo CBC'' il quale risulta isoscele, essendo per ipotesi BC=BC''. Quindi sono uguali gli angoli alla base γ e δ. I due triangoli rettangoli ABC, ABC'' risultano perciò uguali, perchè hanno uguali le ipotenuse BC e BC'' ed un angolo acuto (γ e in δ'). Siccome il triangolo ABC'' è il triangolo A'B'C' in una diversa posizione, allora segue che i due triangoli ABC ed A'BC' sono uguali, come dovevasi dimostrare.
RELAZIONI FRA ELEMENTI DI TRIANGOLI
Si trattano ora le relazioni di uguaglianza e disuguaglianza fra gli elementi di uno stesso triangolo e poi quelle fra gli elementi di due triangoli differenti.
Uguaglianze fra elementi di uno stesso triangolo
Teorema 1 - Se in un triangolo due lati sono uguali, anche gli angoli ad essi opposti sono uguali. Viceversa, se in un triangolo due angoli opposti sono uguali, anche i lati ad essi opposti sono uguali, cioè il triangolo è isoscele.
Ipotesi: Sia dato il triangolo ABC, con due lati uguali, AB=AC.
Tesi: si vuole dimostrare che gli angoli β e γ, opposti ai lati uguali, sono uguali.

Dimostrazione: essendo AB=AC, il triangolo ABC è isoscele sulla base BC e risultano quindi uguali gli angoli alla base γ e β, che sono opposti ai lati uguali.
Viceversa
Ipotesi: nel triangolo ABC sono uguali gli angoli β e γ.
Tesi: si vuole dimostrare che sono uguali anche i lati AC, AB, rispettivamente opposti ad essi.
Dimostrazione: si traccia la bisettrice AD dell'angolo in A, α. I due triangoli ADB, ADC hanno il lato AD in comune, gli angoli β e γ uguali per ipotesi, ed uguali per costruzione gli angoli
Per il quarto criterio di uguaglianza dei triangoli, i due triangoli sono uguali e quindi risulta AB=CD, come dovevasi dimostrare.
Corollario 1: Un triangolo equilatero è anche equiangolo. Viceversa: Un triangolo equiangolo è anche equilatero.

Infatti, un triangolo equilatero ABC può considerarsi isoscele sulla base.
-BC, e quindi gli angoli β e γ sono uguali,
-CA, e quindi gli angoli γ e α sono uguali,
Quindi segue che α=β=γ. Analogamente si procede nel caso inverso.
Disuguaglianze fra elementi di uno stesso triangolo
Teorema 2 - Se in un triangolo due lati sono disuguali, anche gli angoli ad essi opposti sono disuguali, e precisamente l'angolo opposto al lato maggiore è maggiore dell'angolo opposto al lato minore.
Ipotesi: nel triangolo ABC il lato AC è maggiore del lato AB.
Tesi: si vuole dimostrare che l'angolo β opposto ad AC, è maggiore dell'angolo in C, γ, opposto ad AB.

Dimostrazione: sul lato maggiore AC, partendo da A, per ipotesi comune ai due lati disuguali, si stacca un segmento AD=AB. Siccome il punto D è interno al segmento AC, la semiretta BD cade internamente all'angolo β e lo divide in due parti: di conseguenza l'angolo β è maggiore di α. Inoltre il triangolo ABD, per costruzione isoscele sulla base BD, ha gli angoli α e δ uguali, mentre nel triangolo BCD l'angolo esterno δ è maggiore dell'angolo γ interno non adiacente. Quindi si hanno le seguenti relazioni: β>α, α=δ, δ>γ. Dalle prime due relazioni si ricava β>δ, ed essendo δ>γ, a maggior ragione è β>γ. Quindi, l'angolo in B, opposto al lato AC, maggiore di AB, è maggiore dell'angolo in C, opposto ad AB, come volevasi dimostrare.
Teorema 3 - Se in un triangolo due angoli sono disuguali, anche i lati ad essi opposti sono disuguali, e precisamente il lato opposto all'angolo maggiore è maggiore del lato opposto all'angolo minore.
Ipotesi: nel triangolo ABC l'angolo in B, β, è maggiore dell'angolo in C, γ.
Tesi: si vuole dimostrare che il lato AC, opposto all'angolo in B, β, è maggiore del lato AB, opposto all'angolo in C, γ.

Dimostrazione: infatti il lato AC non può essere uguale al lato AB, perchè in tal caso gli angoli
in B e C, β e γ, sarebbero uguali e ciò non è vero per ipotesi (β>γ); nè può essere il lato AC<AB, perchè l'angolo β, per il teorema precedente, è minore dell'angolo in C, γ, e ciò non è vero per ipotesi. E' quindi vero che che AC>AB.
Corollario 3: in un triangolo rettangolo l'ipotenusa è maggiore di ciascun cateto; in un triangolo ottusangolo il lato opposto all'angolo ottuso è maggiore di ciascuno degli altri due lati.
Infatti, in un triangolo rettangolo l'angolo maggiore è l'angolo retto, e l'ipotenusa è opposta a tale angolo, ed in un triangolo ottusangolo l'angolo maggiore è l'angolo ottuso, poichè gli altri due angoli sono acuti, in entrambi i casi; il lato opposto all'angolo ottuso è perciò maggiore degli altri due lati, che sono opposti agli angoli acuti.
Teorema 4 - In un triangolo ogni lato è maggiore della somma degli altri due.
Ipotesi: sia assegnato il triangolo ABC.
Tesi: si vuole dimostrare che il lato AB è minore della somma degli altri due lati AC e CB.

Dimostrazione: si prolunga il lato AC di un segmento CD uguale a CB e si congiunge D con B. Si ottiene il triangolo isoscele CDB del quale sono uguali gli angoli alla base α e δ. L'angolo α risulta minore di β perchè ne è parte, essendo C tra A e D; segue che anche l'angolo δ, uguale ad α, è minore dell'angolo β. Da ciò si deduce che nel triangolo ABD il lato AB, opposto all'angolo minore δ è minore del lato AD opposto all'angolo maggiore β, cioè AB<AD; ma AD=AC+CD, ovvero, essendo CB=CD, risulta AD= AC+CB; quindi AB<AC+CB.
Teorema 5 - In ogni triangolo un lato è maggiore della differenza degli altri due.
Se il lato AC del triangolo ABC è maggiore di ciascuno degli altri due lati, ovviamente è maggiore della loro differenza, quindi la dimostrazione è immediata. Resta da dimostrare il teorema per ciascuno dei rimanenti lati AB e BC. Si dimostra quindi che il lato AB è maggiore della differenza fra i lati AC e BC.
Infatti, su AC si prende un segmento CD=CB e si congiunge B con D, ottenendo un triangolo isoscele. L'angolo δ, essendo l'angolo alla base di un triangolo isoscele, è acuto, e ciò perchè gli angoli alla base sono uguali e la loro somma dev'essere minore di due angoli retti, quindi l'angolo α adiacente a δ risulta ottuso. Allora nel triangolo ABD il lato AB, opposto all'angolo ottuso, è maggiore del lato AD dello stesso triangolo. Cioè AB>AD. Essendo AD=AC-CD e CD=CB, risulta: AD=AC-CB e quindi AB>AC-CB.

Disuguaglianze fra elementi di triangoli differenti
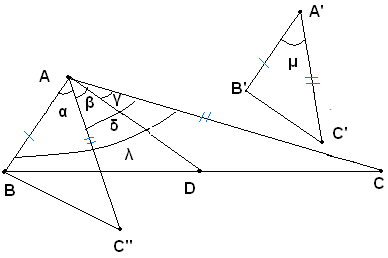
Teorema 6 - Se due triangoli hanno due lati rispettivamente uguali e l'angolo fra essi compreso disuguale, il terzo lato è maggiore nel triangolo in cui l'angolo opposto è maggiore.
Ipotesi: nei triangoli ABC, A'B'C' si ha: AB=A'B', AC=A'C, λ>μ.
Tesi: si vuole dimostrare che il lato BC>B'C'.
Dimostrazione: infatti, si sposta il triangolo A'B'C' fino a far coincidere il lato A'B' con il lato AB, ad esso uguale per ipotesi, e in modo che esso cada dalla stessa parte di ABC rispetto al lato AB. La nuova posizione del triangolo sia ABC''. Essendo l'angolo μ<λ, il lato A'C' cade internamente all'angolo λ che resta diviso negli angoli α e δ. Di quest'ultimo si traccia la bisettrice e sia D il suo punto d'intersezione con BC. Il triangolo AC''D risulta uguale al triangolo ADC, per il primo criterio, in quanto gli angoli β e γ sono uguali, perchè metà dell'angolo δ, il lato AC è uguale al lato AC'' per ipotesi, e il lato AD è in comune. Quindi è DC''=DC. D'altra parte, se C'' non cade su BC, si ottiene il triangolo BDC'' ed in esso si ha: BC''<BD+DC'', ovvero, essendo DC''=DC, BC''<BD+DC, ed essendo ancora BD+DC=BC, è BC''<BC, ma BC''=B'C', si ha quindi: B'C'<BC, ovvero BC>B'C''. Se il punto C'' cade su BC, si ha senz'altro BC''<BC, e quindi anche B'C'<BC, ovvero BC>A'C'.

Teorema 7 - Se due triangoli hanno due lati rispettivamente uguali ed il terzo lato disuguale, l'angolo compreso fra i due lati uguali è maggiore nel triangolo dove il terzo lato è maggiore.
Ipotesi: nei triangoli ABC, A'B'C' si ha: AB=A'B', AC=A'C', BC>B'C'.
Tesi: si vuole dimostrare che l'angolo in A è maggiore dell'angolo in A', cioè α>α'.

Dimostrazione: infatti, non può essere α=α' poichè per il primo criterio i due triangoli sarebbero uguali e si avrebbe BC=B'C', contro l'ipotesi; non può essere neanche α<α', altrimenti per il teorema precedente si avrebbe BC<B'C', contro l'ipotesi. Dunque α>α'.
ALTEZZA, MEDIANA E BISETTRICE DI UN TRIANGOLO
Altezza di un triangolo
Dicesi altezza di un triangolo, relativa ad un vertice o ad un lato, il segmento di perpendicolare condotto dal vertice alla retta del lato opposto.
Il lato opposto si chiama base del triangolo.
L'altezza di un triangolo relativa ad un lato può essere interna al triangolo, o esterna, o coincidere con uno dei lati.
Precisamente, dato un triangolo ABC:
-se uno degli angoli α, β è retto, l'altezza relativa al lato BC coincide o con AB o con AC.

-se uno degli angoli α, β è ottuso, l'altezza relativa al lato BC è esterna al triangolo dalla parte dell'angolo ottuso.

-se gli angoli α, β sono entrambi acuti, l'altezza relativa al lato BC è interna al triangolo.
Infatti, se l'angolo è retto, la perpendicolare condotta da A a BC, essendo unica, deve coincidere con AB (1^ figura).
Se l'angolo α è ottuso (2^ figura), l'altezza AP è esterna al triangolo e dalla parte di B, poichè, qualora fosse interna, il triangolo ABP avrebbe un angolo ottuso e un angolo retto, il che è assurdo.
Se gli angoli α, β sono entrambi acuti, come da figura seguente, l'altezza non può coincidere nè con AB, nè con AC, poichè in questo caso, o, B, o C dovrebbero essere retti: nè può essere esterna, poichè, ad esempio, qualora fosse dalla parte di B, l'angolo esterno α dovrebbe essere acuto e quindi l'angolo interno di vertice A e lati AB e AC, a questo adiacente, dovrebbe essere ottuso, e ciò è contro l'ipotesi.

In ogni triangolo vi sono tre altezze, una per ogni lato che si considera come base.
Mediana di un triangolo
Chiamasi mediana di un triangolo relativa ad un lato il segmento che congiunge il vertice con il punto medio del lato opposto.
Nel triangolo ABC la mediana relativa al lato AB è CM, essendo M il punto medio di AB.

In ogni triangolo vi sono tre mediane, una per ogni lato che si considera come base.
Chiamasi bisettrice di un triangolo il segmento della bisettrice di un angolo dello stesso triangolo compreso fra il vertice e il lato opposto.
Nel triangolo DEF la bisettrice relariva a DE è FG, essendo la semiretta FG la bisettrice dell'angolo in F.

In ogni triangolo vi sono tre bisettrici, una per ogni lato che si considera come base.
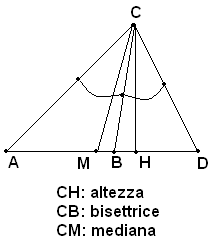
In un triangolo qualsiasi l'altezza, la mediana e la bisettrice relative ad uno stesso lato sono tre segmenti diversi, come può vedersi dalla figura seguente:
Teorema - In un triangolo isoscele la bisettrice, l'altezza e la mediana relative alla base coincidono.
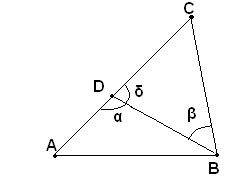
Ipotesi: nel triangolo ABC si consideri la bisettrice CD dell'angolo al vertice C.
Tesi: si vuole dimostrare che CD è anche altezza e mediana.
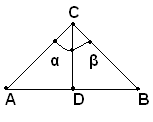
Dimostrazione: infatti i due triangoli ACD e CDB sono uguali per il primo criterio di uguaglianza, perchè hanno il lato CD in comune, i lati AC e CB uguali, e gli angoli α e β anche uguali per costruzione. Pertanto, gli angoli in D con lati rispettivamene DC, DA e DB, DC sono uguali, e poichè sono adiacenti, risultano retti, cioè CD è perpendicolare ad AB: il segmento CD è quindi l'altezza relativa ad AB. Inoltre, sempre dall'uguaglianza degli stessi triangoli, risulta AB=DB, cioè D è il punto medio di AB e CD è la mediana di AB.
Corollario - In un triangolo equilatero la bisettrice, l'altezza e la mediana relative ad un lato qualsiasi coincidono.
Infatti, il triangolo equilatero si può considerare isoscele su qualunque lato considerato come base.
In un triangolo qualsiasi l'altezza, la mediana e la bisettrice relative ad uno stesso lato sono tre segmenti diversi, come può vedersi dalla figura seguente:

Teorema - In un triangolo isoscele la bisettrice, l'altezza e la mediana relative alla base coincidono.
Ipotesi: nel triangolo ABC si consideri la bisettrice CD dell'angolo al vertice C.
Tesi: si vuole dimostrare che CD è anche altezza e mediana.

Dimostrazione: infatti i due triangoli ACD e CDB sono uguali per il primo criterio di uguaglianza, perchè hanno il lato CD in comune, i lati AC e CB uguali, e gli angoli α e β anche uguali per costruzione. Pertanto, gli angoli in D con lati rispettivamene DC, DA e DB, DC sono uguali, e poichè sono adiacenti, risultano retti, cioè CD è perpendicolare ad AB: il segmento CD è quindi l'altezza relativa ad AB. Inoltre, sempre dall'uguaglianza degli stessi triangoli, risulta AB=DB, cioè D è il punto medio di AB e CD è la mediana di AB.
Corollario - In un triangolo equilatero la bisettrice, l'altezza e la mediana relative ad un lato qualsiasi coincidono.
Infatti, il triangolo equilatero si può considerare isoscele su qualunque lato considerato come base.