MIKY & GENNY
FORMULE DI ADDIZIONE E SOTTRAZIONE ---> INDICE
Definizione
- Si chiamano formule di addizione e sottrazione degli angoli, o
degli archi, quelle che esprimono le funzioni goniometriche della somma
e della differenza di due o più angoli, o archi, per mezzo delle
funzioni goniometriche degli angoli, o archi, stessi.
Per ricavare tali formule nel modo più semplice, si segue il procedimento di Cauchy, che si basa sulla formula che esprime la distanza di due punti quando sono note le loro coordinate cioè, considerati i punti P1 (x1, y1) e P2 (x2, y2), la distanza d è data da:
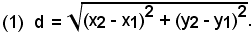
Presi allora due angoli qualunque:
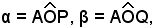
Per ricavare tali formule nel modo più semplice, si segue il procedimento di Cauchy, che si basa sulla formula che esprime la distanza di due punti quando sono note le loro coordinate cioè, considerati i punti P1 (x1, y1) e P2 (x2, y2), la distanza d è data da:
Presi allora due angoli qualunque:
si considera nel cerchio trigonometrico il triangolo isoscele QOP, il cui angolo al vertice ha per misura α - β.
Ricordando la definizione di seno e coseno di un arco come coordinate di un punto della circonferenza goniometrica, si vede che le coordinate dei due estremi P e Q, degli archi
P(cosα, senα), Q(cosβ, senβ)
ed allora per la (1), si ha:
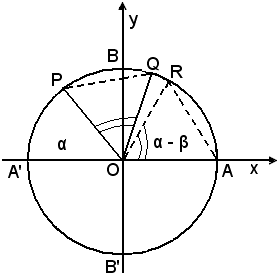
Si costruisce poi sul lato OA il triangolo isoscele AOR uguale al triangolo QOP, quindi risulta
A(1, 0), R[cos(α - β), sen(α - β)],
e quindi, per la (1), si ha
Siccome
Tale uguaglianza si può anche scrivere:
[cos(α - β) - 1]2 + sen2(α - β) = (cosα - cosβ)2 + (senα - senβ)2.
Sviluppando i quadrati, segue:
cos2(α - β) - 2cos(α - β) + 1 + sen2(α - β) = cos2α + cos2β - 2cosαcosβ + sen2α + sen2β
- 2senαsenβ,
da cui, raccogliendo opportunamente i termini,
1 - 2cos(α - β) + [cos2(α - β) + sen2(α - β)] = (cos2α + sen2α) + (cos2β + sen2β) - 2cosαcosβ
- 2senαsenβ,
o anche, ricordando la relazione fondamentaale della goniometria, risulta
1 - 2cos(α - β) + 1 = 1 + 1 - 2cosαcosβ - 2senαsenβ,
e semplificando e cambiando di segno, si ha:
(4) cos(α - β) = cosαcosβ + senαsenβ.
Se nella (4) si sostituisce -β a β, si ha:
cos[α - (-β)] = cosαcos(-β) + senαsen(-β),
da cui, ricordando che angoli opposti hanno coseni uguali e seni opposti, risulta
(4') cos(α + β) = cosαcosβ - senαsenβ.
Se nella (4) si sostituisce 90° - α ad α, si ha:
cos[90° - (α + β)] = cosα(90° - α)cosβ + sen(90° - α)senβ,
e poichè il seno di un angolo è uguale al coseno dell'angolo complementare e viceversa, si ha:
(5) sen(α + β) = senαcosβ + cosαsenβ.
Infine, se in quest'ultima formula si sostituisce -β a β, si ha:
(5) sen(α - β) = senαcosβ - cosαsenβ.
Queste formule esprimono il seno e il coseno degli angoli α + β e α - β in funzione del seno e del coseno degli angoli α e β, quindi sono le formule di addizione e sottrazione degli archi, relative alle funzioni seno e coseno.
Per ottenere le formule della tangente e della cotangente di α + β e α - β, si procede come segue:
allora, dividendo numeratore e denominatore dell'ultima frazione per il prodotto cosαcosβ, supposto diverso da zero, si ha:
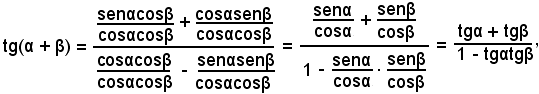
quindi
inoltre, se nella (6) si sostituisce -β a β, e ricordando che tg(-β) = -tgβ, si ha:
Per la cotangente, analogamente si ha:
da cui, dividendo numeratore e denominatore per il prodotto senαsenβ ≠ 0, risulta
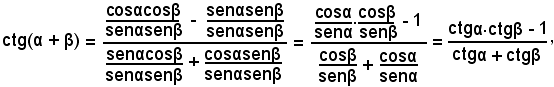
quindi
inoltre, se nella (7) si sostituisce -β a β, si ha:
Per le formule di addizione e sottrazione degli archi, relative alla tangente e alla cotangente, si possono ottenere due espressioni, che però si usano di rado e che quindi ci si limita ad accennare. Ricordando che la cotangente e la tangente di un angolo sono reciproche, si ha:
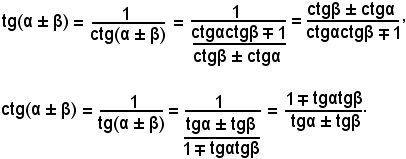
Si stabiliscono anche formule analoghe per le funzioni secante e cosecante:
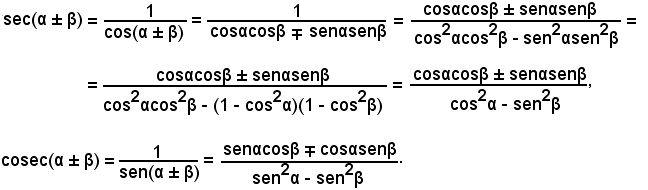
Esempio - Calcolare i valori delle funzioni goniometriche degli angoli di 15° e di 75°.
Evidentemente risulta:
15° = 45° - 30°, 75° = 45° + 30°
applicando le formule stabilite in precedenza, si trova:

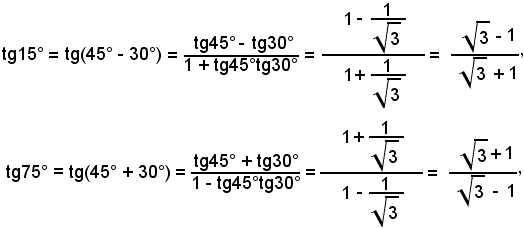
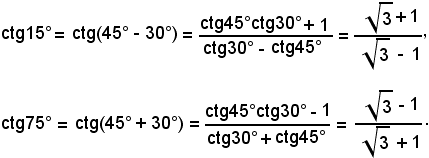
Si verifica subito che:
sen15° = cos75°, cos15° = sen75°, tg15° = ctg75°, ctg15° = tg75°.
Ciò è ovvio, in quanto gli angoli di 15° e 75° sono complementari.
Analogamente si calcolano i valori delle funzioni degli angoli di 12° = 30° - 18° e di 48° = 30° + 18°.