MIKY & GENNY
FORMULE FONDAMENTALI DEI TRIANGOLI ---> INDICE
Elementi di un triangolo
Sia ABC un triangolo qualsiasi, generalmente con le lettere minuscole a, b, c si indicano le lunghezze dei lati opposti ai vertici A, B, C e con α, β, γ l'ampiezza degli angoli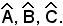
Definizione - Si chiama trigonometria l'insieme delle regole e delle formule che permettono di determinare il valore di alcuni elementi di un triangolo dato, conoscendo gli altri.
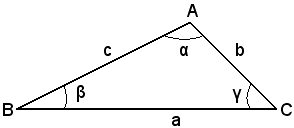
Sia ABC un triangolo qualsiasi, generalmente con le lettere minuscole a, b, c si indicano le lunghezze dei lati opposti ai vertici A, B, C e con α, β, γ l'ampiezza degli angoli
Definizione - Si chiama trigonometria l'insieme delle regole e delle formule che permettono di determinare il valore di alcuni elementi di un triangolo dato, conoscendo gli altri.

Per rendersi conto del significato di tale definizione, si fanno alcune considerazioni sui criteri di uguaglianza dei triangoli; un triangolo è completamente individuato in tre casi:
1)-se si conoscono i tre lati,
2)-se si conoscono un lato e gli angoli adiacenti,
3)-se si conoscono due lati e l'angolo compreso.
Ciò significa che, se due triangoli hanno uguali i tre lati, risultano uguali fra loro, cioè sovrapponibili, e di conseguenza in essi sono individuate le misure degli angoli.
In altri termini, si può affermare che le misure degli angoli risultano funzioni di quelle dei lati. La trigonometria ha lo scopo di determinare tali funzioni, cioè di determinare quelle espressioni che permettono di calcolare le ampiezze dei tre angoli, conoscendo le misure dei lati. I procedimenti che permettono di determinare le misure degli elementi incogniti di un dato triangolo costituiscono la risoluzione di un triangolo. Di conseguenza, in base ai tre criteri di uguaglianza dei triangoli, si può affermare che esisteranno altrettanti casi di risoluzione, cioè:
1° caso
-risoluzione di un triangolo qualsiasi, conoscendo i tre lati;
2° caso
-risoluzione di un triangolo qualsiasi, conoscendo un lato e i due angoli ad esso adiacenti;
3° caso
-risoluzione di un triangolo qualsiasi, conoscendo due lati e l'angolo compreso:
Nota bene
Per esattezza si dovrebbe dire "risoluzione di un triangolo qualsiasi del quale si conoscono le misure dei tre lati", oppure "risoluzione di un triangolo qualsiasi, conoscendo le misure di due lati e l'ampiezza dell'angolo compreso". Per brevità, si omettono i termini "misura" e "ampiezza".
In trigonometria si studia un altro caso di risoluzione, e precisamente il
4° caso
-risoluzione di un triangolo qualsiasi, conoscendo due lati e l'angolo opposto a uno di essi.
Tale caso non dovrebbe essere aggregato ai precedenti, perchè la conoscenza di due lati e dell'angolo opposto ad uno di essi non individua sempre uno ed un solo triangolo. In altri termini, in geometria non esiste un quarto criterio di uguaglianza dei triangoli dal quale si possa far discendere un 4° caso di risoluzione, cioè non esiste un criterio di uguaglianza che affermi "due triangoli sono uguali se hanno due lati uguali e l'angolo opposto ad uno di essi".
Però in pratica è conveniente considerare anche questo caso di risoluzione, che in sostanza, come si vedrà, differisce dagli altri perchè, mentre negli altri casi, soddisfatte eventualmente alcune limitazioni (*) che devono essere verificate dai dati, esiste sempre uno ed un solo triangolo che risolve il problema. Nel caso specifico i dati non individuano un solo triangolo.
Nota bene
(*) Se, ad esempio, si vuole risolvere un triangolo conoscendo i lati a, b, c, questi devono soddisfare la limitazione:
a - b < c < a + b.
Si suppone ora di voler costruire geometricamente un triangolo ABC, conoscendo due lati a, b e l'angolo α, opposto ad uno di essi.
Si traccia un angolo
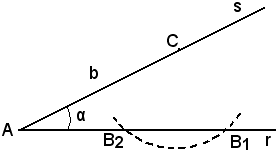
Appena effettuate le risoluzioni dei triangoli nei quattro casi considerati, se si suppone che uno degli angoli sia retto, si ottiene, come caso particolare, la risoluzione dei triangoli rettangoli. Però in pratica, per ragioni pratiche, è preferibile trattare direttamente la risoluzione dei triangoli rettangoli, prima di quella dei triangoli qualsiasi.
Nel caso dei triangoli rettangoli si hanno i seguenti casi di risoluzione, che rientrano come casi particolari, nei quattro casi generali precedentemente descritti.
1° caso
-risoluzione di un triangolo rettangolo, conoscendo i due cateti.
Si tratta di un caso particolare del precedente 3° caso dei triangoli qualsiasi;
2° caso
-risoluzione di un triangolo rettangolo, conoscendo un cateto e l'ipotenusa.
Si tratta di un caso particolare del precedente 4° caso dei triangoli qualsiasi. Si deve però osservare che, conoscendo l'ipotenusa e un cateto, il triangolo rettangolo risulta completamente individuato, perchè per i triangoli rettangoli esiste un particolare criterio di uguaglianza che afferma "due triangoli rettangoli sono uguali se hanno uguali un cateto e l'ipotenusa";
3° caso
-risoluzione di un triangolo rettangolo, conoscendo un cateto e un angolo.
Si tratta di un caso particolare del precedente 2° caso dei triangoli qualsiasi, perchè la conoscenza di un angolo acuto di un triangolo rettangolo comporta anche quella dell'altro;
4° caso
-risoluzione di un triangolo rettangolo, conoscendo un cateto e un angolo.
Si tratta di un caso particolare del precedente 2° caso dei triangoli qualsiasi.
Per trattare la risoluzione dei triangoli, occorre prima stabilire alcuni risultati relativi ai triangoli rettangoli e ai triangoli qualsiasi; si vedrà in seguito.
Relazioni fra gli elementi di un triangolo rettangolo
Sia ABC un triangolo rettangolo in A; la circonferenza di centro C e raggio CB, cioè avente come raggio l'ipotenusa del triangolo, incontra il prolungamento del cateto CA in un punto H.
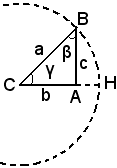
Assumendo la circonferenza come circonferenza goniometrica, per definizione di seno e coseno, si ha:
da cui, dividendo membro a membro, risulta
Riducendo a forma intera, si ottengono le relazioni
(1) c = asenγ, b = acosγ, c = btgγ, b = cctgγ,
dalle quali, dopo avere osservato che c indica il cateto opposto all'angolo γ e b il cateto ad esso adiacente, si deducono due regole fondamentali.
Regola fondamentale I - In un triangolo rettangolo un cateto è uguale all'ipotenusa per il seno dell'angolo opposto, oppure per il coseno dell'angolo adiacente.
Regola fondamentale II - In un triangolo rettangolo un cateto è uguale all'altro per la tangente dell'angolo opposto, oppure per la cotangente dell'angolo adiacente.
Nota bene
Più esattamente si dovrebbe dire "misura di un cateto" e "misura dell'ipotenusa".
Relazioni fra gli elementi di un triangolo qualsiasi
1)-Teorema dei seni - In un triangolo qualsiasi i lati sono proporzionali ai seni degli angoli opposti.
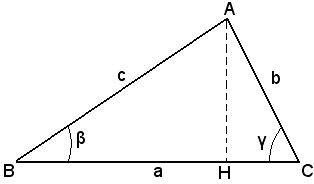
Sia ABC un triangolo qualsiasi e si conduca da una dei vertici la perpendicolare al lato opposto, cioè l'altezza. Se gli angoli adiacenti a tale lato sono entrambi acuti, l'altezza lo interseca in un punto (fig. A), altrimenti interseca il suo prolungamento dalla parte adiacente all'angolo ottuso (fig. B).
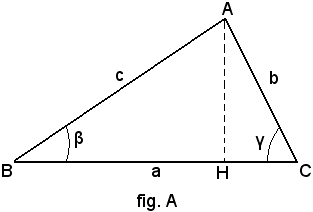
Si suppone prima che il piede dell'altezza AH cada internamente a BC. Il triangolo dato viene diviso nei triangoli rettangoli ABH, ACH, e allora, applicando a ciascuno di essi la regola fondamentale I, si ha:
da cui, uguagliando i secondi membri, risulta
Dividendo entrambi i membri per il prodotto senβsenγ, che è senz'altro diverso da zero, segue
e semplificando
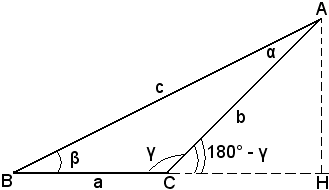
Si suppone ora che il piede H dell'altezza cada sul prolungamento del lato BC.
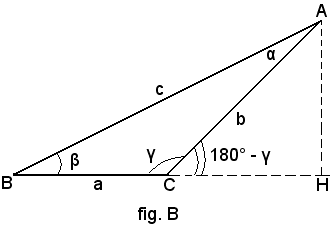
Il triangolo viene diviso nei triangoli rettangoli ABH, ACH, e allora, applicando a ciascuno di essi la regola fondamentale I, si ha:
quindi
bsenγ = csenβ,
da cui
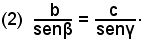
da cui
Poichè tale relazione vale quale che siano gli angoli, se invece di partire dal vertice A, in cui s'incontrano a e b, si parte dal vertice B, comune ai lati a e c, si ottiene la relazione:
che per la proprietà transitiva, permette di scrivere
Il teorema dei seni, afferma in sostanza che in un triangolo qualsiasi è costante il rapporto fra un lato e il seno dell'angolo opposto; ora si vuol calcolare il valore di tale rapporto.
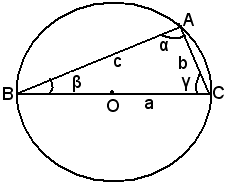
Proprietà - In un triangolo qualsiasi il rapporto costante fra un lato e il seno dell'angolo opposto è uguale al diametro del cerchio ad esso circoscritto.
Infatti, si considera la circonferenza circoscritta al triangolo ABC, avente centro in O e raggio R; il diametro OA incontra ulteriormente la circonferenza in D.
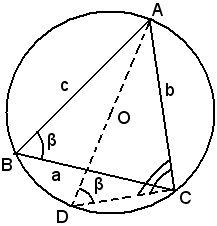
Congiungendo D con uno degli altri vertici, ad esempio C, si ottiene il triangolo ADC, rettangolo in C, perchè l'angolo
Quindi, applicando al triangolo rettangolo ADC la regola fondamentale I, si ha:
o anche
b = 2Rsenβ,
quindi
Nota bene
Nel caso in cui il triangolo sia rettangolo, α = 90° e quindi sen90° = 1, il risultato (3) precedente diventa
da cui
b = a senβ, c = asenγ,
inoltre
a = 2R.
2)-Teorema delle proiezioni - In un triangolo qualsiasi un lato è uguale alla somma dei prodotti di ciascuno degli altri due per il coseno dell'angolo che essi formano rispettivamente con il primo lato.
Dal vertice A di un triangolo qualsiasi ABC si conduce la perpendicolare al lato opposto BC e, analogamente a quanto si è fatto l'altezza cada internamente o esternamente al lato BC.
Nel primo caso, per la regola fondamentale I, si può scrivere:
da cui, sommando membro a membro, e osservando che
risulta
(4) a = bcosγ + ccosβ.
Se invece il piede dell'altezza cade sul prolungamento del lato BC, dai due triangoli rettangoli ABH, ACH, si deduce:
da cui, sottraendo membro a membro ed osservando che in tal caso
risulta
a = bcosγ + ccosβ,
cioè di nuovo la (4).
Si conclude quindi che per qualsiasi triangolo sussiste la relazione
(4) a = bcosγ + ccosβ,
osservando che β, γ sono adiacenti al lato a.
Nota bene
Questo teorema si può dimostrare seguendo un'altra via, che, pur essendo più prolissa della precedente, ha il vantaggio di non distinguere i due casi.
Dalla relazione
α + β + γ = 180°,
si ha:
β + γ = 180° - α
e, considerando i seni sei due membri, risulta
sen(β + γ) = sen(180° - α).
Applicando al primo membro la fomula di addizione, segue:
(*) senβcosγ + cosβsenγ = senα;
ma per il teorema dei seni risulta anche
da cui
Sostituendo queste espressioni nella (*), risulta
Dividendo per senα, senz'altro diverso da zero, e liberando dal denominatore, si ha la (4).
La
(4) vale naturalmente per qualsiasi lato considerato, quindi si
può dire che il teorema delle proiezioni dà luogo alle
seguenti tre relazioni:
(5) a = bcosγ + ccosβ, b = ccosα + acosγ, c = acosβ + bcosα.
3)-Teorema di Carnot o del coseno - In un triangolo qualsiasi un lato al quadrato è uguale alla somma dei quadrati degli altri due, diminuita del doppio prodotto di tali lati per il coseno dell'angolo che essi formano.
Infatti, moltiplicando la prima delle (5) per a, la seconda per b e la terza per c, si ha:
dalle quali, sottraendo dalla prima le altre due, dopo semplici calcoli, si ottiene
e quindi
(6) a2= b2 + c2 - 2bccosα.
Scambiando in tale formula a con b, oppure con c, e di conseguenza α con β oppure con γ, si deducono le tre relazioni:
(7) a2 = b2 + c2 - 2bccosα, b2 = c2 + a2 - 2cacosβ, c2 = a2 + b2 - 2abcosγ.
Tali formule esprimono il teorema di Carnot.
Nota bene
Dopo aver scritto la prima delle (5), le altre due si ottengono con una sostituzione circolare delle lettere a, b, c, e α, β, γ. Ciò significa che a ciascuna lettera dei due gruppi va sostituita la successuva e all'ultima la prima. La stessa circostanza si presenta per le (6) e, come si vedrà, per le formule che esprimono altri teoremi.
Teorema di Carnot o teorema generalizzato di Pitagora
Se nell'espressione (6) α = 90°, e quindi cos90° = 0, si ha:
a2 = b2 + c2,
che esprime il teorema di Pitagora; per questo motivo, il teorema di Carnot si chiama anche teorema generalizzato dI Pitagora.
Il teorema di Carnot traduce in forma algebrica i seguenti teoremi sull'equivalenza:
-in un triangolo qualsiasi il quadrato costruito su un lato, opposto ad un angolo acuto, o ottuso, è equivalente alla somma dei quadrati costruiti sugli altri due lati, diminuita, o aumentata del doppio del rettangolo avente per dimensioni uno di essi e la proiezione dell'altro lato su quello.
Infatti, nel triangolo ABC, si indica con m la proiezione AH del lato AB sul lato AC, come nelle figure seguenti, a seconda che l'angolo α sia acuto o ottuso.
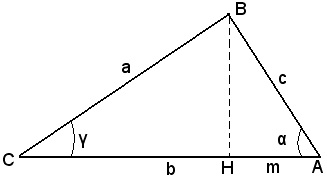
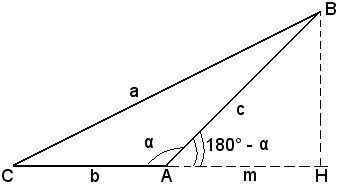
Il teorema precedente si puo esprimere con una delle seguenti relazioni:
o anche, passando alle misure,
A seconda che l'angolo sia acuto o ottuso, però si ha:
quindi, sostituendo segue in ogni caso
a2 = b2 + c2 - 2bccosα.
4)-Formule di Briggs
Le formule (7) del teorema di Carnot:
a2 = b2 + c2 - 2bccosα, b2 = c2 + a2 - 2cacosβ, c2 = a2 + b2 - 2abcosγ
si possono usare per calcolare gli angoli di un triangolo, qualora si conoscano i lati.
Infatti, risolvendo rispetto al coseno, si ottiene
Ma le formule (8) non sono idonee al calcolo logarotmico e quindi in pratica conviene vedere se è possibile sostituirle con altre. Lo scopo si raggiunge facilmente servendosi di bisezione degli archi.
Infatti, se nelle formule di bisezione
si sostuisce al posto di cosα l'espressione data dalla prima delle (8), si ottiene:
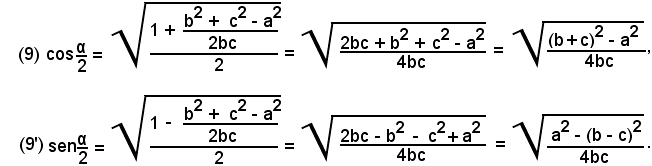
Nota bene
Siccome α è un angolo del triangolo considerato, si ha 0 < α < 180°, e quindi 0 < (α/2) < 90°, il che dimostra che seno e coseno sono positivi.
Si osserva ora che gli ultimi radicali della (9) e della (9') contengono la differenza di due quadrati, che trasformata nel prodotto della somma per la differenza delle basi, permette di scrivere:
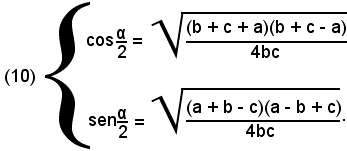
S'introduce ora il perimetro del triangolo dato, che si indica con 2p, cioè si pone:
a + b + c = 2p
e, sottraendo da ambo i membri in successione 2a, 2b, 2c, si ha:
a + b + c - 2a = 2p - 2a, cioè b + c - a = 2(p - a),
a + b + c - 2b = 2p - 2b, cioè a + c - b = 2(p - b),
a + b + c - 2c = 2p - c, cioè a + b - c = 2(p - c).
Sostituendo queste espressioni nelle (10) segue
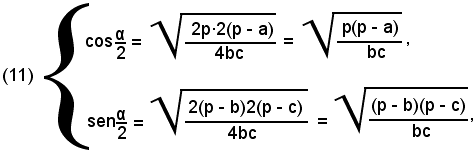
da cui anche, dividendo membro a membro:
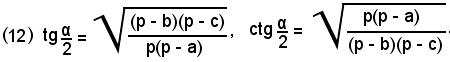
Le (11), le (12) e le analoghe che si potrebbero scrivere effettuando una sostituzione circolare sulle lettere a, b, c e α, β, γ, si chiamano formule di Briggs; esse permettono di trovare gli angoli di un triangolo, quando si conoscono i lati, mediante formule atte al calcolo logaritmico.
Si riportano ora le formule delle tangenti, che saranno applicate in seguito:
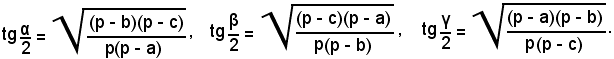
4)-Formule di Nepero
Si parte dalle formule del teorema dei seni, scritte sotto forma di proporzione
e, applicando il componendo e lo scomponendo alla prima proporzione, si ha:
(a + b) : (senα + senβ) = a : senα,
(a - b) : (senα - senβ) = a : senα,
e quindi essendo uguali i secondi membri della due uguaglianze, risulta
(a + b) : (senα + senβ) = (a - b) : (senα - senβ),
oppure
Applicando le formule di prostaferesi, segue:
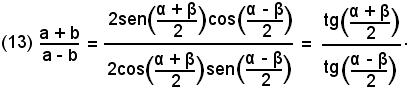
Scambiando le lettere, si scrivono le formule analoghe:
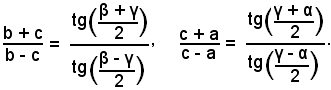
La formule (14) e le analoghe, si chiamano formule di Nepero; il risultato ottenuto si può enunciare come segue:
-in un triangolo qualsiasi la somma di due lati sta alla loro differenza, come la tangente della semisomma degli angoli opposti sta alla tangente della loro semidifferenza.
Le formule di Nepero si possono trasformare convenientemente, tenendo conto che gli angoli α, β, γ di un triangolo sono legati dalla relazione α + α + γ =180°, da cui
α + β = 180° - γ,
o anche
Sostituendo nella (13), si ha:
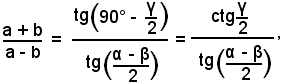
e infine la formula
e le analoghe.
Si considerano ancora le formule del teorema dei seni
si ha pure
Sommando e sottraendo membro a membro le due relazioni suddette, risulta:
o anche, trasformando mediante le formule di prostaferesi, risulta
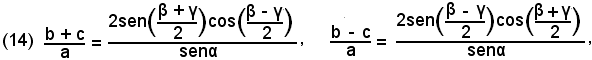
per la formula di duplicazione segue
mentre, essendo β + γ = 180° - α, si ha:
e quindi
Sostituendo questi risultati nelle (14), si ottiene:
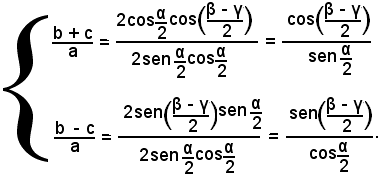
Queste formule, e le analoghe che si potrebbero scrivere permutando le lettere, si chiamano formule di Delambre.
Note storiche
1)-Briggs Enrico, detto l'Archimede inglese, nacque presso Alifax, nella contea di New York, nel 1556 e morì ad Oxford nel 1631; egli pubblicò le prime tavole logaritmiche numeriche in base dieci, perchè più pratiche di quelle in base e, pubblicate da Nepero, e quelle logaritmo-trigonometriche di 10 secondi in 10 secondi quest'ultime completate in seguito dall'astronomo Gunter, nato nel 1580 e morto nel 1626.
2)-Carnot Lazzaro nacque a Nolay in Borgogna nel 1753 e morì a Magdeburgo nel 1823; egli fu un autorevole membro della Convenzione durante la rivoluzione francese e durante l'epopea napoleonica fu messo in disparte. Scrisse importanti opere di geometria proiettiva come "La géometrie de position" e "L'essai des théories des transversales". Nella matematica elementare è ricordato per il teorema intitolato "Teorema di Carnot", che traduce sotto forma analitico-trigonometrica, un ben noto teorema di Euclide sull'equivalenza. Non si confonda Lazzaro Carnot con Nicola Sadi Carnot, nato nel 1796 e morto nel 1832, capitano del Genio, al quale si deve il "Ciclo di Carnot", fondamento della moderna termodinamica.
3)-Delambre Giuseppe nacque ad Amiens nel 1749 e morì a Parigi nel 1822; egli pubblicò nel 1809 le formule analoghe a quelle trattate, relative ad un triangolo sferico. Le formule sopra riportate furono pubblicate un anno prima dal matematico tedesco Mollweide, nato nel 1774 e morto nel 1825. Per tale motivo i tedeschi, più giustamente, le chiamano formule di Mollweide.