Didattica dell’algebra con Cabri-géomètre
Roberto Ricci
Liceo Scientifico "A.Righi"- Bologna
R.S.D.D.M, Dipartimento di Matematica, Università di Bologna.
Summary. In this paper, the author presents some reflections about applications of SW for dynamic geometry in order to visualize elementary algebra. He proposes, moreover, some activities for students aged 14-15: to costruct real numbers, to reduce operations and other formulas to simple constructions, to compose those constructions, to dynamically observe relations between independ and depend variable real points. Through experiences and handlings of points and operations on the real axes, we hope to give a more significant knowledge of algebric formalism.
le motivazioni
Da alcuni anni si assiste a un rinnovato interesse per la ricerca in didattica dell’algebra. Tra le recenti manifestazioni nazionali di rilievo che hanno consentito di fare il punto su queste ricerche si possono ricordare il Seminario Nazionale di Didattica della matematica (Pisa, ’92) e, per un primo tentativo di promuovere una larga ricaduta didattica, il corso UMI-MPI su "Didattica dell’Algebra" (Viareggio, ’94).
In questo scritto l’autore, insegnante nel triennio di un liceo scientifico, particolarmente interessato a quelle applicazioni informatiche alla didattica che creano situazioni di esperienza matematica adatte a rivederne e approfondirne concetti e processi elementari, descrive alcuni materiali per insegnare e apprendere algebra nel biennio della scuola secondaria superiore.
Tra i problemi più comuni, individuati anche nella letteratura, alla cui soluzione si presume possano contribuire tali materiali, si possono citare: la difficoltà di servirsi delle lettere e di farne uso strutturale; il successivo adeguamento a un formalismo algebrico privo di valore semantico, quindi fine a se stesso in particolare nei procedimenti di calcolo; la convinzione che ogni regola di trasformazione algebrica sia lineare e quindi che qualunque manipolazione algebrica lineare sia valida; la difficoltà nel riconoscere e dominare la quantificazione, in particolare nelle dimostrazioni.
Il SW Cabri-géomètre ha fornito la base sulla quale realizzare uno strumento per interpretare l’algebra e produrre un "campo di esperienze" per sviluppare: la padronanza dei significati delle quattro operazioni da cui far emergere le loro proprietà strutturali; una visualizzazione geometrica di numero reale che superi le rappresentazioni numerico-decimali; l’operatività su lettere liberata dalla necessità aritmetizzante di attribuire loro un significato numerico; il concetto di variabile come numero non determinato (lettera a cui associare o sostituire contemporaneamente numeri entro un ambito di valori possibili) e incognita (lettera che rappresenta un sottoinsieme di numeri, da scoprire, entro un ambito di valori possibili); le distinzioni tra variabile e parametro, tra variabile indipendente e dipendente; la capacità di vedere sostituiti alle variabili di una formula più numeri simultaneamente; l’idea di processo di calcolo come costruzione-funzione oltre la pratica del calcolo aritmetico; la capacità di vedere in un’espressione algebrica sia una struttura statica sia un ente operativo-dinamico; la capacità di "vedere" la continuità e la discontinuità di funzioni algebriche.
Più in particolare le esperienze di visualizzazione concreta qui proposte potranno favorire la capacità di manipolazione semantica delle formule algebriche, scomponendo prima il testo sulla base degli operatori e delle funzioni rese disponibili, poi ricomponendo tali costruzioni parziali in un’unica funzione; potranno prevenire errori tipici come ' - x è negativo ', oppure come ' x² > 0 Þ x > 0 '; potranno aiutare a operare correttamente con funzioni come la radice quadrata o il valore assoluto e a risolvere visivamente (dis)equazioni algebriche sulla retta reale; potranno favorire una chiara distinzione tra argomento e valore di una funzione.
Occorre infine avvertire che questo genere di attività è probabilmente inadeguato sia a migliorare la rapidità nella manipolazione simbolica sia ad affrontare argomenti per i quali l’aspetto sintattico è ancor più rilevante, richiedendo una sorta di creatività sintattica come per esempio in teoria dei numeri dove non di rado è determinante saper scegliere opportunamente i nomi da attribuire alle variabili.
gli strumenti
L’idea centrale è dunque realizzare un ambiente visivo entro cui poter svolgere attività di manipolazione algebrica. Con il SW Cabri è sembrato naturale costruire la retta reale e le operazioni sui punti reali. Presa innanzitutto una retta, fissati su quella un punto O che faremo corrispondere al numero 0 e un altro punto U che faremo corrispondere a 1, è possibile concepire una corrispondenza biunivoca tra i punti della retta e i numeri reali, primi "mostri inafferrabili" con cui si ha a che fare in matematica. Tale corrispondenza naturale si ottiene, in parole povere, facendo corrispondere ad ogni punto P il numero reale che esprime, preso OU come unità di misura, la lunghezza di OP se OÏ UP, altrimenti l'opposto della lunghezza di OP.
Chiamata dunque retta numerica reale (r,0,1) l'ente costituito dalla retta r e dai punti "base" 0 e 1, può essere necessario costruire la corrispondenza biunivoca tra tali enti: se (r,0,1) e (r’,0’,1’) sono due rette reali e P è un punto della prima, costruire sulla seconda un punto P’ corrispondente allo stesso numero reale a cui corrisponde, sulla retta reale (r,0,1), il punto P. Se r º r’ e 0 º 0’ si può seguire una costruzione come quella dell’omotetia descritta più avanti per il prodotto tra due numeri reali; se invece r ¹ r’ e 0 º 0’, costruita per P la parallela p alla retta per 1 e 1’, allora P’º pÇ r’; altrimenti, costruita per 0’ la retta s parallela a r, costruiti i punti V e Q di s che corrispondono a 1 e P nella traslazione che porta 0 in 0’, costruire il punto P’ come corrispondente del punto Q della retta reale (s,0’,V), essendosi ricondotti a uno dei casi precedenti.
I punti della retta sono divenuti così una interpretazione dei numeri reali che, grazie alle caratteristiche dell’ambiente Cabri, li fa apparire più "maneggevoli", "afferrabili" e "manipolabili", più di quanto non sia per la rappresentazione abituale in forma decimale; infatti fissare un punto su una retta sembra un'azione mentale banale rispetto a rappresentare un numero reale attraverso una successione illimitata non periodica di cifre decimali, ancor più banale delle rappresentazioni mediante intervalli di approssimazione, sezioni di Dedekind, successioni di Cauchy o altro. Ovviamente la sfuggevolezza dei numeri reali è una caratteristica intrinseca che nessuna possibile interpretazione può evitare: neanche fissare un punto su una retta è un atto del pensiero banale così come può sembrare. Un punto geometrico è infatti un ente astratto, privo di dimensioni, afferrabile concettualmente ma non fisicamente, diverso dal segno lasciato su un foglio dalla punta di una matita quanto dal pixel del video di un PC o dal punto realizzato col menu Creazione dell'ambiente Cabri. Un punto è inoltre circondato da un insieme denso e, ancor più, continuo di altri oggetti identici; ciò che non accade in qualunque raffigurazione fisica come quella nell'ambiente Cabri, che si basa per giunta su un insieme discreto.
Dopo essersi resi conto che i punti idealmente costruibili con Cabri sono infiniti, decisamente troppi per la nostra scarsa sensibilità visiva, ci si potrà rendere conto anche dell’esistenza di punti reali non costruibili a partire dai punti 0 e 1 e mediante l’uso di sola riga e compasso; tuttavia ciò che potrebbe esser considerato quindi una limitazione nell’approccio ai reali con Cabri, consente bene di richiamare anche il problema dell’esistenza di numeri (trascendenti) che, per quanto concepibili con altri procedimenti di calcolo, non sono "costruibili" mediante l’uso di sole operazioni algebriche; perciò dobbiamo accettare di porci di fronte ai numeri reali consapevoli comunque dell’ignoranza che ci deriva da un alfabeto mentale finito e ci impedisce di superare il limite del numerabile; per di più possiamo sfiorarli, questi limiti, constatando che esistono numeri reali definibili, come il numero casuale W introdotto da Chaitin, ma non calcolabili ( si veda ad es. [Gardner, 1980] ).
Consapevoli dei limiti della rappresentazione con Cabri si può passare a realizzare costruzioni che interpretano sulla retta reale le operazioni di addizione e moltiplicazione sui numeri reali, arricchendo la retta di una struttura algebrica isomorfa a quella dei reali. Si esaminano di seguito le costruzioni fondamentali.
Presi due punti X e Y sulla retta reale (r,0,1), il punto X+Y si può ottenere semplicemente osservando che, poiché 2X è simmetrico di 0 rispetto a X, allora X+Y è simmetrico di 0 rispetto alla media aritmetica (X+Y)/2, punto medio del segmento di estremi X e Y. Con Cabri si realizza la costruzione una volta per tutte registrandola come macro-costruzione, così apparirà tra le opzioni del menu Costruzione; in seguito basterà selezionarla, indicare la retta numerica, cioè la retta r e i punti 0 e 1, indicare poi su questa i punti X e Y: verrà costruito così, automaticamente, il punto somma X+Y.
Creare la retta r (
Creazione/Retta)Indicare con r la retta appena creata (
Edizione/Nomi)Costruire il punto 0 su r (
Costruzione/Punto su un oggetto)Indicare con 0 il punto appena costruito (
Edizione/Nomi)Costruire il punto 1 su r (
Costruzione/Punto su un oggetto)Indicare con 1 il punto appena costruito (
Edizione/Nomi)Costruire il punto X su r (
Costruzione/Punto su un oggetto)Indicare con X il punto appena costruito (
Edizione/Nomi)Costruire il punto Y su r (
Costruzione/Punto su un oggetto)Indicare con Y il punto appena costruito (
Edizione/Nomi)Costruire il punto medio M tra X e Y (
Costruzione/Punto medio)Costruire simmetrico di 0 rispetto a M (
Costruzione/Simmetrico di un punto)Indicare con X+Y il punto appena costruito (
Edizione/Nomi)Registrare la macrocostruzione
(
Macrocostruzioni/Nuova/selezionare nell'ordine: retta r, punti 0,1,X e Y / fine degli oggetti iniziali / selezionare il punto X+Y / fine degli oggetti finali / nominare X+Y la macro / registrare un messaggio di aiuto come: "Indicare in questa successione: una retta, i punti 0, 1, X e Y su quella. Il punto costruito è somma di X e Y" / salvare su disco la macro / scegliere ad esempio la directory MACRO e digitare il nome SOMMA)
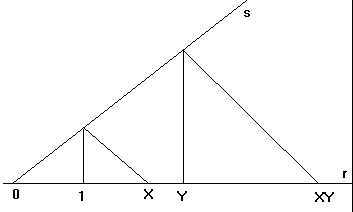
Presi due punti X e Y sulla retta reale (r,0,1), il punto prodotto XY si potrà ottenere con una costruzione geometrica come la seguente:

Costruire la retta reale (r,0,1), il punto X e il punto Y (come per l'addizione)
Costruire la retta perpendicolare da 0 a r (
Costruzione/Retta perpendicolare)Creare la circonferenza di centro 0 passante per 1 (
Creazione/Circonf.(centro / punto))Costruire le intersezioni tra le ultime due curve (
Costruzione / Intersezione di 2 oggetti)Costruire una retta s per 0 diversa da r (
Costruzione / Bisettrice / indicare nell'ordine i punti 0,1 e una delle intersezioni costruite nel passo precedente )Costruire la retta perpendicolare da 1 a r ( Costruzione/Retta perpendicolare)
Costruire punto intersezione tra quest'ultima retta ed s ( Costruzione/Intersezione di 2 oggetti)
Creare il segmento di estremi in X e in quest'ultimo punto (Creazione/ Segmento)
Costruire la perpendicolare da Y ad r(Costruzione/Retta perpendicolare)
Costruire intersezione tra quest'ultima retta ed s ( Costruzione/Intersezione di 2 oggetti)
Costruire per quest'ultimo punto la retta parallela al segmento creato di estremo in X (Costruzione /Retta parallela)
Costruire punto intersezione tra quest'ultima retta ed r (Costruzione/Intersezione di 2 oggetti)
Indicare con XY il punto appena costruito (Edizione / Nomi)
Registrare la macrocostruzione
(Macrocostruzioni / Nuova / selezionare nell'ordine: retta r, punti 0,1,X e Y / fine degli oggetti iniziali / selezionare il punto XY / fine degli oggetti finali / nominare XY la macro / registrare un messaggio di aiuto come: "Indicare in questa successione: una retta, i punti 0, 1, X e Y su quella. Il punto costruito è prodotto di X e Y" / salvare su disco la macro / scegliere ad esempio la directory MACRO e digitare il nome PRODOTTO).
Possiamo osservare in particolare che queste costruzioni sono quelle essenziali. Infatti applicando la macro X+Y ai punti b, 1, 0 e a, nell’ordine, si ottiene il punto a - b, mentre applicando la macro XY ai punti 0, b, 1 e a, nell’ordine, si ottiene il punto a/b.
Una macrocostruzione X2 per il quadrato di un punto reale è tecnicamente indispensabile dal momento che Cabri non consente di indicare due volte lo stesso punto come oggetto iniziale della macro XY.
Costruire la retta reale (r,0,1), il punto X ( come per l'addizione )
Costruire la retta perpendicolare da 0 a r (
Costruzione/Retta perpendicolare)Creare la circonferenza di centro 0 passante per 1 (
Creazione/ Circonf.(centro/ punto) )Costruire le intersezioni tra le ultime due curve (
Costruzione/Intersezione di 2 oggetti )Costruire una retta s per 0 diversa da r (
Costruzione/Bisettrice/ indicare nell'ordine i punti 0,1 e una delle intersezioni costruite nel passo precedente)Costruire la retta perpendicolare da 1 a r ( Costruzione/Retta perpendicolare)
Costruire punto intersezione tra quest'ultima retta ed s ( Costruzione/Intersezione di 2 oggetti )
Creare il segmento di estremi in X e in quest'ultimo punto ( Creazione/ Segmento)
Costruire la retta perpendicolare da X ad r(Costruzione/Retta perpendicolare)
Costruire punto intersezione tra quest'ultima retta ed s (Costruzione/Intersezione di 2 oggetti )
Costruire per quest'ultimo punto la retta parallela al segmento creato di estremo in X (Costruzione /Retta parallela)
Costruire punto intersezione tra quest'ultima retta ed r (Costruzione/Intersezione di 2 oggetti )
Indicare con X2 il punto appena costruito ( Edizione / Nomi)
Registrare la macrocostruzione
(Macrocostruzioni/Nuova/selezionare nell'ordine: retta r, punti 0,1 e X / fine degli oggetti iniziali/selezionare il punto X2 / fine degli oggetti finali/nominare X2 la macro / registrare un messaggio di aiuto come: "Indicare in questa successione: una retta, i punti 0, 1 e X su quella. Il punto costruito è il quadrato di X "/ salvare su disco la macro / scegliere ad esempio la directory MACRO e digitare il nome QUADRATO).
È interessante osservare che la macro X2 può essere applicata anche prendendo nell’ordine 0, x e x2 come punti iniziali e allora si ottiene il punto x3, e così via; oppure può essere applicata prendendo 0, x e 1 come punti iniziali e allora si ottiene il punto 1/x ; oppure prendendo 0, 1/x e 1/x2 come punti iniziali e allora si ottiene il punto 1/x3; e così via.
Si giunge così, in concreto, a un particolare ambiente Cabri arricchito dalle macrocostruzioni che realizzano le operazioni tra i punti reali e che può anche essere predisposto automaticamente, in modo che le operazioni compaiano sin dall’inizio della sessione di lavoro. Ciò è possibile lanciando Cabri tramite un file batch ( .BAT) alternativo a GEOM.BAT che richiami a sua volta un file di sessione ( .SES) alternativo a GEOM.SES nel quale sia riportato l’elenco dei file di macro ( .MAC), oltre all’eventuale file menu ( .MNU), che l’insegnante ritiene opportuni.
Interpretando i numeri reali attraverso i punti di una retta e le operazioni in modo costruttivo, prima concretamente attraverso Cabri e poi idealmente, la nostra intuizione è favorita su molte questioni algebriche che altrimenti, viste in ambito esclusivamente sintattico, rischiano di ridursi sovente, come già detto, a esercizio mnemonico di abilità puramente formali e perciò spesso prive del necessario controllo.
Nell’uso di Cabri come strumento per fare algebra si riscontrano ovviamente anche alcune difficoltà: ad esempio per i calcoli un po’ più complessi, come quello delle radici di un polinomio di II grado, i punti parziali necessari si infittiscono molto, tanto da richiedere particolare attenzione, ordine e pazienza nei passaggi e, anche se d’altra parte ciò può essere utile palestra per sviluppare la concentrazione, non si confà con i limitati tempi scolastici.
le attività
Si può pensare di iniziare subito a svolgere attività nell’ambiente appositamente preparato per l’algebra dei reali: analizzare le proprietà formali delle operazioni, affrontare le attività algebriche descritte più sotto. Non si ritiene indispensabile, per quanto utile, far precedere tali attività dall’esecuzione delle costruzioni per somma e prodotto prima su carta con riga e compasso, poi in ambiente Cabri dove, dopo averne esaminato dinamicamente le proprietà, realizzare anche le altre macro notevoli: X- Y (applicando ad esempio la macro X+Y ai punti Y, 1, X e 0 nell’ordine ), X/Y (applicando ad esempio la macro XY ai punti 0, Y, 1 e X nell’ordine ), X2, 1/X (applicando ad esempio la macro X2 ai punti 0, X e 1 nell’ordine), Ö X .
Visualizzare numeri reali Può essere utile, in un primo tempo, costruire sulla retta reale numeri interi, ad esempio tra - 10 e 10, solo mediante simmetrie ( n è simmetrico di n- 2 rispetto a n- 1, - n è simmetrico di - n+2 rispetto al punto - n+1), alcuni numeri frazionari applicando le macro 1/X oppure X/Y a punti interi, poi le radici quadrate degli interi positivi; eventualmente si possono inoltre costruire punti approssimazioni di p realizzando costruzioni classiche come quella dovuta al gesuita polacco del XVII sec. Adam Kochansky, affetta da un errore di circa 0.00006 unità e quindi più che valida per Cabri.
Anche l’opzione Misura segmento del menu Diversi può essere usata per ritrovare, sia pure con larghe approssimazioni, l’ambiente numerico abituale.
Visualizzare formule di base Si tratta di attività che intendono spingere a collegare formule a semplici costruzioni geometriche come punto medio, simmetrie centrali, omotetie.
Creare il punto x e costruire il punto 4x solo mediante simmetrie.
Costruire il simmetrico di un punto B rispetto al punto medio tra 0 e A. Che espressione algebrica si può associare a quel punto ?
Mostrare che il simmetrico di A rispetto a B è 2B- A ( Ad es.: costruire 2B come simmetrico di 0 rispetto a B; costruire - A come simmetrico di A rispetto a 0; applicare la macro X+Y ai punti 2B e - A; dare nome 2B- A al punto così ottenuto; costruire il simmetrico di A rispetto a B; dare nome A’ al punto così ottenuto dopo aver constatato che Cabri rileva l’ambiguità tra i due punti A’ e 2B- A; variare A e osservare che i due punti A’ e 2B- A restano sovrapposti; variare B e osservare che i due punti A’ e 2B- A restano sovrapposti. Oppure, ad es.: sapendo che (X+Y)/2 è il punto medio tra X e Y, dimostrare col calcolo che B è punto medio tra A e 2B-A) .
Applicare la macro X2 ai punti iniziali 0, a, x e constatare che si ottiene il punto x× a2 che corrisponde ad x nell’omotetia di fattore a2.
Costruire il punto medio M tra A e B, costruire A+C e B+C e convincersi che il punto medio tra questi ultimi è M+C; constatare anche che MC è il punto medio tra AC e BC. Il punto medio tra A2 e B2 è M2 ?
Mostrare che A- B è simmetrico di B rispetto a A/2 , ed è simmetrico di A+B rispetto ad A.
Che formula ha il simmetrico di A rispetto ad A+B ?
Dimostrare con punto medio e simmetrie che A+B/2 = (2A+B)/2.
Posto p = a+b e q = a- b, mostrare che a = (p+q)/2 e b = (p- q)/2.
Siano dati due punti A1 e A2; costruire il punto A3 simmetrico di 0 rispetto al punto medio tra A1 e A2; costruire il punto A4 simmetrico di 0 rispetto al punto medio tra A2 e A3; .... Che successione di punti si ottiene? Per A2 = A3 = 1 la successione si chiama di Fibonacci.
Costruire solo con simmetrie i primi dieci elementi di una successione aritmetica: a+b, a+2b, a+3b, ....
Usando solo la macro X2 costruire i primi dieci elementi della successione a, a2, a3, a4, ... e i primi dieci elementi della successione a, a- 2, a- 3, a- 4, ...
Usando le macro-costruzioni disponibili per le operazioni, costruire i primi dieci elementi di una successione geometrica ab, ab2, ab3, ab4, ...
Costruire la media aritmetica semplice, la media geometrica, la media, armonica, la media quadratica tra due punti.
Dato un punto Y, costruire il punto Xg tale che Y sia la media geometrica tra 1 e Xg, costruire il punto Xa tale che Y sia la media armonica tra 1 e Xa.
Dati A e C costruire B in modo che C sia media geometrica di A e B; costruire B in modo che C sia media armonica di A e B.
Considerare la costruzione seguente:
A quale formula corrisponde il punto X ?
È possibile vedere la formula come media pesata di A e B ?
Comporre formule Si tratta di attività per imparare a leggere correttamente le formule, per "smontarle" e "rimontarle" anche in relazione a un preciso scopo, per disincentivare ricorrenti errori di calcolo.
Queste attività vanno affrontate facendo uso esclusivo delle macro-costruzioni fornite per le operazioni di base o delle macro-costruzioni la cui realizzazione è via via suggerita.
Costruire i punti a+b/c, (a+b)/c, (ac+b)/c.
Costruire sia il punto a/b +c/d sia il punto (a+c)/(b+d).
Costruire a+b2, (a+b)2 e a2+b2.
Costruire x3 facendo uso delle macro X2 e XY.
Costruire x5 facendo uso di entrambe le macro X2 e X3.
Costruire x6 facendo uso solo di entrambe le macro X2 e X3.
Costruire x16 facendo uso solo della macro X2, solo quattro volte.
Che formula si ottiene applicando la macro XY ai punti iniziali 0, u, a e b ?
Che formule si ottengono applicando la macro X+Y o la macro XY ai punti iniziali 0, 1, a e b cambiandone l’ordine ? E applicandole nell’ordine ai punti a, b, c e d ?
Costruire la funzione X ® AX+B e farne una macro.
Dati i punti a, x e b applicare a x la macro 1/X e poi al risultato ottenuto applicare la macro AX+B con A = a e B = b; scrivere la formula così ottenuta.
Dati i punti a, x e b costruire (a+bx)/x e confrontare con il punto precedente.
Dati i punti a, x e b applicare a x la macro AX+B con A=a e B=b e poi al risultato applicare la macro 1/X; confrontare con il punto precedentemente ottenuto.
Dati i punti a, b, c e x costruire ax²+bx+c usando solo la macro AX+B ( si applica la macro per ottenere ax+b e poi la si applica di nuovo ai punti iniziali ax+b, x e c ).
Dati i punti a, b, c , costruire il punto D/4 = (b/2)2 - ac e poi gli zeri del trinomio ax ²+bx+c applicando la nota formula algebrica ridotta ( si tratta di un lavoro che richiede particolare concentrazione e un uso opportuno di Edizione/Aspetto degli oggetti/Nascondi ).
Realizzare una macro per gli zeri del trinomio ax2+bx+c ( come sopra ).
Costruire i polinomi di III grado facendo uso unicamente della macro AX+B.
Costruire Ö (a2) e farne una macro |X|.
Costruire |- a|, |a+b| e |a|+|b|, |a- b| e |a|- |b|, |ab| e |a||b|, |a/b| con |a|/|b|.
Costruire max(x,y) = (|x- y|+x+y)/2; costruire analogamente min(x,y).
Costruire la funzione sign(x) = 1 sse x > 0, sign(x)= - 1 sse x < 0 ( basterà costruire x/|x| ).
Costruire la funzione f(x) = x- b se x < a , f(x) = x- b se x > a.
Osservare relazioni e raffigurarle dinamicamente Si tratta di attività per visualizzare l'azione di un operatore sull'ordine, per evitare regole sbagliate quanto naturali come quella della linearità, per visualizzare funzioni, per distinguere variabile indipendente da variabile dipendente, per distinguere il ruolo dei parametri da quello delle variabili, per risolvere equazioni e disequazioni, per esaminare condizioni e, addirittura, i connettivi per legarle.
Per affrontare le attività seguenti occorre costruire innanzitutto le formule in questione, trascinare poi lungo la retta reale il punto ( o i punti ) che rappresenta la variabile indipendente - cioè i punti base delle costruzioni - individuando dove cessano di esistere i valori dipendenti mediante quelle formule, osservando l’ordine nel quale i diversi punti si pongono sulla retta reale, considerando indizio di uguaglianza algebrica il fatto che due punti appaiono sovrapposti e sono valutati da Cabri con il messaggio Ambiguità.
Esaminare l’espressione (2a+a) /a al variare di a.
Osservare l'ordine tra a, 1/a, 1/a2 nei casi a < - 1, - 1£ a< 0, 0< a< 1, a ³ 1.
Verificare che, detta Ma la media armonica di due punti, Mg la media geometrica, M la media aritmetica e Mq la media quadratica, si ha:
Ma £ Mg £ M £ Mq.
Costruire la media pesata di a e b, pesando a con il valore k e b con il valore h; studiarla al variare dei pesi.
Costruire i punti Ö a2 e (Ö a)2 e confrontarli al variare di a.
Costruire i punti Ö (ab) e Ö a × Ö b e confrontarli al variare di a e b.
Confrontare Ö (a+b) e Ö a+Ö b al variare di a; quando coincidono i due punti ?
Confrontare |a+b| con |a| + |b| al variare di a; quando coincidono i due punti ? e quando |a+b| > |a| + |b| ?
Descrivere il campo di esistenza per la variabile x nella funzione Ö (x+a) e per i valori della funzione.
Risolvere le disequazioni : – x < 0, 1/x > 1, |x| > a.
Osservare che la funzione max(sign(x),sign(y)) vale 1 sse ( x> 0 Ú y> 0).
A che condizione corrisponde min(sign(x),sign(y)) = 1 ? e la condizione min(sign(x- a),sign(x- b)) = 1 ?
Posto che pÞ q equivale a Ø pÚ q, trovare una espressione algebrica equivalente a x2> 0 Þ x > 0 e verificare se è vera.
Variare x in modo che ax+b si annulli ; costruire - b/a verificando che coincide con tale valore di x.
Costruire ax+b e cx+d; trovare x in modo che ax+b = cx+d.
Per quali punti x si ha ax+b < 0 ?
Per quali punti x si ha che (x- x1)(x- x2) > 0 ?
Osservare che al variare uniformemente di t sulla retta il punto at+b si muove di moto uniforme.
Che tipo di moto segue il punto p = at²+bt+c al variare uniformemente di t sulla retta ?
Come si trasforma il segmento di estremi x e x+1 nella trasformazione AX+B al variare di x ? e nella trasformazione AX2+BX+C ?
Studiare ax²+bx+c > 0 ( I metodo: variare x fino a che ax²+bx+c non si sovrappone a 0, costruire il punti x1 e trascinarlo fino a sovrapporlo a x - marcando così una radice del trinomio - .... II metodo: servirsi della macrocostruzione per gli zeri del trinomio ).
Studiare una funzione discontinua come x ® x× sign(x+a) + b.
Realizzare il grafico di (ax+b)/(cx+d) nel piano cartesiano ( costruire l’asse y; ... costruire la bisettrice del primo quadrante; costruire il simmetrico di (ax+b)/(cx+d) rispetto alla bisettrice; .... ).
Riferimenti bibliografici
Gardner M., 1980, Il numero casuale W e il problema dell’arresto, in: R.Magari (a cura di), Numeri, caso e sequenze, Le Scienze Quaderni, n° 45, Milano 1988, pp.22-26.
Ricci R., 1994, Algebra con Cabri, CABRI-IRRSAE ER, Quaderno n° 5.