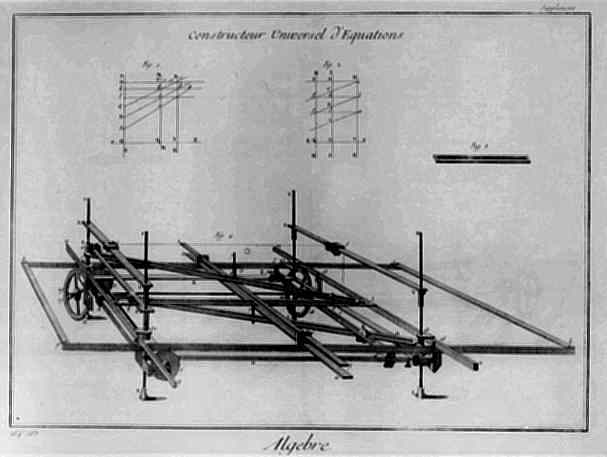
Risolutore universale di equazioni

Roberto Ricci

docente di Matematica e Fisica al Liceo Scientifico "A. Righi" di Bologna

La figura illustra l'apparecchio ideato nel 1751 e chiamato da Diderot nell'Encyclopedie: 'Constructeur universelle d'equations' che possiamo tradurre con 'Risolutore universale di equazioni'. Il meccanismo si compone di aste rigide che a un estremo possono scorrere lungo un'asse, quello delle ordinate, per rappresentare opportunamente i coefficienti dell'equazione e che, collegate a due altre aste rigide disposte perpendicolarmente, una fissa per l'unità e l'altra scorrevole in direzione delle ascisse, possono tracciare il grafico del polinomio in questione. Gli zeri si trovano come intersezioni con l'asse delle ascisse.

Con Cabri è semplice riprodurre il funzionamento della macchina, e così è possibile rendersi conto del funzionamento e riflettere per comprenderne le ragioni matematiche .

Supponiamo di voler risolvere l'equazione ax³+bx²+cx+d = 0. Tracciato un sistema di assi cartesiani ortogonali si fissa l'unità sull'asse x, quindi sull'asse y i punti d'=d, c'=d'+c, b'=c'+b, a'=b'+a. E così via nel caso di grado maggiore di 3.

Si traccia la retta passante per (0,b') e (1,a'). Ad essa appartiene il punto (x, ax+b'). Si traccia la retta per (0,c') e (1,ax+b'). Ad essa appartiene il punto (x,ax²+bx+c'). Si traccia la retta per (0,d') e (1,ax²+bx+c'). Ad essa appartiene il punto (x,ax³+bx²+cx+d).

E' interessante osservare anche, mediante qualche semplice calcolo, che le rette per b', d' e c' hanno pendenza rispettivamente a, ax+b, ax²+bx+c, che quindi P ha ordinata ax³+bx²+cx+d.

Orbene allo scorrere di x lungo l'asse delle ascisse, P traccia il luogo di punti y=ax³+bx²+cx+d e quindi coincide con x quando quest'ultimo è uno zero.

Possiamo dire che il dispositivo è un tracciatore di grafici di polinomi di grado n.

Tuttavia esiste un altro modo ancora più semplice, riproducibile con Cabri, per risolvere questo stesso problema, nell'ipotesi preliminare non restrittiva che a=1. Tale metodo risale a Bombelli.

Si crea innanzitutto una retta OA. Si costruisce per O la perpendicolare ad OA, e su questa si crea il punto B. Si costruisce poi per B la perpendicolare ad OB, e su questa si crea il punto C. Si costruisce inoltre per C la perpendicolare a BC, e su quest'ultima retta si crea il punto D. La costruzione prosegue analogamente per grado superiore a 3. Infine si crea un punto variabile x sulla retta OB, si crea il segmento di estremi in questo punto e in A, poi si costruisce da questo punto la retta perpendicolare al segmento. Costruito il punto in comune tra questa retta e BC, da questo si costruisce la perpendicolare alla stessa retta.

Quando l'intersezione tra quest'ultima retta e CD coincide con D, allora x è una radice dell'equazione di terzo grado x³+bx²+cx+d quando, nel riferimento cartesiano di centro O e assi BO e AO, si ha che A(0,-1), B(-b,0), C(-b,-c), D(-b+d,-c).

Nel caso di figura l'equazione ha tutte e tre le radici reali.

Si può spiegare il metodo con considerazioni ancora analitiche:
y = -x₀(x-x₀) e y=-c+(x+b-d)/x₀ sono le equazioni della prima e dell'ultima retta costruita.
Se queste due rette si intersecano in un punto di BC dovrà aversi -x₀(-b-x₀) =-c+(-b+b-d)/x₀, il che appunto x₀³+bx₀²+cx₀+d = 0