Moto dei pianeti intorno al Sole
Roberto Ricci
Liceo Scientifico "A.Righi"- Bologna
Premessa
È noto che Newton, nell'evoluzione del suo pensiero matematico, sviluppò una crescente repulsione nei confronti del metodo cartesiano, sempre più convinto che la fusione tra geometria e aritmetica avrebbe portato alla perdita della semplicità di cui consiste l'eleganza della geometria.
Nei suoi Principia, dove si propone in particolare di dimostrare le leggi del moto dei corpi celesti di Keplero collegandole ad attrazioni inversamente proporzionali ai quadrati delle distanze tra pianeti e sole, scrive:
... la descrizione delle linee rette e dei circoli su cui si fonda la Geometria, riguarda la Meccanica. La Geometria non insegna la descrizione di tali linee ma le postula. Richiede che, prima di pervenire ai suoi ammaestramenti, si sappiano già descrivere; dopo di che insegna come si risolvano dei problemi per mezzo di tali operazioni. Perciò, descrivere la retta ed il circolo non sono problemi geometrici. Postulata la loro soluzione come cosa pertinente alla Meccanica, la Geometria ne insegna l'uso. Ed è gloria della Geometria il rendere tanto fruttuosi così pochi principii. Dunque la Geometria, fondata sulla prassi meccanica, non è altro che quella parte della Meccanica Universale che tratta e dimostra l'arte della accurata misurazione. E poiché le arti manuali intendono principalmente a muovere i corpi, ciò ha fatto sì che il volgo riferisse alla Geometria la grandezza, ed alla Meccanica il moto. Onde la Meccanica Razionale sarebbe la scienza che tratta e dimostra accuratamente i movimenti che risultano da forze qualsiasi, e le forze che si richiedono per moti qualsiasi.
Gli Antichi - i quali consideravano la Gravità (che non è potenza manuale) solo come peso, per la forza che è necessaria a rimuoverlo - coltivarono questa parte della Meccanica nelle cinque potenze spettanti alle arti manuali. ... [Newton, 1687]
Tuttavia le dimostrazioni geometriche con le quali cerca di riabilitare o nobilitare i risultati ottenuti col metodo dell'analisi infinitesimale non erano di facile lettura; la loro lettura è ancora più disagevole oggi, quando la conoscenza sintetica di numerose proprietà delle coniche è stata via via sostituita da conoscenze essenziali da integrare con abilità di calcolo algebrico. Perfino un fisico del XX secolo del calibro di Richard Feynman ammette qualche difficoltà a seguire la strada proposta da Newton. Affascinato tuttavia dal metodo sintetico alternativo a quello oggi usuale basato sul calcolo differenziale, escogita un metodo elementare, già proposto anche da Maxwell [1877] che a sua volta cita Hamilton, per dimostrare che dall'ipotesi di attrazioni gravitazionali centrali e inversamente proporzionali ai quadrati delle distanze segue una traiettoria ellittica. Questo metodofu proposto in una famosa lezione a matricole del California Institute of Technology ed è il soggetto di un libro affascinante di Goodstein e Goodstein [1997], dove si legge ad esempio:
Sto per farvi vedere quella che chiamerò una dimostrazione elementare. Ma "elementare" non vuol dire facile da capire. "Elementare" vuol dire che è necessario saper ben poco in anticipo per poterla capire, ma ci vuole una quantità infinita d'intelligenza. …Naturalmente, una dimostrazione elementare di questo tipo potrebbe anche consistere nell'insegnarvi l'analisi matematica e poi fare la dimostrazione. Questa sarebbe però una dimostrazione più lunga di quella che voglio presentarvi. …ma per vostro diletto e profitto voglio farvi fare un giro in un fuoristrada di grande eleganza… Così descriveremo questo fatto con ragionamenti essenzialmente geometrici, perché io non ho idea, non ho precisamente un'idea, di cosa voglia dire "con ragionamenti puramente geometrici"; ma lo faremo con ragionamenti essenzialmente geometrici, e vedrete come ce la caveremo bene. [Goodstein e Goodstein, 1997, pp. 141-142]
In questo scritto seguiremo in parte questo metodo elementare utilizzando come strumenti riga e compasso, ma implementati in ambiente informatico:
… descrivere la retta ed il circolo non sono problemi geometrici. Postulata la loro soluzione come cosa pertinente a Cabri Geometry II, la Geometria ne insegna l'uso. Ed è gloria della Geometria il rendere tanto fruttuosi così pochi principii. …
In particolare risulterà utile, insieme alla dinamicità delle figure digitalizzate sullo schermo del computer, la possibilità di realizzare movimenti con il comando Animazione dell'ambiente Cabri.
Un tale argomento può essere considerato uno degli migliori esempi di interdisciplinarietà tra matematica e fisica da proporre alla fine di un terzo anno di liceo scientifico.
Analisi intuitiva di un moto
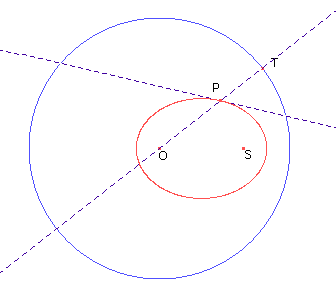
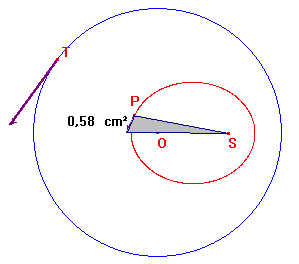
Consideriamo inizialmente il moto circolare uniforme di un punto T intorno a un punto O. Fissato un punto qualsiasi S e costruito il punto P intersezione tra la retta OT e l'asse di ST, proponiamoci di studiare il moto di P.

Dopo aver selezionato dal menu l'opzione Animazione, e indicato poi il punto T vincolato alla circonferenza, Cabri anima il disegno: T si muoverà a velocità uniforme mentre P sembra muoversi proprio come un pianeta in orbita ellittica intorno al Sole S, con velocità al perielio maggiore di quella all'afelio.
La sua traiettoria, luogo dei punti equidistanti da S e dalla circonferenza, è un'ellisse o un'iperbole a seconda che S sia interno o esterno al cerchio. Infatti nel primo caso OP+PS = OP+PT = OT è costante mentre nel secondo caso OP- PS = OP- PT = OT è costante. Inoltre l'asse di ST è tangente alla traiettoria. Infatti, preso a riferimento il caso in cui S è un punto interno al cerchio, tra i punti di questa retta, P è l'unico per cui OP+PS=OT è minima dal momento che T, simmetrico di S rispetto alla retta in questione, è allineato con O e P.
La velocità di P, che dev'essere un vettore tangente alla traiettoria di P, avrà quindi direzione dell'asse di ST e dipenderà dalla velocità di modulo costante con cui si muove T. Possiamo costruire il vettore velocità di P proiettando sulla tangente alla sua traiettoria quel vettore che ne rappresenterebbe la velocità nel caso in cui P seguisse il moto circolare uniforme del segmento OT.
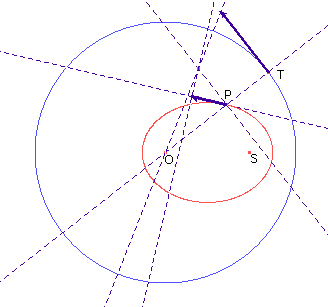
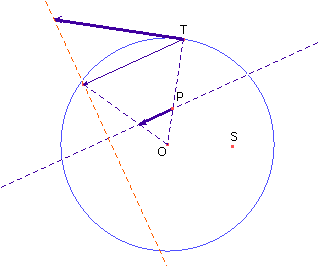
Tra parentesi, notiamo che il moto con cui P si avvicina a O è uguale a quello con cui si allontana da S dal momento che OP+PS deve restare costante; in particolare la velocità con cui P si avvicina a O è uguale a quella con cui si allontana da S.
A questo punto, per giungere allo studio dell'accelerazione, costruiamo la traiettoria descritta dal vettore che rappresenta la velocità di P, posto ad esempio con l'origine in S. La velocità con cui si muove questo vettore, la cui traiettoria sarà chiamata anche diagramma delle velocità di P, è evidentemente l'accelerazione di P.
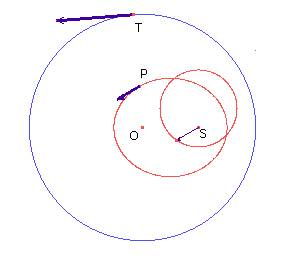
Con una certa evidenza il diagramma sembra essere una circonferenza.
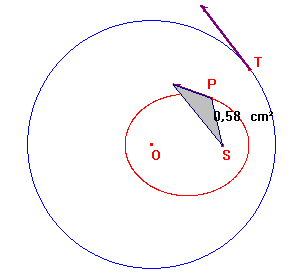
Per costruire infine la direzione dell'accelerazione del moto di P, cioè della velocità con cui varia la velocità di P, tangente al diagramma delle velocità, occorre conoscere il centro di tale presunta circonferenza. Costruendo le velocità all'afelio A e al perielio B, che hanno stessa direzione ma versi opposti, possiamo ottenere un suo diametro di lunghezza, come è facile verificare, uguale al modulo della velocità di T.
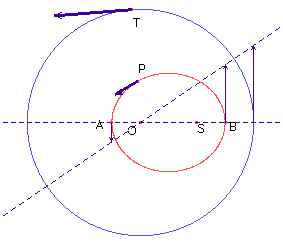 Riportati nel diagramma i due particolari vettori velocità all'afelio e al perielio, possiamo dunque costruire la circonferenza con quel diametro e convincerci ulteriormente attraverso la visualizzazione che essa coincide con il diagramma delle velocità.
Riportati nel diagramma i due particolari vettori velocità all'afelio e al perielio, possiamo dunque costruire la circonferenza con quel diametro e convincerci ulteriormente attraverso la visualizzazione che essa coincide con il diagramma delle velocità.
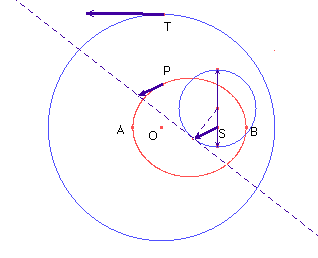
 Dopo aver costruito la tangente al diagramma velocità nel punto che rappresenta la velocità di P, cioè la direzione dell'accelerazione con cui si muove P, osserviamo che passa per la punta del vettore velocità di P; quindi la parallela a questa retta mandata da P passa per S, ovvero l'accelerazione di P è centripeta verso S.
Dopo aver costruito la tangente al diagramma velocità nel punto che rappresenta la velocità di P, cioè la direzione dell'accelerazione con cui si muove P, osserviamo che passa per la punta del vettore velocità di P; quindi la parallela a questa retta mandata da P passa per S, ovvero l'accelerazione di P è centripeta verso S.
Dimostrazioni geometriche
A questo punto, per confermare i risultati ottenuti finora attraverso un'intuizione potenziata da Cabri, è più che mai necessario produrre dimostrazioni geometriche, anche per poter verificare che l'accelerazione del moto segue una legge di inversa proporzionalità nei confronti del quadrato della distanza da S.
Iniziamo constatando, sulla base delle costruzioni precedenti, che c'è proporzionalità tra le velocità di P all'afelio e al perielio e le rispettive distanze da O; questo suggerisce una similitudine tra la figura formata dalla traiettoria di T e dal punto S e quella formata dal diagramma delle velocità di P e ancora del punto S.
Per facilitare le dimostrazioni modifichiamo allora l'unità per le velocità in modo che il vettore velocità di T abbia modulo pari al diametro della traiettoria di T. Ora il diagramma delle velocità, ruotato di un angolo retto, sembra coincidere con la circonferenza traiettoria di T.
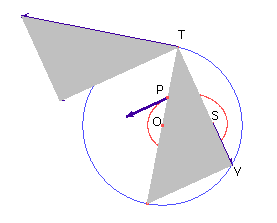
Sempre sulla base della figura, per similitudini tra triangoli, possiamo constatare inoltre che, detto vP il modulo della velocità di P,
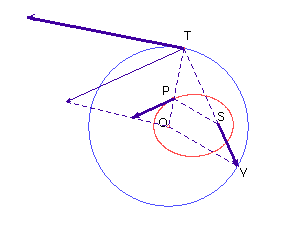
Rimane infine da provare che l'accelerazione di P, che ha per direzione quella della tangente al diagramma velocità in V ruotato di un angolo retto, cioè la direzione di OV, che è la stessa di PS, è inversamente proporzionale al quadrato della distanza di P da S. Affronteremo dunque lo studio del moto di V quando T si muove uniformemente, in particolare della sua velocità, che conduce all'accelerazione di P.
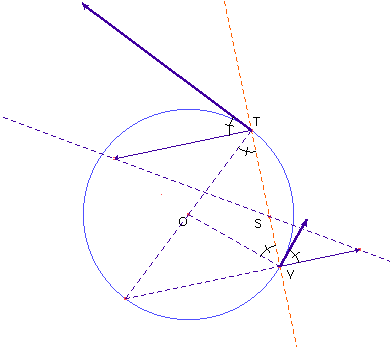
Tale velocità, di modulo aP, si può costruire a partire dal moto di rotazione della retta TV intorno a S. La velocità con cui T ruota intorno a S è la componente della sua velocità circolare in direzione normale alla retta TV; come già detto, il suo modulo è esattamente la lunghezza del segmento TV. La velocità con cui V ruota intorno a S si ottiene a sua volta per proporzionalità: è perpendicolare alla retta TV ed ha modulo pari a TV× SV / TS; la componente di questo vettore tangenziale alla circonferenza traiettoria di T è la velocità di V e quindi ha modulo aP.
Detto vT il modulo della velocità di T, per similitudine tra i triangoli delle velocità in T e in V si ha aP : (TV× SV/TS) = TV : vT ovvero aP = TV2× SV / (TS× vT).
Considerata la proporzione TV : TS = OT : PS e ricordato che il prodotto TS× SV è costante, la potenza di S rispetto alla circonferenza, si ottiene infine la relazione di proporzionalità inversa tra aP e il quadrato di PS.
Riferimenti bibliografici
Newton I., 1687, Principii di Filosofia Naturale: Teoria della Gravitazione, a cura di F.Enriques e U.Forti, Casa Editrice Alberto Stock, Roma 1925, pp. 22-23.
Maxwell J.C., 1877, Materia e moto, Università degli studi di Pavia, 1993, pp.75-80.
Goodstein D.L., Goodstein J.R., Il moto dei pianeti intorno al sole, Zanichelli, Bologna 1997
Indicazioni per le figure
Tutte le figure sono realizzate con Cabri-Géomètre II, vers. 1.0. Nel seguito è indicato, nell'ordine delle figure nel testo, l'elenco delle istruzioni per ciascuna costruzione.
Fig.1.
Creare circonferenza di centro O;
creare punto S;
creare punto T sulla circonferenza;
costruire asse di ST;
creare retta OT;
creare punto P intersezione tra OT e asse di ST;
costruire luogo di P al variare di T.
Fig.2.
Sulla base della costruzione descritta per Fig.1:
costruire retta perpendicolare da T a OT;
creare vettore di origine T e estremo T1 sulla retta appena costruita (velocità di T);
creare retta OT1;
costruire retta perpendicolare da P a OT;
creare punto P1 intersezione tra OT1 e la retta perpendicolare da P a OT;
costruire retta perpendicolare da P1 all'asse di ST;
creare il punto P2 intersezione tra la retta appena costruita e l'asse di ST;
creare vettore di origine P e estremo P2 (velocità di P).
Fig.3.
Sulla base della costruzione descritta in Fig.1 (costruzione alternativa alla precedente):
costruire retta perpendicolare da T a OT;
creare vettore di origine T e estremo T1 sulla retta appena costruita (velocità di T);
costruire retta parallela da T all'asse di ST;
costruire retta perpendicolare da T1 all'asse di ST;
creare punto T2 intersezione tra le due rette appena costruite;
creare retta OT2;
creare punto P1 intersezione tra OT2 e l'asse di ST;
creare vettore di origine P e estremo P1 (velocità di P).
Fig.4.
Sulla base della costruzione descritta in Fig.3:
creare retta OS;
creare punto A1 e punto B1 intersezione tra OS e la circonferenza;
costruire punto medio A di A1S e punto medio B di B1S;
creare segmento OT1;
costruire con compasso la circonferenza di centro B1 e raggio OT1;
costruire retta perpendicolare da B1 a OS;
creare punto B2 intersezione tra circonferenza e retta appena costruite;
creare vettore B1B2 (velocità del moto circolare in B1);
creare retta OB2;
costruire retta perpendicolare da A a OS;
creare punto A2 intersezione tra OB2 e la retta appena costruita;
creare vettore di origine A e estremo A2 (velocità del moto di P all'afelio);
costruire retta perpendicolare da B a OS;
creare punto B3 intersezione tra OB2 e la retta appena costruita;
creare vettore di origine B e estremo B3 (velocità del moto di P al perielio).
Fig.5.
Sulla base della costruzione descritta in Fig.4:
costruire punto SA traslazione di S associata al vettore velocità del moto di P all'afelio;
costruire punto SB traslazione di S associata al vettore velocità del moto di P al perielio;
costruire punto SP traslazione di S associata al vettore velocità del moto di P;
creare vettore SSA, vettore SSB e vettore SSP;
costruire punto medio tra SA e SB;
creare circonferenza di centro in questo punto e passante per SA;
costruire luogo di SP al variare di T (diagramma delle velocità di P).
Fig.6.
Sulla base della costruzione descritta in Fig.5:
creare segmento di estremo SP raggio della circonferenza diagramma delle velocità;
costruire retta perpendicolare da SP al raggio.
Fig.7.
È la Fig.5 con alcuni elementi nascosti.
Figg. 8 e 9.
Sulla base della costruzione descritta in Fig.3:
creare triangolo di lato coincidente col vettore velocità di P e vertice in S;
effettuare riempimento del triangolo con colore opportuno;
misurare area del triangolo.
Fig.10.
Sulla base della costruzione descritta in Fig.1:
costruire retta perpendicolare da T a OT;
costruire punto TO corrispondente di T nella simmetria centrale di centro O;
creare circonferenza di centro T e passante per TO;
creare punto T1 intersezione tra la circonferenza appena creata e la perpendicolare da T a OT;
creare vettore di origine T e estremo T1 (vettore velocità di T nell'unità opportuna);
costruire retta parallela da T all'asse di ST;
costruire retta perpendicolare da T1 all'asse di ST;
creare punto T2 intersezione tra le due rette appena costruite;
creare retta OT2;
creare punto P1 = OT2 Ç asse di ST;
creare vettore di origine P e estremo P1 (vettore velocità di P nell'unità opportuna);
creare retta ST;
creare punto V intersezione tra la retta TS e la circonferenza data di centro O;
creare triangolo TT1T2 e triangolo TTOV;
effettuare riempimento dei triangoli appena costruiti con opportuni colori.
Fig. 11.
Sulla base della costruzione descritta per Fig.10:
creare segmento OT2, segmento OT, segmento OV e segmento PS;
Fig. 12.
Sulla base della costruzione descritta per Fig.10:
creare retta T2S;
creare retta TOV;
creare punto V1 intersezione tra le rette appena costruite
creare vettore di origine V e estremoV1;
costruire retta perpendicolare da V ad OV;
costruire retta perpendicolare da V1 alla retta appena costruita;
creare punto V2 intersezione tra le rette appena costruite;
creare vettore di origine V e estremo V2 (vettore velocità di V, accelerazione di P ruotata di un angolo retto).