Solidi di volume massimo

  
 

 
Il fusto di un albero ha la forma di un tronco di cono. Determinare le dimensioni del prisma a base quadrata di volume massimo che si può ricavare dal tronco dato.
 
 
Chiamati con l il lato della base e h l'altezza del prisma poniamo

Dalla similitudine dei triangoli rettangoli di figura si ha

Da cui segue l'espressione del volume da rendere massimo

Si tratta di una funzione di terzo grado che tende a più infinito per x tendente a meno infinito e tendente a meno infinito per x tendente a più infinito. La cubica è tangente nell'origine all'asse delle ascisse e taglia lo stesso asse in x = R, poiché nell'intervallo compreso tra x = 0 e  x = R  la funzione è positiva nello stesso intervallo ammette massimo. Dalla derivata di questa funzione

si ha il massimo per

quindi le misure del prisma di volume massimo

Tutto questo nell'ipotesi che sia

Se

allora il lato l è quello del quadrato inscritto nella base minore del tronco di cono, di raggio r, mentre l'altezza h del prisma coincide con l'altezza H del tronco stesso.
Determinare le misure del cono di volume massimo che può essere inscritto in un segmento di paraboloide di data altezza. Il vertice del cono è nel centro della base del segmento di paraboloide.
 
 
Consideriamo il paraboloide ottenuto dalla rotazione intorno all'asse delle ascisse della parabola di equazione

Per ottenere il segmento dato mandiamo un piano ortogonale all'asse delle ascisse passante per il punto (B, 0) che è anche il vertice del cono inscritto. Posto OA = x e  OB = H , mandato il piano passante per (A, 0) che tagliando il paraboloide definisce la base del cono si ha che il volume del cono di cui si chiede di massimizzare il volume è dato da

La curva da studiare è una parabola con la concavità rivolta verso il basso che ha un massimo nel vertice cioè in

Dunque il cono di volume massimo ha il raggio di base, l'altezza e il volume che valgono rispettivamente

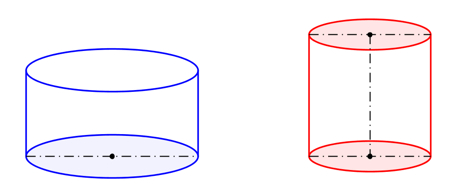
Determinare le dimensioni di un bicchiere cilindrico a base circolare, aperto verso l'alto, di data superficie totale S e di volume massimo. Confrontare le misure di questo recipiente con quelle di un barattolo cilindrico, munito di coperchio, avente la medesima superficie totale e anch'esso di volume massimo.
 
Se S è la superficie totale di entrambi i solidi detto r il raggio della base e h l'altezza del cilindro per includere entrambi i casi in una'unica trattazione scriviamo

dove per n = 1 si ha il bicchiere e per n = 2 il barattolo. Il volume da rendere massimo è dato da

dove le limitazioni vengono dal fatto che sia il raggio che il volume debbono essere entrambi positivi o al più nulli.
Si tratta di studiare un arco di una cubica che si annulla agli estremi dell'intervallo considerato e che è positiva in quell'intervallo quindi ammette massimo. Dalla derivata prima di questa funzione

si ha il massimo in

In altri termini a parità di superficie totale il bicchiere ha volume massimo quando la sua altezza è pari al raggio della base mentre il barattolo ha volume massimo quando l'altezza è pari al diametro della base.