Triangoli simili
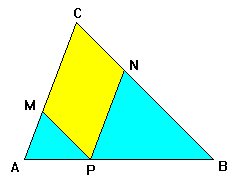
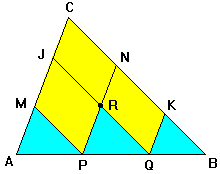
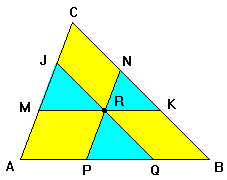
Dalla rivista belga "Correspondance mathématique et physique" del 1838 diretta A. Quetelet (1796-1874) prendiamo un problema geometrico. Lo stesso problema fu ripreso e ampliato nel 1859 nei "Nouvelles annales de Mathématiques" dei francesi Olry Terquem (1782-1862) e Camille Gerono (1799-1891) . Rifaremo l'intero percorso in tre tappe dimostrando un teorema su una figura semplice per applicarlo poi a figure più complesse.
   
Dato il triangolo ABC e preso il punto P sul lato AB mandiamo da P le parallele ai lati che intersecano CA in M e BC in N. Dette: S l'area del triangolo ABC, S1 e S2 le aree dei triangoli APM e PBN, e T  l'area del parallelogrammo PNCM. Dalla similitudine dei triangoli ABC, APM e PBN si ha che
se allora
da cui
quindi
Sul lato AB del triangolo ABC prendiamo ora due punti P e Q e mandiamo le parallele ai lati. Si formano in questo caso tre triangoli APM, PQR e QBK  simili al triangolo dato e tre parallelogrammi: MPRJ, RQKN e JRNC. Dette S1, S2 e S3 le aree dei tre triangoli e T1, T2 e T3 le aree dei tre parallelogrammi, applicando il teorema precedente ai triangoli AQJ, PBN ed andando per differenza con l'area del triangolo S si ricava che
da cui
Prendiamo ora un punto R interno al triangolo ABC e mandiamo le parallele ai lati, si ottengono angora tre triangoli simili a quello dato e tre parallelogrammi. Dette S1, S2 e S3 le aree dei triangoli PQR, RKN e MRJ, T1, T2 e T3 le aree dei parallelogrammi QBKR, RNCJ e APRM; applicando ai triangoli AQJ, PBN e MKC il primo teorema si ottiene ancora
Lo stesso problema è risolto in modo leggermente diverso da Alexander Bogomolny sul suo sito web - Cut The Knot - nella pagina dal titolo "A Multiplicative Identity of Areas in a Triangle" . La soluzione è corredata da delle applet Java interessanti.