In questa pagina sono raccolte le soluzioni degli "IntelliGiochi".
I lupi mannari morti ritrovati sono esattamente tre. Per arrivare a questa conclusione bisogna però seguire un ragionamento logico che è abbastanza semplice da capire, ma piuttosto difficile da impostare senza avere nessun ulteriore aiuto. Cominciamo col supporre che ci sia un solo lupo mannaro in città, quest'ultimo, durante la prima notte non vede in giro nessun altro lupo, in quanto appunto egli è l'unico. Dunque, dato che è a conoscenza della presenza di almeno un lupo, capisce che l'unico lupo è egli stesso, e quindi si ucciderebbe la prima notte. Questo però non succede, quindi dobbiamo scartare l'ipotesi che ci sia un solo lupo. Supponiamo allora che i lupi siano due. La prima notte, ognuno di essi vede esattamente un lupo mannaro (l'altro) pensando che ce ne sia uno soltanto, e quindi, per il ragionamento fatto in precedenza, pensa che questo si ucciderà nel corso della prima notte, ma ciò ovviamente non avviene. Pertanto la notte successiva (la seconda) i due lupi si incontrano di nuovo ed entrambi capiscono quindi che ci deve essere un secondo lupo ma dato che ne vedono solo uno, capiscono di essere anch'essi dei lupi, e si ucciderebbero nella seconda notte. Dato che la seconda notte nessuno si è ucciso, dobbiamo supporre che i lupi siano tre. Allora ognuno di questi tre, sulla base di quanto detto fin qui, penserà che gli altri due si uccideranno la seconda notte, ma la terza notte li rivede ancora e quindi capisce che ce ne deve essere un terzo, e che quel terzo deve essere lui, e quindi si uccide. Il ragionamento può essere generalizzato e possiamo quindi dire che se ci fossero n lupi, questi si ucciderebbero dopo n notti.
2. La scacchiera mutilata
(tratto da "Enigmi e giochi matematici" di Martin Gardner)
È impossibile ricoprire la scacchiera ridotta (dopo l'eliminazione delle due caselle d'angolo opposte) con 31 pezzi di domino e lo si dimostra facilmente. I due angoli diagonalmente opposti sono dello stesso colore. Perciò togliendoli si ottiene una scacchiera con due caselle di un colore in più rispetto all'altro colore Ogni pezzo di domino ricopre due caselle di colori differenti, in quanto solo caselle di colori sono fra loro adiacenti. Dopo aver ricoperto 60 caselle con 30 pezzi di domino, rimarrebbero due caselle dello stesso colore che non possono essere contigue e perciò venir coperte con l'ultimo, unico pezzo.
La risposta è: un gatto. Questa risposta è sorprendente, in quanto si è indotti a pensare che allungando una circonferenza così lunga di una percentuale tanto insignificante, provochi un aumento del raggio altrettanto insignificante. Invece questo non è vero, poichè l'incremento subito dal raggio dipende solo dalla lunghezza del pezzo di corda aggiunto e non dal raggio della circonferenza iniziale. Detto questo, il calcolo è veramente immediato. Infatti, indicando con R il raggio terrestre, con PI la costante pi greco e con C=2*PI*R la circonferenza, si ha che la distanza tra la corda e la superficie terrestre vale: d = (C+1)/(2*PI) - R = 1/(2*PI) che vale circa 16 centimetri, e quindi ci può passare sotto un gatto.
Le 1000 lire non sono finite da nessuna parte. Infatti il gioco è intenzionalmente posto con lo scopo di ingannare colui che deve risolverlo. La spiegazione è molto semplice: si può facilmente osservare che le 27000 complessivamente sborsate dai tre amici, sono state così suddivise: 25000 lire al direttore del ristorante e le restanti 2000 sono la mancia data al cameriere.
La risposta corretta è: 99 giorni. La soluzione di questo gioco è veramente molto semplice, infatti, se al centesimo giorni la ninfea ha ricoperto tutto il lago, il giorno precedente ne copriva evidentemente la metà, dato che ogni giorno la superficie della foglia raddoppia.
Per ottenere il risultato voluto, bisogna innanzitutto riempire la tanica da 5 e quindi trasferirne 3 litri nell'altra. In questo modo saranno rimasti 2 litri in quella da 5. Successivamente si svuota quella da 3 e si trasferiscono i 2 litri precedenti dalla tanica da 5 a quella da 3. A questo punto riempiamo di nuovo quella da 5 e trasferiamo 1 litro in quella da 3 in modo da riempire quest'ultima. Il risultato ottenuto sarà quello di avere 4 litri di acqua nella tanica più grande.
Per la risoluzione generale di problemi come questo risulta utile rappresentare ogni configurazione del contenuto delle due taniche con una coppia di numeri (n1,n2) che rappresentano i litri d'acqua contenuti rispettivamente nei due recipienti. A questo punto bisogna costruire un grafo, i cui nodi sono appunto costituiti dalle coppie descritte in precedenza. A partire da ogni nodo bisogna poi costruire i nuovi nodi che si possono ottenere applicando una delle regole seguenti:
7. Acqua e vino
(tratto da "Enigmi e giochi matematici" di Martin Gardner)
La risposta è che c'è tanto vino nell'acqua quanta acqua nel vino. Il fatto divertente in questo problema è la straordinaria quantità di informazioni irrilevanti fornite. Non è necessario conoscere quanto liquido vi sia in ogni caraffa, quanto ne sia trasferito da una all'altra o quanti trasferimenti vengono fatti. Non ha importanza se le miscele sono ben mescolate o meno. Non è nemmeno essenziale che i due recipienti contengano la stessa quantità di liquido all'inizio! La sola condizione importante è che alla fine ogni caraffa deve contenere esattamente la stessa quantità di liquido dell'inizio. Ottenuto ciò è ovvio che se manca una quantità x di vino dalla caraffa del vino, lo spazio prima occupato da tale quantità deve ora essere occupato da una quantità x di acqua.
Per quanto riguarda il secondo problema invece, prescindendo dalla quantità di vino in una caraffa e di acqua nell'altra e da quanto liquido viene trasferito avanti e indietro ad ogni stadio (purchè il liquido non vada tutto in una sola delle caraffe), è impossibile raggiungere un punto in cui la percentuale di vino della miscela sia eguale in entrambe. Questo lo si può dimostrare con un semplice ragionamento induttivo. Se la caraffa A contiene una concentrazione più alta di vino che B, un trasferimento da A a B lascerà A con la concentrazione maggiore. Similmente un trasferimento da B a A (da una miscela inferiore ad una più forte) lascerò certamente B più debole. Dato che per ogni trasferimento si verifica uno di questi due casi, ne segue che la caraffa A deve sempre contenere una miscela a percentuale più alta di vino che B. Il solo modo di rendere uguali le concentrazioni è di versare tutto il contenuto di una caraffa nell'altra. In questa soluzione vi è però un'idea errata. Essa ammette che i liquidi siano infinitamente divisibili, mentre sono composti di molecole discrete.
La mosca ha percorso esattamente 120 km. La risoluzione è molto semplice e praticamente non richiede nessun calcolo. Se si osserva che i due treni viaggiano alla velocità relativa di 200 km/h, si conclude che lo scontro avviene esattamante un'ora dopo la partenza. La mosca ha quindi viaggiato a velocità costante per un'ora, percorrendo 120 km.
Ecco la soluzione di questo semplice gioco. Ovviamente esistono anche altre soluzioni simmetriche a questa. La difficoltà sostanziale che molti incontrano nell'affrontare questo problema è dovuta al fatto che essi pensano di dover risolvere il problema di coprire i punti di questo quadrato senza uscirne.
10. Il ciclista
(tratto da "Matematica dell'incertezza" di Giuliano Spirito)
La risposta corretta è: 30 km/h. La risposta più frequente che viene data a questo problema è è invece 40 km/h, basata sul fatto che che il ciclista ha percorso esattamente metà del cammino alla velocità (media) di 20 km/h e esattamente l'altra metà alla velocità (media) di 60 km/h; ma ciò nondimeno, la risposta è errata, giacché procedendo in discesa ad una velocità tripla rispetto a quella tenuta in salita il nostro atleta ha pedalato per un tempo triplo alla velocità di 20 km/h rispetto al tempo in cui è andato a 60 km/h. La risposta corretta è dunque data (3 x 20 + 60) / 4 = 30 km/h. Bisogna cioè tenere conto del peso relativo di ciascuna delle medie.
La soluzione si ottiene disponendo i sei fiammiferi in modo da costruire un tetraedro regolare, cioè una piramide a base triangolare, dunque una figura tridimensionale. La maggior parte dei soggetti non riesce a risolvere questo problema perchè pensa che i fiammiferi vadano disposti su un piano.
12. La diagonale del rettangolo
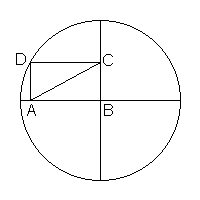È immediato notare che la lunghezza di AC vale 1. Infatti la linea AC è una diagonale del rettangolo e l'altra diagonale BD è evidentemente il raggio del cerchio che vale 1. Dato che le due diagonali sono uguali, anche AC è lunga 1.
Il problema può essere risolto rompendo un solo anello e precisamente il terzo. In questo modo si ha disposizione un anello singolo (appunto il terzo), una catena con due anelli (il primo e il secondo) ed una con quattro anelli (dal quarto al settimo). Con questi tre pezzi è possibile formare ogni combinazione numerica da uno a sette. La chiave del problema sta nel fatto che il conoscente riceva un anello il primo giorno e nei successivi abbia un anello in più ogni giorno e non che riceva un nuovo anello ogni giorno. In pratica si procede nel seguente modo: il primo giorno viene dato il primo anello, il secondo giorno vengono dati gli anelli 1-2 e viene restituito il 3, il terzo giorno viene di nuovo aggiunto l'anello 3, il quarto giorno vengono dati gli anelli 4-5-6-7 e restituiti gli anelli 1-2 e 3; e così via. La difficoltà che in genere viene incontrata nella risoluzione di questo problema è dovuta all'errata interpretazione dell'espressione "un anello al giorno", che viene capita nel senso letterale e che quindi non tiene conto delle possibili restituzioni.
Nel caso dei 30 anelli in 30 giorni, la soluzione si ottiene spezzando gli anelli 3, 9 e 21. Così facendo infatti si ottengono delle catene di lunghezza: 1, 1, 1, 2, 5, 9, 11. Combinando opportunamente i precedenti si possono ottenere tutti i numeri da 1 a 30.
Per risolvere il problema sono sufficienti due pesate. Denominiamo le palline con A, B, C e D. Per individuare quella diversa si può procedere nel seguente modo: nella prima pesata si mettono a confronto A e B, e si annota se si è avuto equilibrio oppure no; nella seconda pesata invece si toglie una pallina (ad esempio B) e la si sostituisce con un'altra, cioè si confronta A con C, ed anche in questo caso si controlla se c'è o meno equilibrio. A questo punto, a seconda degli esiti delle due pesate si possono avere quattro diversi casi, in ognuno dei quali è possibile individuare la pallina di peso diverso. La soluzione è riportata nella tabella che segue.
| Pesata 1 | Pesata 2 | Pallina diversa |
|---|---|---|
| Equilibrio | Equilibrio | |
| Equilibrio | Squilibrio | |
| Squilibrio | Equilibrio | |
| Squilibrio | Squilibrio |
| Terna | Somma |
|---|---|
| 36-1-1 | 38 |
| 18-2-1 | 21 |
| 12-3-1 | 16 |
| 9-4-1 | 14 |
| 9-2-2 | 13 |
| 6-6-1 | 13 |
| 6-3-2 | 11 |
| 4-3-3 | 10 |
Il mucchio di monete false può essere identificato con una sola pesata. Prendete una moneta dal primo mucchio; due dal secondo, tre dal terzo e così via sino a tutte e dieci le monete dell'ultimo mucchio. Pesate ora l'intera collezione di campioni sulla bilancia. Il peso in più del dovuto in grammi, corrisponde al numero spettante al mucchio di monete false. Per esempio, se il gruppo di monete pesa in totale sette grammi in più del dovuto, il mucchio falso deve essere il settimo, dal quale sono state prese sette monete (ognuna pesante un grammo in più della moneta vera). Anche se vi fosse un undicesimo mucchio di dieci monete, il procedimento descritto sarebbe ancora valido, in quanto un eccesso di peso nullo indicherebbe che il mucchio falso è l'ultimo rimasto.
Secondo problema: bastano due pesate. Siano le monete ABCDEFGHI. Si mettano ABC su un piatto e DEF sull'altro. Si danno tre casi, in ognuno dei quali abbiamo tre sottocasi. La soluzione completa è riportata in tabella.
| Pesata 1 | Pesata 2 | Moneta falsa |
|---|---|---|
| ABC = DEF | G = H | I |
| G < H | H | |
| G > H | G | |
| ABC < DEF | D = E | F |
| D < E | E | |
| D > E | D | |
| ABC > DEF | A = B | C |
| A < B | B | |
| A > B | A |
Terzo problema: bastano tre pesate. Supponiamo che le monete siano ABCDEFGHIJKL. Come primo tentativo, si confrontino ABCD e EFGH. Anche in questo caso in base al risultato della prima pesata, si effettuano quelle successive. La soluzione completa è in tabella:
| Pesata 1 | Pesata 2 | Pesata 3 | Moneta falsa |
|---|---|---|---|
| ABCD = EFGH | AI = JK | L < A | L (+ leggera) |
| L > A | L (+pesante) | ||
| L = A | Impossibile | ||
| AI < JK | J = K | I (+ leggera) | |
| J < K | K (+ pesante) | ||
| J > K | J (+ pesante) | ||
| AI > JK | J = K | I (+ pesante) | |
| J < K | J (+ leggera) | ||
| J > K | K (+leggera) | ||
| ABCD > EFGH | AEI = BCH | F = G | D (+ pesante) |
| F < G | F (+ leggera) | ||
| F > G | G (+ leggera) | ||
| AEI < BCH | A = I | H (+ leggera) | |
| A < I | Impossibile | ||
| A > I | A (+ pesante) | ||
| AEI > BCH | B = C | E (+ leggera) | |
| B < C | C (+ pesante) | ||
| B > C | B (+ pesante) | ||
| ABCD < EFGH | AEI = BCH | F = G | D (+ leggera) |
| F < G | G (+ pesante) | ||
| F > G | F (+ pesante) | ||
| AEI < BCH | A = I | H (+ pesante) | |
| A < I | A (+ leggera) | ||
| A > I | Impossibile | ||
| AEI > BCH | B = C | E (+ pesante) | |
| B < C | B (+ leggera) | ||
| B > C | C (+ leggera) |
Il trucco qui è il fatto che il presentatore non apre una porta a caso, ma ne sceglie una con una capra. Supponiamo di avere scelto la prima porta: in questo momento abbiamo probabilità 1/3 che l'auto sia dietro una qualunque porta. Nei due casi in cui l'auto sia nella porta 2 o 3, il presentatore apre rispettivamente la porta 3 o 2, e se noi cambiamo scelta vinciamo (probabilità 2/3); se avevao scelto la porta giusta, lui ne apre a caso una delle altre (probabilità 1/6 per ciascuna) e se noi cambiamo perdiamo (probabilita` 1/3). Quindi ci conviene cambiare porta.
La risposta tipica è "sette", perchè la parola "quattro" ha sette lettere. Infatti in tutti i casi la controparola era il numero di lettere che componevano la parola d'ordine. Come già scritto, le risposte possibili sono infinite...
A e B attraversano il ponte e B torna indietro (4 min).
C e D attraversano il ponte e A torna indietro (15 min).
A e B attraversano il ponte e sono tutti in salvo (17 min).
Il barbone aveva raccolto 22 mozziconi con i quali ha confezionato 5 sigarette con l'avanzo di due mozziconi. Coi 7 mozziconi rimasti dopo aver fumato le prime 5, ha fabbricato un'altra sigaretta con l'avanzo di 3 mozziconi. Dopo averla fumata rimane con 4 mozziconi coi quali costruisce la settima sigaretta. Alla fine quindi gli rimane 1 mozzicone.
La risposta è che potete arrivare fino alla Luna, e a dire la verità anche un po' oltre. Infatti ad ogni piegamento, lo spessore raddoppia, perciò dopo 42 piegamenti, lo spessore totale sarà 242 volte lo spessore iniziale, che equivale a circa 440000 km che è, come vedete, maggiore della distanza terra-luna che è approssimativamente 385000 km. A questo punto verrebbe da chiedersi perchè si spendono tanti soldi per le missioni spaziali, quando basterebbe andare alla cartoleria all'angolo, comprare un foglio di carta, piegarlo 42 volte e poi salirci sopra!
La risposta è che passano 200 camion ogni ora. L'automobilista viaggia ad una velocità relativa rispetto ai camion di 40 km/h. Perciò in mezz'ora, percorre 20 km, sempre rispetto ai camion. Questo significa che in un tratto di strada lungo 20 km, ci sono 50 camion, e cioè che ogni camion dista dal successiva 400 m (=20km/50). Dunque tra il passaggio di un camion e l'altro, passano 18 secondi (=0,400/80=0,005 ore) pertanto in un'ora ne passano 200 (=3600/18).
|
Ultimo aggiornamento: