MIKY & GENNY
CONICHE ---> INDICE
Ellisse,
iperbole e parabola sono state definite come luogo dei punti per i
quali è costante il rapporto, eccentricità, delle
distanze da un punto, fuoco, e da una retta, direttrice.
A seconda che l'eccentricità sia minore, maggiore o uguale all'unità, si ha rispettivamente l'ellisse, l'iperbole e la parabola.
Ellisse, iperbole e parabola vengono dette anche sezioni coniche, o semplicemente coniche, in quanto esse si possono ottenere come sezioni del cono circolare retto a doppia falda con un piano scelto opportunamente, non passante per il suo vertice, perchè in tal caso la conica sarebbe degenere, cioè costituita da due rette.
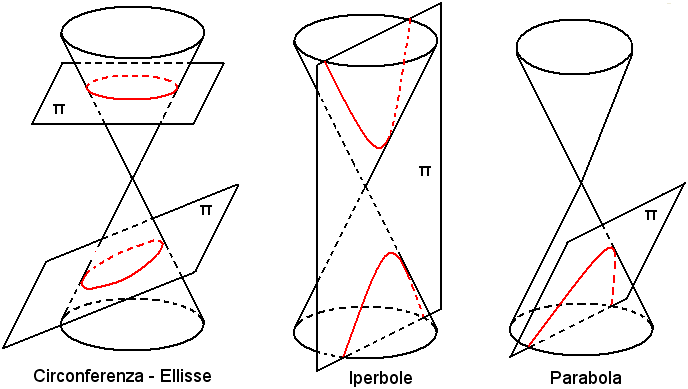
L'iperbole si ottiene come intersezione della superficie conica con un piano secante π che incontra su entrambe le falde della superficie tutte le generatrici tranne due, al cui piano secante è parallelo. L'angolo degli asintoti risulta uguale a quello delle due generatrici parallele al piano π ed è, in particolare, doppio dell'angolo di apertura del cono, quando il piano π è parallelo all'asse del cono stesso. Segue che l'iperbole è equilatera, solo quando l'angolo di apertura del cono è di 45° gradi ed il piano secante è parallelo all'asse del cono.
La parabola si ottiene tagliando la superficie conica con un piano π che taglia tutte le generatrici di una falda, tranne una, al quale il piano è parallelo.
Si ricorda che in precedenza si sono ottenute le equazioni canoniche delle coniche, cioè si sono considerate le coniche in posizioni particolari, e precisamente l'iperbole, la parabola e l'ellisse aventi per centro l'origine degli assi, ad eccezione della parabola conica non a centro, e gli assi, asse per la parabola, coincidenti o paralleli agli assi di riferimento.
Se si considera la conica in una posizione qualsiasi, rispetto agli assi di riferimento, la sua equazione è:
(1) ax2 + bxy + cy2 + mx + ny + p = 0.
Tale equazione rappresenta una conica degenere, cioè costituita da una coppia di rette o da una retta doppia, se il polinomio del primo membro è il prodotto di due polinomi di primo grado, ossia l'equazione (1) è del tipo:
(ax + by + c)(a'x + b'y + c') = 0.
L'equazione completa di secondo grado rappresenta:
-un'ellisse, se b2 - 4ac < 0,
-una parabola, se b2 - 4ac = 0,
-un'iperbole, se b2 - 4ac > 0.
Se nella (1) m = n = 0, cioè mancano i termini di primo grado, la conica ha per centro l'origine delle coordinate; se nella (1) b = 0, cioè manca il termine rettangolare, gli assi della conica sono paralleli agli assi di riferimento; infine, se nella (1) mancano i termini lineari ed il termine rettangolare, si ha l'equazione canonica delle coniche già studiate.
Determinazione degli asintoti di una curva
La relazione b2 - 4ac rappresenta il discriminante di un'equazione del tipo
(2) ax2 + bxy + cy2 = 0,
ottenuta dalla (1) uguagliando a zero il complesso dei termini di secondo grado.
Essa fornisce le direzioni asintotiche della conica. Una conica, dunque, si chiama iperbole, parabola o ellisse, a seconda che ammetta due, una o nessuna direzione asintotica. Le rette, per il centro della conica, aventi come coefficienti angolari i valori determinati dalla (2), sono gli asintoti della conica.
In generale:
-le direzioni asintotiche, o punti all'infinito, di una curva si ottengono uguagliando a zero il complesso dei termini di grado più elevato che appaiono nell'equazione della curva.
Esempi
1)-Determinare gli asintoti della cubica x3 + y3 - 3xy = 0, folium di Cartesio.
I punti all'infinito della cubica sono dati dall'equazione x3 + y3 = 0, ottenuta uguagliando a zero il complesso dei termini di grado più elevato, cioè quelli di terzo grado.
Risolvendo x3 + y3 = 0 rispetto a y/x, si ha:
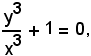
ossia
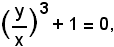
equazione reciproca di prima classe e grado dispari; essa ammette l'unica radice reale y/x = -1. La curva passa per il punto all'infinito della retta x + y = 0, bisettrice del II e IV quadrante. Per determinare l'asintoto, cioè la retta parallela alla x + y = 0 e tangente alla cubica, si considera una retta generica parallela alla bisettrice x + y = 0, la cui equazione è del tipo x + y + h = 0. S'interseca la curva con tale retta:
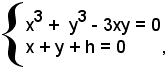
cioè
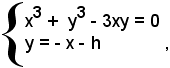
sostituendo nella prima equazione del sistema al posto di y il valore dato dalla seconda, si ha:
x3 + (-x - h)3 - 3x(- x - h) = 0,
sviluppando
x3 - x3 - 3hx2 - 3h2x - h3 + 3x2 + 3hx = 0,
riducendo e ordinando
3(1 - h)x2 + 3h(1 - h)x - h3 = 0.
Si rilevi come l'equazione risolutiva del sistema si è abbassata di grado, il sistema è di terzo grado, e ciò significa che una soluzione va all'infinito, cioè la retta x + y + h = 0 ha con la cubica due intersezioni proprie ed una, all'infinito, impropria.
Quindi la curva passa per il punto all'infinito della retta x + y + h = 0.
Per determinare l'asintoto, tangente alla cubica nel punto all'infinito, s'impone che l'equazione risolutiva si abbassi ulteriormente di grado; ciò si verifica se è nullo il primo coefficiente dell'equazione stessa, cioè se 1 - h = 0, da cui h = 1; sostituendo tale valore di h nell'equazione x + y + h = 0 si ottiene l'equazione dell'asintoto x + y + 1 = 0.
2)-Determinare gli asintoti reali della cubica x(x2 + y2) - y2 = 0, cissoide di Diocle.
I punti all'infinito di tale cubica si ottengono uguagliando a zero il complesso dei termini di grado più elevato che appaiono nell'equazione, cioè quelli di terzo grado; essi sono, dunque, dati da:
x(x2 + y2) = 0,
da cui
x = 0 e (x2 + y2) = 0,
quest'ultimi immaginari.
La cubica passa per il punto all'infinito dell'asse y.
Una retta generica passante per il punto all'infinito dell'asse y, cioè parallela all'asse y, ha equazione: x = h. S'interseca ora la curva con tale retta, si ha:
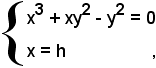
da cui
A seconda che l'eccentricità sia minore, maggiore o uguale all'unità, si ha rispettivamente l'ellisse, l'iperbole e la parabola.
Ellisse, iperbole e parabola vengono dette anche sezioni coniche, o semplicemente coniche, in quanto esse si possono ottenere come sezioni del cono circolare retto a doppia falda con un piano scelto opportunamente, non passante per il suo vertice, perchè in tal caso la conica sarebbe degenere, cioè costituita da due rette.

L'iperbole si ottiene come intersezione della superficie conica con un piano secante π che incontra su entrambe le falde della superficie tutte le generatrici tranne due, al cui piano secante è parallelo. L'angolo degli asintoti risulta uguale a quello delle due generatrici parallele al piano π ed è, in particolare, doppio dell'angolo di apertura del cono, quando il piano π è parallelo all'asse del cono stesso. Segue che l'iperbole è equilatera, solo quando l'angolo di apertura del cono è di 45° gradi ed il piano secante è parallelo all'asse del cono.
La parabola si ottiene tagliando la superficie conica con un piano π che taglia tutte le generatrici di una falda, tranne una, al quale il piano è parallelo.
Si ricorda che in precedenza si sono ottenute le equazioni canoniche delle coniche, cioè si sono considerate le coniche in posizioni particolari, e precisamente l'iperbole, la parabola e l'ellisse aventi per centro l'origine degli assi, ad eccezione della parabola conica non a centro, e gli assi, asse per la parabola, coincidenti o paralleli agli assi di riferimento.
Se si considera la conica in una posizione qualsiasi, rispetto agli assi di riferimento, la sua equazione è:
(1) ax2 + bxy + cy2 + mx + ny + p = 0.
Tale equazione rappresenta una conica degenere, cioè costituita da una coppia di rette o da una retta doppia, se il polinomio del primo membro è il prodotto di due polinomi di primo grado, ossia l'equazione (1) è del tipo:
(ax + by + c)(a'x + b'y + c') = 0.
L'equazione completa di secondo grado rappresenta:
-un'ellisse, se b2 - 4ac < 0,
-una parabola, se b2 - 4ac = 0,
-un'iperbole, se b2 - 4ac > 0.
Se nella (1) m = n = 0, cioè mancano i termini di primo grado, la conica ha per centro l'origine delle coordinate; se nella (1) b = 0, cioè manca il termine rettangolare, gli assi della conica sono paralleli agli assi di riferimento; infine, se nella (1) mancano i termini lineari ed il termine rettangolare, si ha l'equazione canonica delle coniche già studiate.
Determinazione degli asintoti di una curva
La relazione b2 - 4ac rappresenta il discriminante di un'equazione del tipo
(2) ax2 + bxy + cy2 = 0,
ottenuta dalla (1) uguagliando a zero il complesso dei termini di secondo grado.
Essa fornisce le direzioni asintotiche della conica. Una conica, dunque, si chiama iperbole, parabola o ellisse, a seconda che ammetta due, una o nessuna direzione asintotica. Le rette, per il centro della conica, aventi come coefficienti angolari i valori determinati dalla (2), sono gli asintoti della conica.
In generale:
-le direzioni asintotiche, o punti all'infinito, di una curva si ottengono uguagliando a zero il complesso dei termini di grado più elevato che appaiono nell'equazione della curva.
Esempi
1)-Determinare gli asintoti della cubica x3 + y3 - 3xy = 0, folium di Cartesio.
I punti all'infinito della cubica sono dati dall'equazione x3 + y3 = 0, ottenuta uguagliando a zero il complesso dei termini di grado più elevato, cioè quelli di terzo grado.
Risolvendo x3 + y3 = 0 rispetto a y/x, si ha:
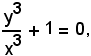
ossia
equazione reciproca di prima classe e grado dispari; essa ammette l'unica radice reale y/x = -1. La curva passa per il punto all'infinito della retta x + y = 0, bisettrice del II e IV quadrante. Per determinare l'asintoto, cioè la retta parallela alla x + y = 0 e tangente alla cubica, si considera una retta generica parallela alla bisettrice x + y = 0, la cui equazione è del tipo x + y + h = 0. S'interseca la curva con tale retta:
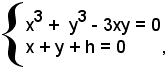
cioè
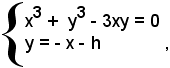
sostituendo nella prima equazione del sistema al posto di y il valore dato dalla seconda, si ha:
x3 + (-x - h)3 - 3x(- x - h) = 0,
sviluppando
x3 - x3 - 3hx2 - 3h2x - h3 + 3x2 + 3hx = 0,
riducendo e ordinando
3(1 - h)x2 + 3h(1 - h)x - h3 = 0.
Si rilevi come l'equazione risolutiva del sistema si è abbassata di grado, il sistema è di terzo grado, e ciò significa che una soluzione va all'infinito, cioè la retta x + y + h = 0 ha con la cubica due intersezioni proprie ed una, all'infinito, impropria.
Quindi la curva passa per il punto all'infinito della retta x + y + h = 0.
Per determinare l'asintoto, tangente alla cubica nel punto all'infinito, s'impone che l'equazione risolutiva si abbassi ulteriormente di grado; ciò si verifica se è nullo il primo coefficiente dell'equazione stessa, cioè se 1 - h = 0, da cui h = 1; sostituendo tale valore di h nell'equazione x + y + h = 0 si ottiene l'equazione dell'asintoto x + y + 1 = 0.
2)-Determinare gli asintoti reali della cubica x(x2 + y2) - y2 = 0, cissoide di Diocle.
I punti all'infinito di tale cubica si ottengono uguagliando a zero il complesso dei termini di grado più elevato che appaiono nell'equazione, cioè quelli di terzo grado; essi sono, dunque, dati da:
x(x2 + y2) = 0,
da cui
x = 0 e (x2 + y2) = 0,
quest'ultimi immaginari.
La cubica passa per il punto all'infinito dell'asse y.
Una retta generica passante per il punto all'infinito dell'asse y, cioè parallela all'asse y, ha equazione: x = h. S'interseca ora la curva con tale retta, si ha:
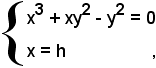
da cui
h2 + hy2 - y2 = 0;
ordinando, si ha
(h - 1)y2 + h3 = 0.
Per determinare l'asintoto, s'impone che l'equazione si abbassi di grado, ciò si verifica se è nullo il primo coefficiente dell'equazione stessa, cioè se:
h - 1 = 0,
da cui
h = 1.
L'equazione dell'asintoto è dunque x = 1.
In generale:
-una curva passa per il punto all'infinito dell'asse x o y, e quindi avrà asintoti paralleli all'asse x o y, se nell'equazione la variabile x o y, si presenta di grado inferiore rispetto al grado dell'equazione.
Le equazioni degli asintoti paralleli all'asse x o y, si ottengono direttamente uguagliando a zero il coefficiente della x o y, di grado più elevato esistente nell'equazione. Ovviamente il coefficiente è un polinomio in y o x.
Nell'esempio (2), ordinando l'equazione della cubica x3 + xy2 - y2 = 0, si rileva che la variabile y si presenta di grado inferiore, secondo, rispetto al grado dell'equazione, terzo. La curva passa quindi per il punto all'infinito dell'asse y e quindi ha un asintoto parallelo all'asse y.
La sua equazione si ottiene uguagliando a zero il coefficiente della y di grado più elevato esistente nell'equazione. Ordinando l'equazione rispetto a tale variabile, si ottiene:
(x - 1)y2 + x3 = 0;
quindi
x - 1 = 0
è l'equazione dell'asintoto.
3)-Quando si è trattata l'iperbole, essa si è considerata con gli asintoti paralleli agli assi, la cui equazione è del tipo:
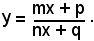
Tale equazione si può scrivere:
Poichè, sia la variabile x, sia la variabile y si presentano di grado inferiore, primo, rispetto al grado dell'equazione, secondo, l'iperbole ha quindi gli asintoti paralleli agli assi di riferimento.
Ordinando l'equazione rispetto alla variabile x, si ha:
(ny - m)x + qy - p = 0;
uguagliando a zero il coefficiente della x, cioè ny - m = 0, si ha l'equazione dell'asintoto orizzontale; ordinando l'equazione rispetto alla variabile y, si ha:
(nx + q)y - mx - p = 0;
uguagliando a zero il coefficiente della y, cioè nx + q = 0, si ha l'equazione dell'asintoto verticale.
ordinando, si ha
(h - 1)y2 + h3 = 0.
Per determinare l'asintoto, s'impone che l'equazione si abbassi di grado, ciò si verifica se è nullo il primo coefficiente dell'equazione stessa, cioè se:
h - 1 = 0,
da cui
h = 1.
L'equazione dell'asintoto è dunque x = 1.
In generale:
-una curva passa per il punto all'infinito dell'asse x o y, e quindi avrà asintoti paralleli all'asse x o y, se nell'equazione la variabile x o y, si presenta di grado inferiore rispetto al grado dell'equazione.
Le equazioni degli asintoti paralleli all'asse x o y, si ottengono direttamente uguagliando a zero il coefficiente della x o y, di grado più elevato esistente nell'equazione. Ovviamente il coefficiente è un polinomio in y o x.
Nell'esempio (2), ordinando l'equazione della cubica x3 + xy2 - y2 = 0, si rileva che la variabile y si presenta di grado inferiore, secondo, rispetto al grado dell'equazione, terzo. La curva passa quindi per il punto all'infinito dell'asse y e quindi ha un asintoto parallelo all'asse y.
La sua equazione si ottiene uguagliando a zero il coefficiente della y di grado più elevato esistente nell'equazione. Ordinando l'equazione rispetto a tale variabile, si ottiene:
(x - 1)y2 + x3 = 0;
quindi
x - 1 = 0
è l'equazione dell'asintoto.
3)-Quando si è trattata l'iperbole, essa si è considerata con gli asintoti paralleli agli assi, la cui equazione è del tipo:
Tale equazione si può scrivere:
nxy - mx + qy - p = 0.
Poichè, sia la variabile x, sia la variabile y si presentano di grado inferiore, primo, rispetto al grado dell'equazione, secondo, l'iperbole ha quindi gli asintoti paralleli agli assi di riferimento.
Ordinando l'equazione rispetto alla variabile x, si ha:
(ny - m)x + qy - p = 0;
uguagliando a zero il coefficiente della x, cioè ny - m = 0, si ha l'equazione dell'asintoto orizzontale; ordinando l'equazione rispetto alla variabile y, si ha:
(nx + q)y - mx - p = 0;
uguagliando a zero il coefficiente della y, cioè nx + q = 0, si ha l'equazione dell'asintoto verticale.