MIKY & GENNY
DISCUSSIONE DEI PROBLEMI DI SECONDO GRADO NEL PIANO CARTESIANO ---> INDICE
1)-Risolvere il sistema:
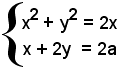
e discutere la realtà e il segno delle radici al variare di a, che si suppone negativo.
Casi particolari
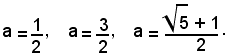
La prima equazione del sistema rappresenta una circonferenza di centro C(1, 0), raggio 1 e tangente all'asse x nell'origine O.
Poichè la circonferenza è tutta contenuta nel semipiano x > 0, le ascisse delle eventuali soluzioni sono tutte positive.
La seconda equazione del sistema rappresenta una retta r, la cui intercetta sull'asse x è un segmento 2a doppio dell'intercetta sull'asse y.
Al variare di a, si ha un fascio di rette parallele, fascio improprio.
Essendo per ipotesi a > 0, si considerano solo le rette del fascio le cui intercette con l'asse y, q = 2a, siano positive.
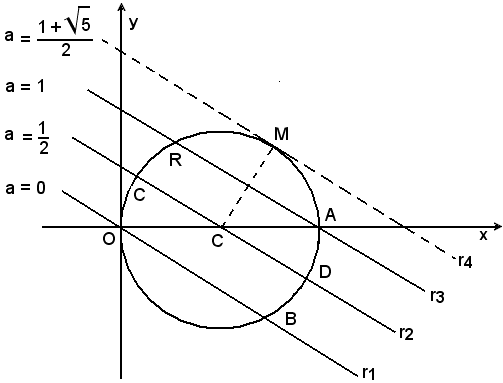
Si indicano con r1, r2, r3, rispettivamente, le rette del fascio passanti per i punti O(0, 0), C(1, 0), A(2, 0); queste hanno, rispettivamente, equazioni:
r1) x + 2y = 0 (a = 0),
r2) x + 2y = 1 (a = 1/2),
r3) x + 2y = 2 (a = 1).
La retta x + 2y = 2a è tangente alla circonferenza quando la sua distanza dal centro C(1, 0) è uguale al raggio r = 1, ossia:
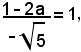
da cui
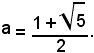
L'equazione della retta r4 è:
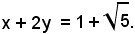
Quindi, per r variabile nella striscia limitata da r1 e r2, ossia per 0 < a < 1/2, delle due intersezioni della retta con la circonferenza, una appartiene al primo quadrante e l'altra al secondo; il sistema ammette, allora, due soluzioni e delle y una è positiva e l'altra negativa.
Per r variabile tra r2 e r3, ossia per 1/2 < a < 1, si hanno soluzioni come nel caso precedente.
Per r variabile tra r3 e r4, ossia per
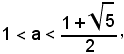
le due intersezioni retta-circonferenza appartengono al primo quadrante; le y ad esse relative sono positive.
Per
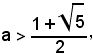
non si hanno intersezioni reali ed il sistema non ha soluzioni reali.

2)-Risolvere il sistema:
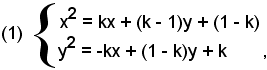
tenendo presente che qualunque sia il valore di k, ammette la soluzione x = 1, y = 0. Determinare poi per quale valore del parametro i valori x, y delle soluzioni risultano reali e concordi, oppure reali e discordi.
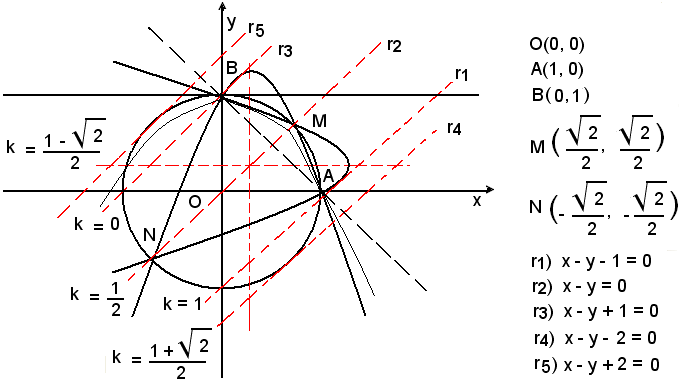
Nel caso particolare di k = 1/2, interpretando x ed y come coordinate cartesiane di un punto del piano, si traccino i grafici di ciascuna delle due equazioni del sistema.
Il sistema dato si può scrivere:
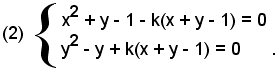
La prima equazione del sistema rappresenta un fascio di parabole individuato dalle due coniche fondamentali x2 + y - 1 = 0, parabola, e dalla retta x + y - 1 = 0.
La seconda equazione del sistema rappresenta un fascio di parabole individuato dalle due coniche fondamentali y2 - y =, parabola degenere costituita dalle due rette y = 0, asse x, e dalla y =1 e dalla retta x + y - 1 = 0.
I due fasci hanno in comune i due punti base A(1, 0) e B(0, 1).
Il sistema (1) è equivalente al sistema:
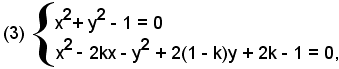
ottenuto sommando e sottraendo le equazioni del sistema (1).
Il sistema (3), risolvendo la seconda equazione di secondo grado rispetto alla variabile x, si può scrivere:
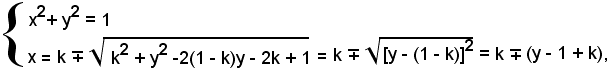
da cui si ricava
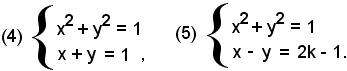
Il sistema (4) ha le soluzioni A(1, 0) e B(0, 1) già rilevate.
La discussione, dunque, del sistema (1) si riduce a quella del sistema (5).
La prima equazione del sistema (5) rappresenta la circonferenza avente il centro nell'origine O(0, 0) e raggio 1; la seconda equazione rappresenta un fascio improprio di rette parallele alla bisettrice del primo e terzo quadrante.
Le equazioni delle tangenti r4 e r5 sono, dunque, rispettivamente;
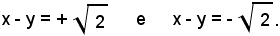
Il sistema (5) ammette soluzioni solo se la retta r) x - y = 2k - 1 incontra la circonferenza.
Quindi, per r variabile nella striscia limitata r5 e r3, ossia per
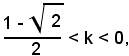
le due intersezioni retta-cerchio appartengono al secondo quadrante, quindi x ed y sono reali e discordi.
Per r variabile tra r3 e r2, ossia per
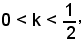
le due intersezioni retta-cerchio appartengono una al primo al quadrante e l'altra al terzo, quindi x ed y sono reali e concordi.
Per r variabile tra r2 e r1, ossia per
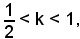
le intersezioni sono una al primo quadrante e l'altra al terzo, cioè come per
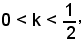
x ed y reali e concordi.
Per r variabile tra r1 e r4, ossia per
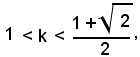
le due intersezioni retta-cerchio appartengono al quarto quadrante, quindi x rd y sono reali e discordi.
In conclusione, x ed y sono:
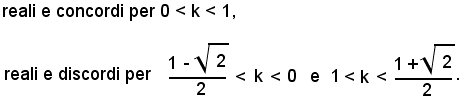
Nel caso in cui
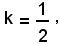
si hanno le due parabole di equazioni:
y = -2x2 + x + 1,
x = -2y2 + y + 1;
le loro intersezioni sono date dai punti:
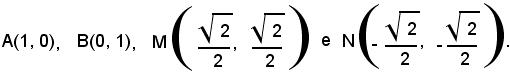
Si tralascia la considerazione dei seguenti casi particolari riportati in figura:
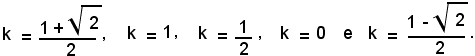
3)-Siano date le due curve di equazione:
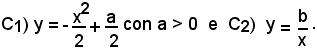
Si determini la relazione che deve sussistere fra a e b affinchè le curve s'incontrino nel punto P1 del primo quadrante, avente per ascissa 2. Indicate con P2 e P3 le ulteriori intersezioni delle due curve e condotte per esse le tangenti alla C2, si denotino con T2 e T3 i punti di tali tangenti che hanno ordinate nulle e si calcolino le ascisse. Si determini infine a, in modo che la distanza fra T2 e T3 sia 4k(a - 2), essendo k un numero positivo dato.
Se si ritiene opportuno, si può calcolare l'area della regione comune alla striscia determinata dalle parallele condotte all'asse x e alla curva C.
La curva C1 rappresenta una parabola avente per asse l'asse y, il vertice V(0, a/2) e interseca l'asse x nei punti
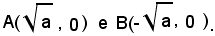
La curva C2 rappresenta un'iperbole equilatera avente per asintoti gli assi cartesiani e disposta nel primo e terzo quadrante, b > 0.
Affinchè le curve s'incontrino nel punto P1, di ascissa 2 del primo quadrante, occorre che sia b > 0.
Le coordinate dei punti d'intersezione delle due curve sono date dalle soluzioni del sistema formato dalle equazioni di C1 e C2:
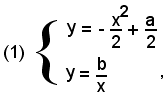
da cui si ricava, sostituendo il valore della y della prima equazione del sistema nella seconda,
(2) x3 - ax + 2b = 0.
Tale equazione ammette la radice x = 2, se:
4 - a + b = 0,
cioè
b = a - 4.
Affinchè P1 appartenga al primo quadrante, occorre, dunque, che:
b = a - 4 > 0,
cioè
a > 4.
Dopo aver osservato che dell'equazione (2) si conosce la radice x = 2 e la relazione tra a e b, ossia b = a - 4; applicando la regola di Ruffini all'equazione x3 - ax + 2a - 8 = 0, si ricava x3 - ax + 2a - 8 = (x - 2)(x2 + 2x + 4 - a), ossia:
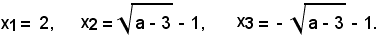
Sostituendo tali valori nella prima equazione del sistema (1), y = (a - 4)x, si hanno i valori delle ordinate. Si hanno quindi le coordinate degli altri due punti P2 e P3, d'intersezione delle curve C1 e C2:

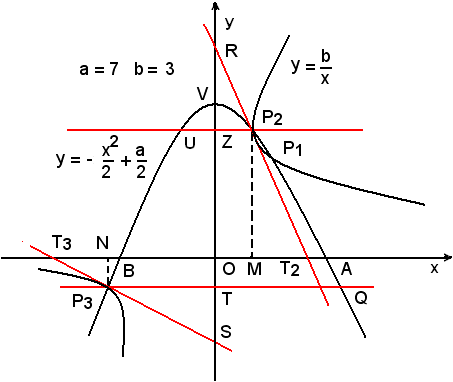
Le ascisse dei punti T2 e T3, intersezioni dell'asse x delle tangenti all'iperbole nei punti, rispettivamente, P2 e P3, si ricavano considerando che P2 e P3, punti di contatto delle tangenti, sono punti medi, rispettivamente, dei segmenti T2R e T3S e quindi anche le loro proiezioni suill'asse x, come anche sull'asse y, M e N sono punti medi dei segmenti OT2 e OT3. Si ha quindi:
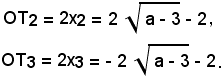
La distanza:
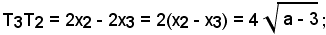
essa dev'essere
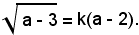
Elevando al quadrato, riducendo ed ordinando, si ottiene:
(3) k2a2 - (1 + 4k2)a + 4k2 + 3 = 0.
I valori di a soddisfacenti il nostro problema sono dati dalle soluzioni del sistema:
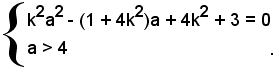
Tale sistema ammette l'unica soluzione a2 per
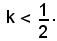
L'area della regione comune alla striscia determinata dalle rette y = y2 e y = y3 e dalla parabola, si ottiene come differenza dei segmenti parabolici P3VQ e UVP2, il cui valore è dato da:
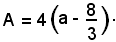
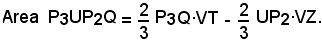
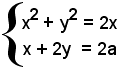
e discutere la realtà e il segno delle radici al variare di a, che si suppone negativo.
Casi particolari
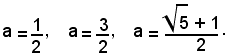
La prima equazione del sistema rappresenta una circonferenza di centro C(1, 0), raggio 1 e tangente all'asse x nell'origine O.
Poichè la circonferenza è tutta contenuta nel semipiano x > 0, le ascisse delle eventuali soluzioni sono tutte positive.
La seconda equazione del sistema rappresenta una retta r, la cui intercetta sull'asse x è un segmento 2a doppio dell'intercetta sull'asse y.
Al variare di a, si ha un fascio di rette parallele, fascio improprio.
Essendo per ipotesi a > 0, si considerano solo le rette del fascio le cui intercette con l'asse y, q = 2a, siano positive.

Si indicano con r1, r2, r3, rispettivamente, le rette del fascio passanti per i punti O(0, 0), C(1, 0), A(2, 0); queste hanno, rispettivamente, equazioni:
r1) x + 2y = 0 (a = 0),
r2) x + 2y = 1 (a = 1/2),
r3) x + 2y = 2 (a = 1).
La retta x + 2y = 2a è tangente alla circonferenza quando la sua distanza dal centro C(1, 0) è uguale al raggio r = 1, ossia:
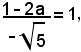
da cui
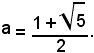
L'equazione della retta r4 è:
Quindi, per r variabile nella striscia limitata da r1 e r2, ossia per 0 < a < 1/2, delle due intersezioni della retta con la circonferenza, una appartiene al primo quadrante e l'altra al secondo; il sistema ammette, allora, due soluzioni e delle y una è positiva e l'altra negativa.
Per r variabile tra r2 e r3, ossia per 1/2 < a < 1, si hanno soluzioni come nel caso precedente.
Per r variabile tra r3 e r4, ossia per
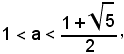
le due intersezioni retta-circonferenza appartengono al primo quadrante; le y ad esse relative sono positive.
Per
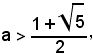
non si hanno intersezioni reali ed il sistema non ha soluzioni reali.

2)-Risolvere il sistema:
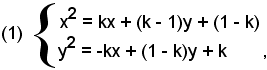
tenendo presente che qualunque sia il valore di k, ammette la soluzione x = 1, y = 0. Determinare poi per quale valore del parametro i valori x, y delle soluzioni risultano reali e concordi, oppure reali e discordi.

Nel caso particolare di k = 1/2, interpretando x ed y come coordinate cartesiane di un punto del piano, si traccino i grafici di ciascuna delle due equazioni del sistema.
Il sistema dato si può scrivere:
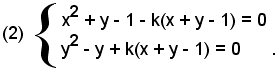
La prima equazione del sistema rappresenta un fascio di parabole individuato dalle due coniche fondamentali x2 + y - 1 = 0, parabola, e dalla retta x + y - 1 = 0.
La seconda equazione del sistema rappresenta un fascio di parabole individuato dalle due coniche fondamentali y2 - y =, parabola degenere costituita dalle due rette y = 0, asse x, e dalla y =1 e dalla retta x + y - 1 = 0.
I due fasci hanno in comune i due punti base A(1, 0) e B(0, 1).
Il sistema (1) è equivalente al sistema:
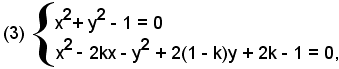
ottenuto sommando e sottraendo le equazioni del sistema (1).
Il sistema (3), risolvendo la seconda equazione di secondo grado rispetto alla variabile x, si può scrivere:
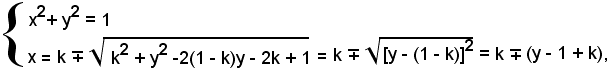
da cui si ricava
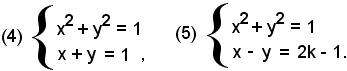
Il sistema (4) ha le soluzioni A(1, 0) e B(0, 1) già rilevate.
La discussione, dunque, del sistema (1) si riduce a quella del sistema (5).
La prima equazione del sistema (5) rappresenta la circonferenza avente il centro nell'origine O(0, 0) e raggio 1; la seconda equazione rappresenta un fascio improprio di rette parallele alla bisettrice del primo e terzo quadrante.
Si indicano con r1, r2, r3, rispettivamente, le rette del fascio passanti per i punti A(0, 1), O(0, 0), B(0, 1); queste hanno, rispettivamente, equazioni:
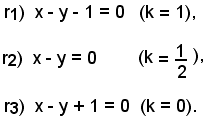
La retta x - y + 1 = 2k - 1 è tangente alla circonferenza quando la sua distanza dal centro O(0, 0) è uguale al raggio r = 1, ossia:

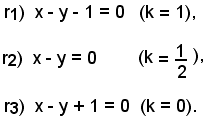
La retta x - y + 1 = 2k - 1 è tangente alla circonferenza quando la sua distanza dal centro O(0, 0) è uguale al raggio r = 1, ossia:

Le equazioni delle tangenti r4 e r5 sono, dunque, rispettivamente;
Il sistema (5) ammette soluzioni solo se la retta r) x - y = 2k - 1 incontra la circonferenza.
Quindi, per r variabile nella striscia limitata r5 e r3, ossia per
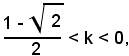
le due intersezioni retta-cerchio appartengono al secondo quadrante, quindi x ed y sono reali e discordi.
Per r variabile tra r3 e r2, ossia per
le due intersezioni retta-cerchio appartengono una al primo al quadrante e l'altra al terzo, quindi x ed y sono reali e concordi.
Per r variabile tra r2 e r1, ossia per
le intersezioni sono una al primo quadrante e l'altra al terzo, cioè come per
x ed y reali e concordi.
Per r variabile tra r1 e r4, ossia per
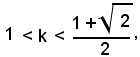
le due intersezioni retta-cerchio appartengono al quarto quadrante, quindi x rd y sono reali e discordi.
In conclusione, x ed y sono:
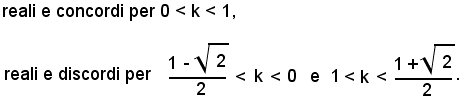
Nel caso in cui
si hanno le due parabole di equazioni:
x = -2y2 + y + 1;
le loro intersezioni sono date dai punti:
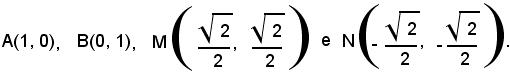
Si tralascia la considerazione dei seguenti casi particolari riportati in figura:
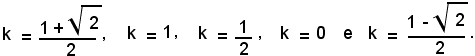
3)-Siano date le due curve di equazione:
Si determini la relazione che deve sussistere fra a e b affinchè le curve s'incontrino nel punto P1 del primo quadrante, avente per ascissa 2. Indicate con P2 e P3 le ulteriori intersezioni delle due curve e condotte per esse le tangenti alla C2, si denotino con T2 e T3 i punti di tali tangenti che hanno ordinate nulle e si calcolino le ascisse. Si determini infine a, in modo che la distanza fra T2 e T3 sia 4k(a - 2), essendo k un numero positivo dato.
Se si ritiene opportuno, si può calcolare l'area della regione comune alla striscia determinata dalle parallele condotte all'asse x e alla curva C.
La curva C1 rappresenta una parabola avente per asse l'asse y, il vertice V(0, a/2) e interseca l'asse x nei punti
La curva C2 rappresenta un'iperbole equilatera avente per asintoti gli assi cartesiani e disposta nel primo e terzo quadrante, b > 0.
Affinchè le curve s'incontrino nel punto P1, di ascissa 2 del primo quadrante, occorre che sia b > 0.
Le coordinate dei punti d'intersezione delle due curve sono date dalle soluzioni del sistema formato dalle equazioni di C1 e C2:
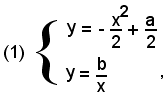
da cui si ricava, sostituendo il valore della y della prima equazione del sistema nella seconda,
Tale equazione ammette la radice x = 2, se:
4 - a + b = 0,
cioè
b = a - 4.
Affinchè P1 appartenga al primo quadrante, occorre, dunque, che:
cioè
Dopo aver osservato che dell'equazione (2) si conosce la radice x = 2 e la relazione tra a e b, ossia b = a - 4; applicando la regola di Ruffini all'equazione x3 - ax + 2a - 8 = 0, si ricava x3 - ax + 2a - 8 = (x - 2)(x2 + 2x + 4 - a), ossia:
Sostituendo tali valori nella prima equazione del sistema (1), y = (a - 4)x, si hanno i valori delle ordinate. Si hanno quindi le coordinate degli altri due punti P2 e P3, d'intersezione delle curve C1 e C2:


Le ascisse dei punti T2 e T3, intersezioni dell'asse x delle tangenti all'iperbole nei punti, rispettivamente, P2 e P3, si ricavano considerando che P2 e P3, punti di contatto delle tangenti, sono punti medi, rispettivamente, dei segmenti T2R e T3S e quindi anche le loro proiezioni suill'asse x, come anche sull'asse y, M e N sono punti medi dei segmenti OT2 e OT3. Si ha quindi:
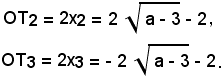
La distanza:
essa dev'essere
Elevando al quadrato, riducendo ed ordinando, si ottiene:
I valori di a soddisfacenti il nostro problema sono dati dalle soluzioni del sistema:
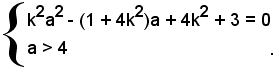
Tale sistema ammette l'unica soluzione a2 per
L'area della regione comune alla striscia determinata dalle rette y = y2 e y = y3 e dalla parabola, si ottiene come differenza dei segmenti parabolici P3VQ e UVP2, il cui valore è dato da:
Nota bene: