MIKY & GENNY
DISCUSSIONE DELLE EQUAZIONI PARAMETRICHE DI SECONDO GRADO ---> INDICE
Prima
di discutere le equazioni parametriche di secondo grado
mediante l'uso della parabola, si ricordano alcune proprietà di tale curva.
La parabola rappresentata dall'equazione:
y = ax2 + bx + c
ha il vertice nel punto V di coordinate
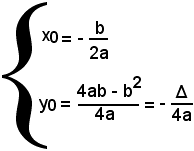
e la concavità rivolta verso l'alto o verso il basso, a seconda che sia, rispettivamente, a > 0 o a < 0.
Le coordinate degli eventuali punti d'intersezione della parabola con l'asse x sono date dalle soluzioni del sistema:
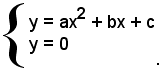
Le radici x1 e x2, con x1 < x2, dell'equazione risolvente ax2 + bx + c forniscono le ascisse degli eventuali punti d'intersezione della parabola con l'asse x.
Si è visto che:
-quando Δ = b2 - 4ac > 0, la parabola è tagliata dall'asse x in due punti reali e distinti;
-quando Δ = b2 - 4ac = 0, la parabola è tagliata dall'asse x in due punti reali e coincidenti, e l'asse x è tangente ad essa;
-quando Δ = b2 - 4ac < 0, la parabola non ha punti in comune con l'asse x.
Da quanto detto, rispetto agli assi coordinati, la parabola assume sei posizioni particolari.
1)-a > 0, la parabola ha la concavità rivolta verso l'alto.
Se Δ = b2 - 4ac > 0, la parabola taglia l'asse x in due punti reali e distinti di ascisse x1 e x2 e di ordinate nulle.
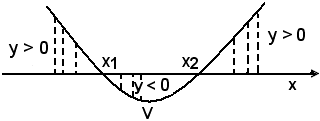
I punti della parabola di ordinate positive sono tutti e soltanto quelli le cui ascisse x sono minori di x1 o maggiori di x2, x < x1 o x > x2; i punti di ordinate negative sono tutti e soltanto quelli le cui ascisse x sono comprese tra x1 e x2, x1 < x < x2.
Se Δ = b2 - 4ac = 0, l'asse x è tangente alla parabola. I punti della curva hanno ordinate positive per qualsiasi valore di x, ad eccezione del punto, vertice, di ascissa x = -b/2a, la cui ordinata è nulla.
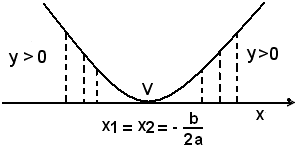
Se Δ = b2 - 4ac < 0, la parabola non taglia l'asse x.
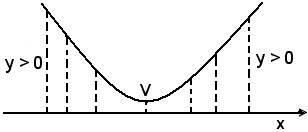
Tutti i punti della parabola hanno ordinate positive,
2)-a < 0, la parabola ha la concavità rivolta verso il basso.
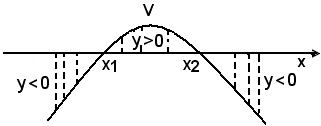
Se Δ = b2 - 4ac = 0, l'asse x è tangente alla parabola. Tutti i punti della parabola hanno ordinate negative, ad eccezione del punto, vertice, di ascissa x = -b/2a, la cui ordinata è nulla.
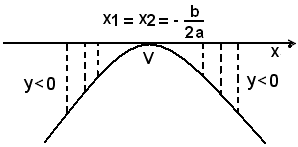
Se Δ = b2 - 4ac < 0, la parabola non taglia l'asse x.
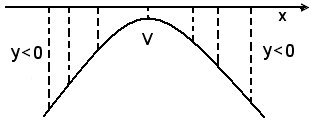
Tutti i punti della parabola hanno ordinate negative.
Applicazione della parabola alla risoluzione delle disequazioni di secondo grado
Per risolvere le disequazioni:
ax2 + bx + c > 0, ax2 + bx + c < 0,
si associa ad esse la parabola:
y = ax2 + bx + c.
Il problema è ricondotto a determinare per quali valori di x l'ordinata y della parabola è positiva o negativa.
Esempi
1)-Risolvere la disequazione:
x2 - 5x + 6 > 0.
Si associa ad essa la parabola y = x2 - 5x + 6. Poichè il coefficiente di x2 è positivo, ed il Δ = 25 - 24 = 1 > 0, la parabola ha la concavità verso l'alto e interseca l'asse x in due punti reali e distinti, le cui ascisse 2 e 3 sono radici dell'equazione x2 - 5x + 6 = 0.
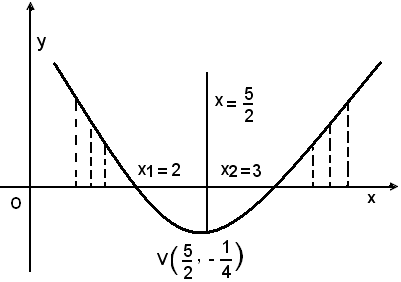
I punti della parabola aventi ordinate positive sono tutti e soltanto quelli le cui ascisse sono minori di 2 o maggiori di 3. Di conseguenza la disequazione x2 - 5x + 6 > 0 è soddisfatta dai soli valori di x esterni all'intervallo degli zeri del trinomio x2 - 5x + 6; ossia per x < 2 o x > 3.
Nota bene
Il discriminante e le radici dell'equazione ax2 + bx + c = 0 si dicono, rispettivamente, discriminante e zeri del trinomio ax2 + bx + c.
2)-Risolvere la disequazione:
-x2 + 7x - 6 > 0.
Si associa ad essa la parabola y = -x2 + 7x - 6; essa presenta concavità negativa rivolta verso il basso, essendo a = -1 e taglia l'asse x nei punti di ascisse 1 e 6 perchè Δ = 25 > 0.
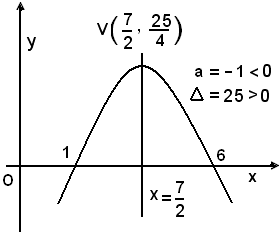
I punti della parabola aventi ordinate positive sono tutti e soltanto quelli le cui ascisse sono comprese fra 1 e 6. La disequazione data, dunque, è soddisfatta dai valori della x compresi nell'intervallo degli zeri del trinomio, ossia da 1 < x < 6.
3)-Risolvere la disequazione:
x2 + x + 1 < 0.
Si associa ad essa la parabola y = x2 + x + 1; essa presenta concavità positiva rivolta verso l'alto, essendo a = 1 e non taglia l'asse x perchè Δ = -3 < 0. Non esistono, quindi, punti della parabola aventi ordinate negative. La disequazione, pertanto, non ammette soluzioni, quindi è impossibile.
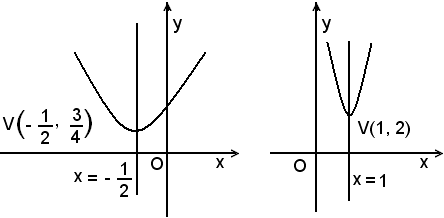
4)-Risolvere la disequazione:
x2 - 2x + 5 > 0.
Si associa ad essa la parabola y = x2 - 2x + 5; essa presenta concavità positiva rivolta verso l'alto, essendo a = 1 > 0 e non taglia l'asse x, perchè Δ = -4 < 0. Tutti i punti della parabola hanno ordinate positive; pertanto la disequazione è soddisfatta per qualsiasi valore di x.
Confronto delle radici di un'equazione di secondo grado a un'incognita con un numero reale dato
Sia data l'equazione ax2 + bx + c = 0, le cui radici siano reali, Δ = b2 - 4ac ≥ 0; si vuole confrontare tali radici con il numero reale α, cioè determinare la posizione di α rispetto a x1 e x2. Si indica con Σ la semisomma delle radici dell'equazione ax2 + bx + c = 0, ossia:
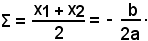
Si possono presentare i seguenti casi:
Δ > 0

Δ = 0
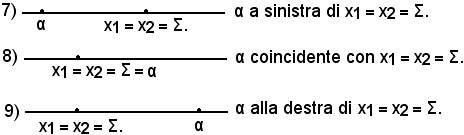
Per determinare le condizioni affinchè si verifichi uno dei casi suddetti, si pone f(x) = ax2 + bx + c e si associa all'equazione f(x) = ax2 + bx + c = 0 la parabola:
y = af(x) = a(ax2 + bx + c) = a2x2 + abx + ac = 0,
la quale, essendo a2 > 0, presenta sempre la concavità rivolta verso l'alto.
Nota bene
Si è considerata la parabola y = af(x) = a2x2 + abx + ac e non la parabola y = f(x) = ax2 + bx + c, perchè in tal modo si possono considerare solo tre grafici, a seconda del segno del discriminante.
Si indica ora con af(α) = a(aα2 + bα + c = 0) = a2α2 + abα + ac l'ordinata del punto della parabola di ascissa α.
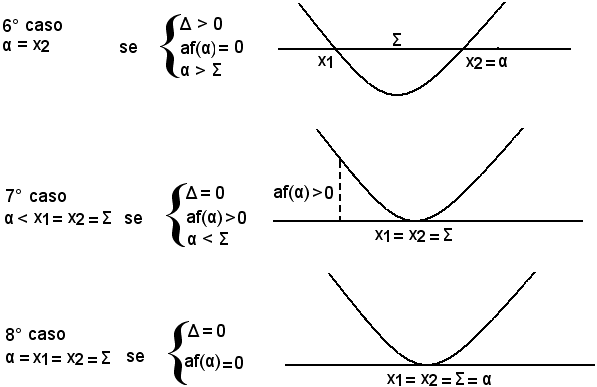
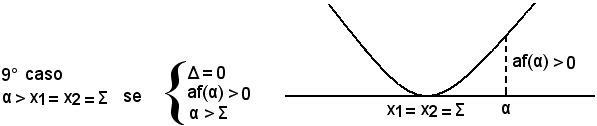
Se af(α) < 0, α è interno all'intervallo delle radici x1 e x2 dell'equazione f(x) = 0.
Se af(α) > 0, α è esterno all'intervallo delle radici ed è alla sinistra di x1, cioè α < x1 se α < Σ; a destra di x2, cioè α < x2 se α > Σ. Concludendo:
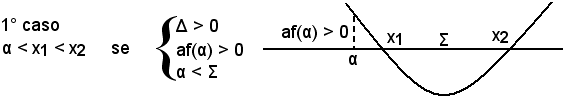
Ordinariamente il confronto fra α e Σ si effettua studiando il segno di α - Σ. E' evidente che se α - Σ < 0, risulta α < Σ, come anche se α - Σ > 0, risulta α > Σ.
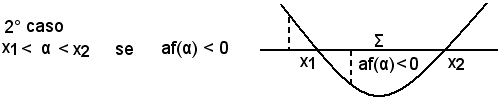
Se α è interno all'intervallo [x1, x2], la parabola deve tagliare l'asse x, ossia deve verificarsi Δ > 0.
Infatti, se fosse Δ = 0, la parabola risulterebbe tangente all'asse x; se fosse Δ < 0, la parabola non taglierebbe l'asse x.
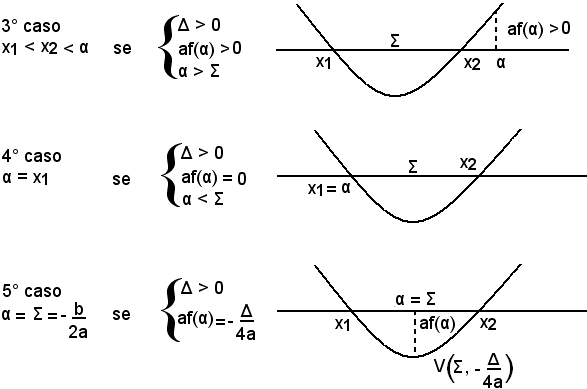
Esempi
1)-Confrontare le radici dell'equazione x2 - 5x + 6 = 0 con il numero 4.
Si pone f(x) = x2 - 5x + 6 = 0 e si associa all'equazione data la parabola y = af(x) = x2 - 5x + 6 la quale presenta concavità positiva, perchè a = 1, e taglia l'asse x in due punti reali e distinti, in quanto Δ > 0. Si calcola:
af(4) = 42 - 5·4 + 6 = 16 - 20 + 6 = 2 > 0,
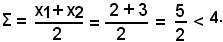
Si ha dunque:
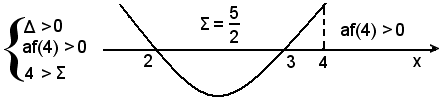
ossia α è esterno all'intervallo ed è maggiore di Σ, cioè
x1 < x2 < 4.
2)-Confrontare le radici dell'equazione x2 - (k - 1)x - 20 = 0 con il numero α = 2.
Si pone f(x) = x2 - (k - 1)x - 20, ove a = 1, Δ = k2 - 2k + 81 > 0 per qualsiasi valore di k, essendo il discriminante del trinomio in k, 4 - 324 = -320 < 0.
Si calcola:
af(2) = 4 - (k - 1)·2 - 20 = 4 - 2k + 2 - 20 = -2k - 14,
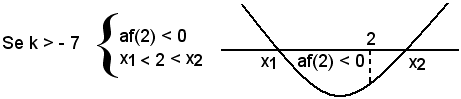
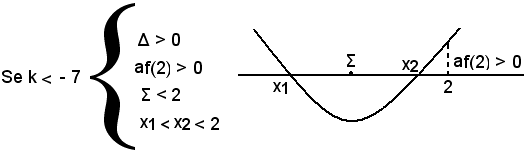
af(2) ≥ 0 per -2k - 14 ≥ 0; k + 7 ≤ 0; k ≤ -7,
af(2) ≤ 0 per -2k - 14 ≤ 0; k + 7 ≥ 0; k ≥ -7.
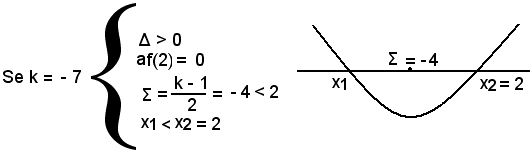
3)-Confrontare le radici dell'equazione (m - 3)x2 + 2(m - 1)x + m + 3 = 0 con il numero α = 1.
Si associa all'equazione:
f(x) = (m - 3)x2 + 2(m - 1)x + (m + 3) = 0
la parabola
af(x) = (m - 3)2x2 + 2(m - 1)(m + 3)x + m2 - 9;
essa presenta sempre concavità positiva essendo (m - 3)2 > 0, m ≠ 3. L'asse x è tangente o secante la parabola, a seconda che:
Δ = (m - 1)2 - m2+ 9 = m2 - 2m + 1 - m2+ 9 = 2m + 10 ≥ 0,
ossia
(4 - 2m)(m - 3) < 0,
cioè
m2 - 5m + 6 < 0;
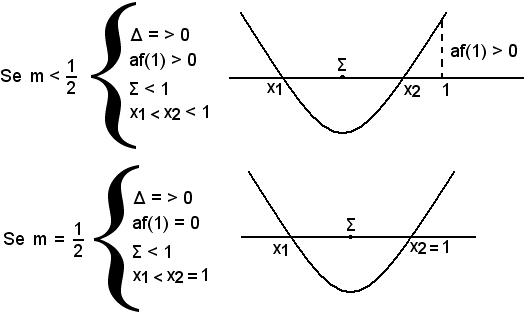
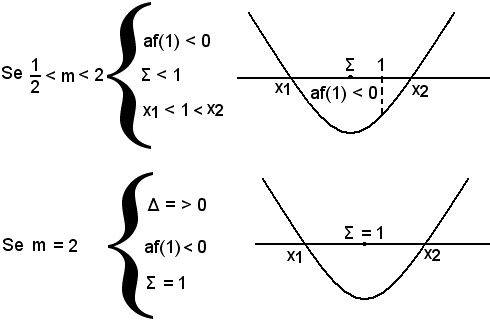
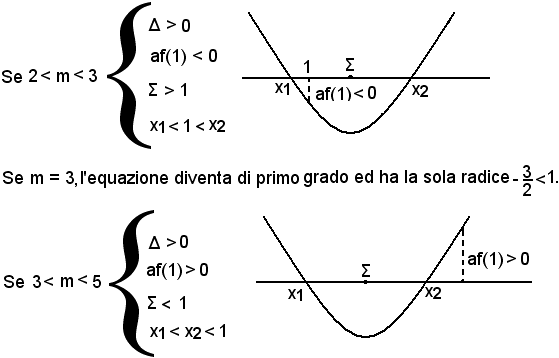
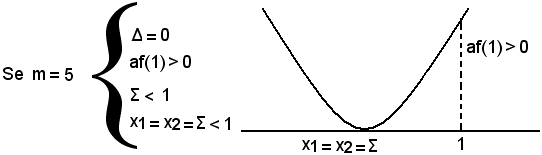
disequazione soddisfatta dai valori m < 2 e m > 3.
Si ordinano i valori particolari del parametro m, detti capisaldi della discussione, in ordine crescente:
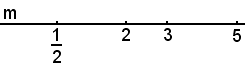
Confronto della radici di un'equazione di secondo grado ad una incognita con due numeri dati
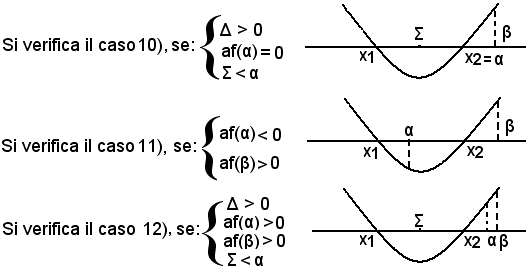
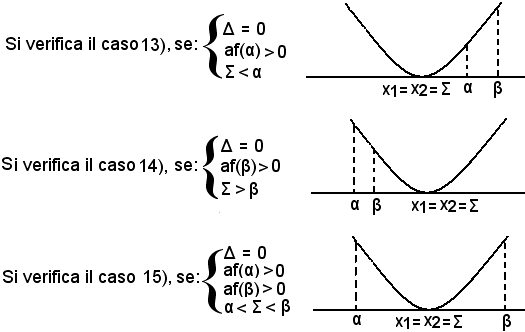
Si vogliono confrontare le radici dell'equazione f(x) = ax2 + bx + c = 0 con la coppia di numeri reali α e β, con α < β, cioè si vogliono determinare le posizioni di α e β rispetto all'intervallo [x1, x2]. Si possono presentare i seguenti casi:
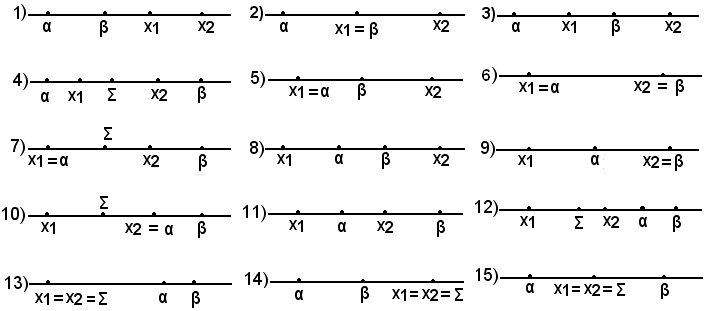
Per determinare le condizioni necessarie e sufficienti affinchè si verifichi uno dei casi suddetti, si associa all'equazione f(x) = ax2 + bx + c = 0 le ordinate dei punti della parabola, aventi rispettivamente ascisse α e β. I punti α e β sono esterni interni all'intervallo [x1, x2] a seconda che af(α) e af(β) siano rispettivamente positive o negative.
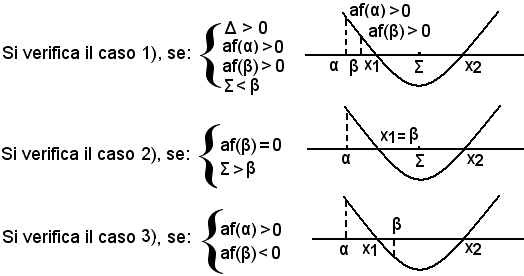
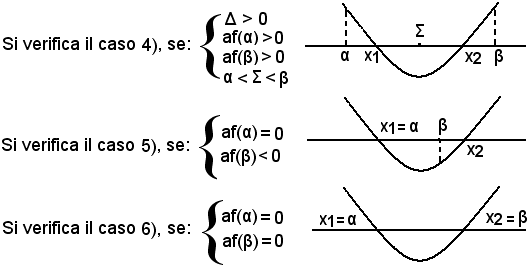
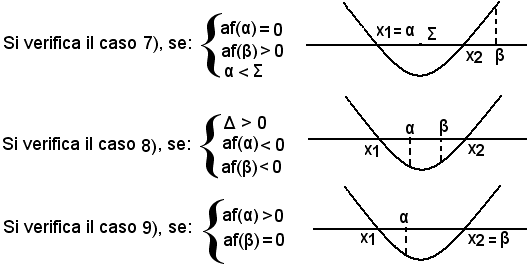
Esempi
1)-Confrontare le radici dell'equazione f(x) = 24x2 + 2x - 1 = 0, senza risolverla, con la coppia di numeri 1 e 2.
Si associa all'equazione f(x) = 24x2 + 2x - 1 = 0 la parabola:
y = af(x) = 242x2 + 48x - 24 = 0.
L'asse x taglia la parabola in due punti, poichè Δ/4 = 1 + 24 = 25 > 0. Le ordinate dei punti della parabola, di ascisse rispettivamente 1 e 2 sono date da:
af(1) = 242 + 48 - 24 = 24·25 > 0,
af(2) = 242·2 + 48·2 - 24 = 24·99 > 0,
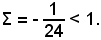
Si ha quindi:
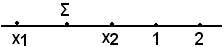
2)-Confrontare le radici dell'equazione x2 - (m - 1)x - m + 1 = 0 con la coppia di numeri -1 e 2.
All'equazione data si associa la parabola:
y = af(x) = x2 - (m - 1)x - m + 1.
L'asse x è tangente o secante a seconda che:
Δ = (m - 1)2 + 4m - 4 ≥ 0,
m2 + 2m - 3 ≥ 0,
ossia
per m < -3 o per m > 1.
Si calcolano i punti della parabola rispettivamente di ascisse -1 e 2 ed il Σ:
af(-1) = 1 + m - 1 - m + 1 = 1 > 0,
af(2) = 4 - 2m + 2 - m + 1 = - 3m + 7 > 0 per m < 7/3,
af(2) = 4 - 2m + 2 - m + 1 = - 3m + 7 = 0 per m = 7/3,
af(2) = 4 - 2m + 2 - m + 1 = - 3m + 7 < 0 per m > 7/3.
Essendo
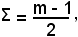
si ha:
Σ > -1 per m > -1,
Σ < 2 per m < 5.
Si ordinano i valori del parametro in ordine crescente, capisaldi della discussione e si considerano solo gl'intervalli parziali, in cui è suddiviso l'intervallo reale dei capisaldi, in cui Δ > 0.
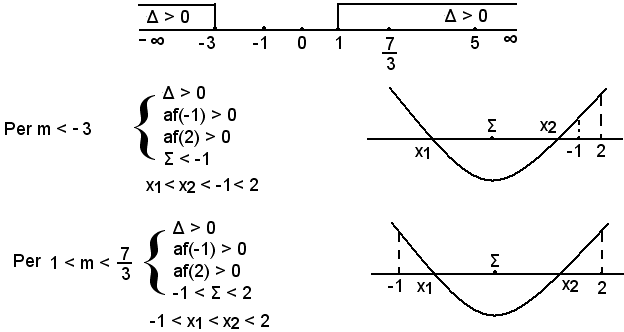
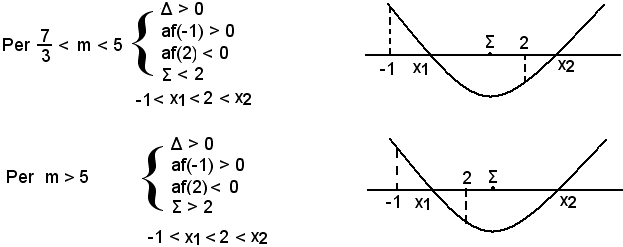
Casi particolari
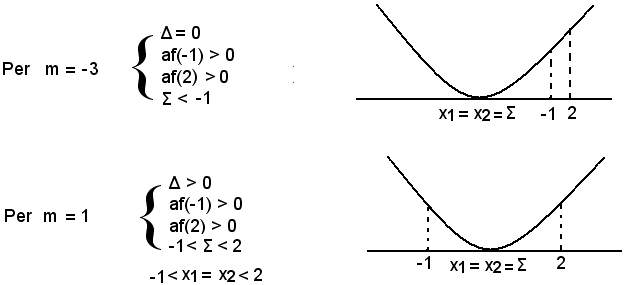
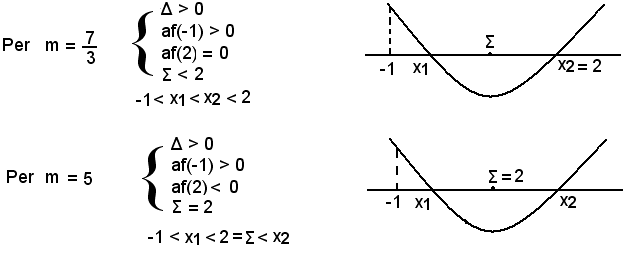
3)-Determinare per quali valori del parametro m l'equazione f(x) = (m - 1)x2 - (m + 2)x + m - 6 = 0 ha soluzioni comprese fra -1 e +1.
All'equazione data si associa la parabola:
y = af(x) = (m - 1)f(x),
che ha sempre la concavità positiva rivolta verso l'alto.L'asse x è secante o tangente alla parabola, cioè l'equazione ha radici reali, se:
Δ = (m + 2)2 - 4(m - 1)(m - 6) ≥ 0,
da cui
Δ ≥ 0 per 2/3 < m < 1.
Si calcolano le ordinate dei punti della parabola, di ascisse rispettivamente -1 e +1 e la posizione di Σ rispetto ad essi.
af(-1) = (m - 1)(3m - 5);
af(-1) ≥ 0 per m ≤ 1 o m ≥ 5/3,
af(-1) < 0 per 1 < m < 5/3.
af(1) = (m - 1)(m - 9);
af(1) ≥ 0 per m ≤ 1 o m ≥ 9,
af(1) < 0 per 1 < m < 9.
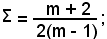
Σ > -1 per m < 0 o m > 1,
Σ < 1 per m < 1 o m > 4.
Dai risultati precedenti si ha la soluzione x1, se:
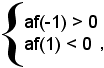
ossia se
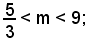
la soluzione x2, se
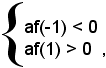
ossia se
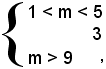
il sistema è impossibile, pertanto non si avrà mai la soluzione x2.
Si hanno le soluzioni x1 e x2, se:
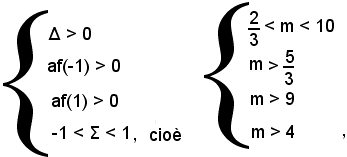
ossia se 9 < m < 10.
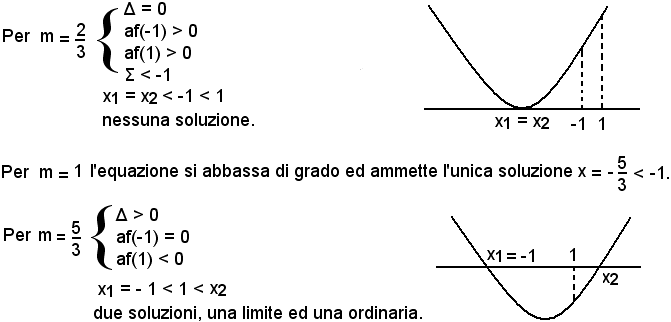
Casi particolari


La parabola rappresentata dall'equazione:
y = ax2 + bx + c
ha il vertice nel punto V di coordinate

e la concavità rivolta verso l'alto o verso il basso, a seconda che sia, rispettivamente, a > 0 o a < 0.
Le coordinate degli eventuali punti d'intersezione della parabola con l'asse x sono date dalle soluzioni del sistema:
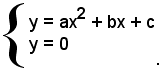
Le radici x1 e x2, con x1 < x2, dell'equazione risolvente ax2 + bx + c forniscono le ascisse degli eventuali punti d'intersezione della parabola con l'asse x.
Si è visto che:
-quando Δ = b2 - 4ac > 0, la parabola è tagliata dall'asse x in due punti reali e distinti;
-quando Δ = b2 - 4ac = 0, la parabola è tagliata dall'asse x in due punti reali e coincidenti, e l'asse x è tangente ad essa;
-quando Δ = b2 - 4ac < 0, la parabola non ha punti in comune con l'asse x.
Da quanto detto, rispetto agli assi coordinati, la parabola assume sei posizioni particolari.
1)-a > 0, la parabola ha la concavità rivolta verso l'alto.
Se Δ = b2 - 4ac > 0, la parabola taglia l'asse x in due punti reali e distinti di ascisse x1 e x2 e di ordinate nulle.

I punti della parabola di ordinate positive sono tutti e soltanto quelli le cui ascisse x sono minori di x1 o maggiori di x2, x < x1 o x > x2; i punti di ordinate negative sono tutti e soltanto quelli le cui ascisse x sono comprese tra x1 e x2, x1 < x < x2.
Se Δ = b2 - 4ac = 0, l'asse x è tangente alla parabola. I punti della curva hanno ordinate positive per qualsiasi valore di x, ad eccezione del punto, vertice, di ascissa x = -b/2a, la cui ordinata è nulla.

Se Δ = b2 - 4ac < 0, la parabola non taglia l'asse x.

Tutti i punti della parabola hanno ordinate positive,
2)-a < 0, la parabola ha la concavità rivolta verso il basso.
Se Δ = b2 - 4ac > 0, la parabola taglia l'asse x in due punti reali e distinti di ascisse x1 e x2 e di ordinate nulle. I punti della parabola di ordinate positive sono tutti e soltanto quelli le cui ascisse x sono comprese tra x1 e x2, x1 < x < x2; i punti di ordinate negative sono tutti e soltanto quelli le cui ascisse x sono minori di x1, o maggiori di x2, x < x1 o x > x2;

Se Δ = b2 - 4ac = 0, l'asse x è tangente alla parabola. Tutti i punti della parabola hanno ordinate negative, ad eccezione del punto, vertice, di ascissa x = -b/2a, la cui ordinata è nulla.

Se Δ = b2 - 4ac < 0, la parabola non taglia l'asse x.

Tutti i punti della parabola hanno ordinate negative.
Applicazione della parabola alla risoluzione delle disequazioni di secondo grado
Per risolvere le disequazioni:
ax2 + bx + c > 0, ax2 + bx + c < 0,
si associa ad esse la parabola:
y = ax2 + bx + c.
Il problema è ricondotto a determinare per quali valori di x l'ordinata y della parabola è positiva o negativa.
Esempi
1)-Risolvere la disequazione:
x2 - 5x + 6 > 0.
Si associa ad essa la parabola y = x2 - 5x + 6. Poichè il coefficiente di x2 è positivo, ed il Δ = 25 - 24 = 1 > 0, la parabola ha la concavità verso l'alto e interseca l'asse x in due punti reali e distinti, le cui ascisse 2 e 3 sono radici dell'equazione x2 - 5x + 6 = 0.

I punti della parabola aventi ordinate positive sono tutti e soltanto quelli le cui ascisse sono minori di 2 o maggiori di 3. Di conseguenza la disequazione x2 - 5x + 6 > 0 è soddisfatta dai soli valori di x esterni all'intervallo degli zeri del trinomio x2 - 5x + 6; ossia per x < 2 o x > 3.
Nota bene
Il discriminante e le radici dell'equazione ax2 + bx + c = 0 si dicono, rispettivamente, discriminante e zeri del trinomio ax2 + bx + c.
2)-Risolvere la disequazione:
-x2 + 7x - 6 > 0.
Si associa ad essa la parabola y = -x2 + 7x - 6; essa presenta concavità negativa rivolta verso il basso, essendo a = -1 e taglia l'asse x nei punti di ascisse 1 e 6 perchè Δ = 25 > 0.

I punti della parabola aventi ordinate positive sono tutti e soltanto quelli le cui ascisse sono comprese fra 1 e 6. La disequazione data, dunque, è soddisfatta dai valori della x compresi nell'intervallo degli zeri del trinomio, ossia da 1 < x < 6.
3)-Risolvere la disequazione:
Si associa ad essa la parabola y = x2 + x + 1; essa presenta concavità positiva rivolta verso l'alto, essendo a = 1 e non taglia l'asse x perchè Δ = -3 < 0. Non esistono, quindi, punti della parabola aventi ordinate negative. La disequazione, pertanto, non ammette soluzioni, quindi è impossibile.

4)-Risolvere la disequazione:
x2 - 2x + 5 > 0.
Si associa ad essa la parabola y = x2 - 2x + 5; essa presenta concavità positiva rivolta verso l'alto, essendo a = 1 > 0 e non taglia l'asse x, perchè Δ = -4 < 0. Tutti i punti della parabola hanno ordinate positive; pertanto la disequazione è soddisfatta per qualsiasi valore di x.
Confronto delle radici di un'equazione di secondo grado a un'incognita con un numero reale dato
Sia data l'equazione ax2 + bx + c = 0, le cui radici siano reali, Δ = b2 - 4ac ≥ 0; si vuole confrontare tali radici con il numero reale α, cioè determinare la posizione di α rispetto a x1 e x2. Si indica con Σ la semisomma delle radici dell'equazione ax2 + bx + c = 0, ossia:
Si possono presentare i seguenti casi:
Δ > 0

Δ = 0

Per determinare le condizioni affinchè si verifichi uno dei casi suddetti, si pone f(x) = ax2 + bx + c e si associa all'equazione f(x) = ax2 + bx + c = 0 la parabola:
y = af(x) = a(ax2 + bx + c) = a2x2 + abx + ac = 0,
la quale, essendo a2 > 0, presenta sempre la concavità rivolta verso l'alto.
Nota bene
Si è considerata la parabola y = af(x) = a2x2 + abx + ac e non la parabola y = f(x) = ax2 + bx + c, perchè in tal modo si possono considerare solo tre grafici, a seconda del segno del discriminante.
Si indica ora con af(α) = a(aα2 + bα + c = 0) = a2α2 + abα + ac l'ordinata del punto della parabola di ascissa α.
Se af(α) < 0, α è interno all'intervallo delle radici x1 e x2 dell'equazione f(x) = 0.
Se af(α) > 0, α è esterno all'intervallo delle radici ed è alla sinistra di x1, cioè α < x1 se α < Σ; a destra di x2, cioè α < x2 se α > Σ. Concludendo:
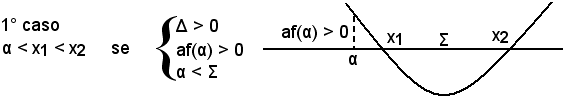
Ordinariamente il confronto fra α e Σ si effettua studiando il segno di α - Σ. E' evidente che se α - Σ < 0, risulta α < Σ, come anche se α - Σ > 0, risulta α > Σ.
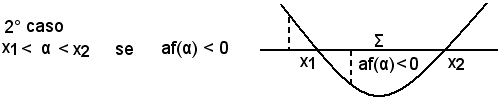
Infatti, se fosse Δ = 0, la parabola risulterebbe tangente all'asse x; se fosse Δ < 0, la parabola non taglierebbe l'asse x.



Esempi
1)-Confrontare le radici dell'equazione x2 - 5x + 6 = 0 con il numero 4.
Si pone f(x) = x2 - 5x + 6 = 0 e si associa all'equazione data la parabola y = af(x) = x2 - 5x + 6 la quale presenta concavità positiva, perchè a = 1, e taglia l'asse x in due punti reali e distinti, in quanto Δ > 0. Si calcola:
af(4) = 42 - 5·4 + 6 = 16 - 20 + 6 = 2 > 0,
Si ha dunque:

ossia α è esterno all'intervallo ed è maggiore di Σ, cioè
x1 < x2 < 4.
2)-Confrontare le radici dell'equazione x2 - (k - 1)x - 20 = 0 con il numero α = 2.
Si pone f(x) = x2 - (k - 1)x - 20, ove a = 1, Δ = k2 - 2k + 81 > 0 per qualsiasi valore di k, essendo il discriminante del trinomio in k, 4 - 324 = -320 < 0.
Si calcola:
af(2) = 4 - (k - 1)·2 - 20 = 4 - 2k + 2 - 20 = -2k - 14,
af(2) ≥ 0 per -2k - 14 ≥ 0; k + 7 ≤ 0; k ≤ -7,
af(2) ≤ 0 per -2k - 14 ≤ 0; k + 7 ≥ 0; k ≥ -7.

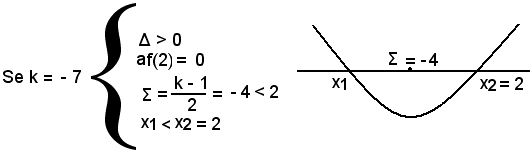

3)-Confrontare le radici dell'equazione (m - 3)x2 + 2(m - 1)x + m + 3 = 0 con il numero α = 1.
Si associa all'equazione:
f(x) = (m - 3)x2 + 2(m - 1)x + (m + 3) = 0
la parabola
af(x) = (m - 3)2x2 + 2(m - 1)(m + 3)x + m2 - 9;
essa presenta sempre concavità positiva essendo (m - 3)2 > 0, m ≠ 3. L'asse x è tangente o secante la parabola, a seconda che:
Δ = (m - 1)2 - m2+ 9 = m2 - 2m + 1 - m2+ 9 = 2m + 10 ≥ 0,
ossia per m ≤
-5.
Si osserva ora per quali valori del parametro m l'ordinata del punto della parabola di ascissa 1 è positiva, nulla o negativa:
af(1) = (m - 3)2 + 2(m - 1)(m + 3) + m2 - 9 = m2 - 6m + 9 + 2m2 - 8m + 6 + m2 - 9 =
4m2 - 14m + 6 > 0,
af(1) = (m - 3)2 + 2(m - 1)(m + 3) + m2 - 9 = m2 - 6m + 9 + 2m2 - 8m + 6 + m2 - 9 =
4m2 - 14m + 6 = 0,
af(1) = (m - 3)2 + 2(m - 1)(m + 3) + m2 - 9 = m2 - 6m + 9 + 2m2 - 8m + 6 + m2 - 9 =
4m2 - 14m + 6 < 0,
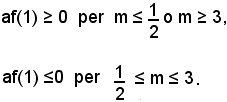
Inoltre, essendo:
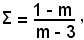
si ha
Σ < 1 per m < 2 o m > 3.
Infatti, si ha Σ - 1 < 0, cioè:
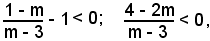
Si osserva ora per quali valori del parametro m l'ordinata del punto della parabola di ascissa 1 è positiva, nulla o negativa:
af(1) = (m - 3)2 + 2(m - 1)(m + 3) + m2 - 9 = m2 - 6m + 9 + 2m2 - 8m + 6 + m2 - 9 =
4m2 - 14m + 6 > 0,
af(1) = (m - 3)2 + 2(m - 1)(m + 3) + m2 - 9 = m2 - 6m + 9 + 2m2 - 8m + 6 + m2 - 9 =
4m2 - 14m + 6 = 0,
af(1) = (m - 3)2 + 2(m - 1)(m + 3) + m2 - 9 = m2 - 6m + 9 + 2m2 - 8m + 6 + m2 - 9 =
4m2 - 14m + 6 < 0,
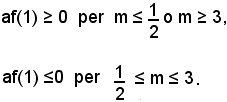
Inoltre, essendo:
si ha
Σ < 1 per m < 2 o m > 3.
Infatti, si ha Σ - 1 < 0, cioè:
ossia
(4 - 2m)(m - 3) < 0,
cioè
m2 - 5m + 6 < 0;
disequazione soddisfatta dai valori m < 2 e m > 3.
Si ordinano i valori particolari del parametro m, detti capisaldi della discussione, in ordine crescente:
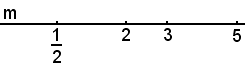




Confronto della radici di un'equazione di secondo grado ad una incognita con due numeri dati
Si vogliono confrontare le radici dell'equazione f(x) = ax2 + bx + c = 0 con la coppia di numeri reali α e β, con α < β, cioè si vogliono determinare le posizioni di α e β rispetto all'intervallo [x1, x2]. Si possono presentare i seguenti casi:
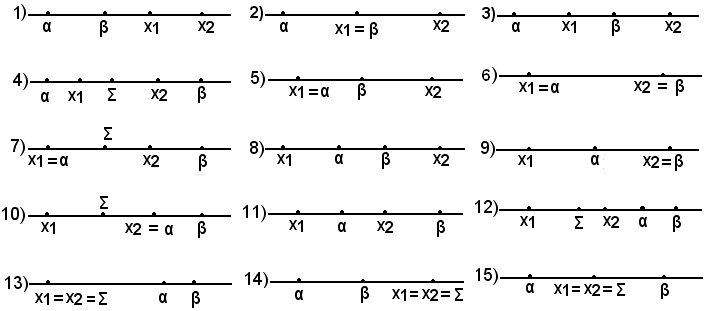
Per determinare le condizioni necessarie e sufficienti affinchè si verifichi uno dei casi suddetti, si associa all'equazione f(x) = ax2 + bx + c = 0 le ordinate dei punti della parabola, aventi rispettivamente ascisse α e β. I punti α e β sono esterni interni all'intervallo [x1, x2] a seconda che af(α) e af(β) siano rispettivamente positive o negative.
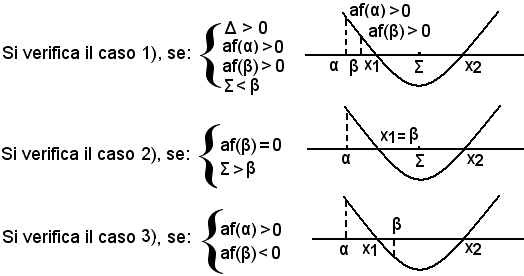
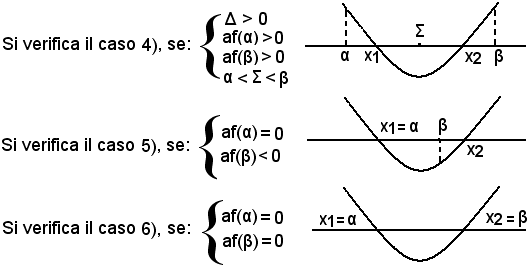
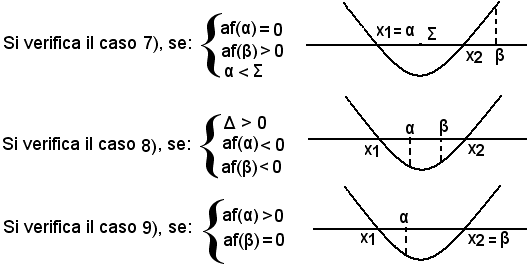


Esempi
1)-Confrontare le radici dell'equazione f(x) = 24x2 + 2x - 1 = 0, senza risolverla, con la coppia di numeri 1 e 2.
Si associa all'equazione f(x) = 24x2 + 2x - 1 = 0 la parabola:
L'asse x taglia la parabola in due punti, poichè Δ/4 = 1 + 24 = 25 > 0. Le ordinate dei punti della parabola, di ascisse rispettivamente 1 e 2 sono date da:
af(2) = 242·2 + 48·2 - 24 = 24·99 > 0,
Si ha quindi:
2)-Confrontare le radici dell'equazione x2 - (m - 1)x - m + 1 = 0 con la coppia di numeri -1 e 2.
All'equazione data si associa la parabola:
y = af(x) = x2 - (m - 1)x - m + 1.
L'asse x è tangente o secante a seconda che:
Δ = (m - 1)2 + 4m - 4 ≥ 0,
da cui
m2 + 2m - 3 ≥ 0,
ossia
per m < -3 o per m > 1.
Si calcolano i punti della parabola rispettivamente di ascisse -1 e 2 ed il Σ:
af(-1) = 1 + m - 1 - m + 1 = 1 > 0,
af(2) = 4 - 2m + 2 - m + 1 = - 3m + 7 > 0 per m < 7/3,
af(2) = 4 - 2m + 2 - m + 1 = - 3m + 7 = 0 per m = 7/3,
af(2) = 4 - 2m + 2 - m + 1 = - 3m + 7 < 0 per m > 7/3.
Essendo
si ha:
Σ > -1 per m > -1,
Σ < 2 per m < 5.
Si ordinano i valori del parametro in ordine crescente, capisaldi della discussione e si considerano solo gl'intervalli parziali, in cui è suddiviso l'intervallo reale dei capisaldi, in cui Δ > 0.

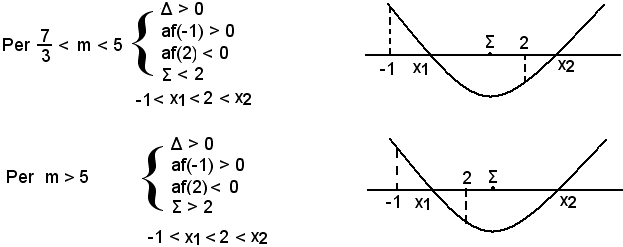
Casi particolari
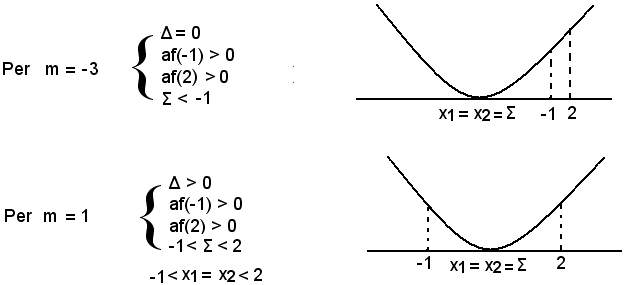
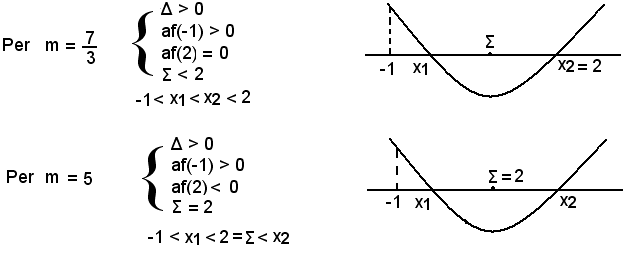
3)-Determinare per quali valori del parametro m l'equazione f(x) = (m - 1)x2 - (m + 2)x + m - 6 = 0 ha soluzioni comprese fra -1 e +1.
All'equazione data si associa la parabola:
y = af(x) = (m - 1)f(x),
che ha sempre la concavità positiva rivolta verso l'alto.
da cui
Δ ≥ 0 per 2/3 < m < 1.
Si calcolano le ordinate dei punti della parabola, di ascisse rispettivamente -1 e +1 e la posizione di Σ rispetto ad essi.
af(-1) = (m - 1)(3m - 5);
af(-1) ≥ 0 per m ≤ 1 o m ≥ 5/3,
af(-1) < 0 per 1 < m < 5/3.
af(1) = (m - 1)(m - 9);
af(1) ≥ 0 per m ≤ 1 o m ≥ 9,
af(1) < 0 per 1 < m < 9.
Σ > -1 per m < 0 o m > 1,
Dai risultati precedenti si ha la soluzione x1, se:
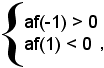
ossia se
la soluzione x2, se
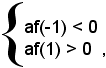
ossia se
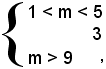
il sistema è impossibile, pertanto non si avrà mai la soluzione x2.
Si hanno le soluzioni x1 e x2, se:

ossia se 9 < m < 10.
Casi particolari


