MIKY & GENNY
APPLICAZIONI NUMERICHE E ALGEBRICHE ALLA GEOMETRIA ---> INDICE
La
teoria della misura, mediante la sostituzione delle grandezze con le
loro misure, permette di trasformare relazioni geometriche di
uguaglianza e di disuguaglianza in altrettante relazioni algebriche.
Tale trasformazione è molto utile, perchè permette
l'applicazione dell'algebra alla geometria:
1)-nella dimostrazione dei teoremi,
2)-nella risoluzione dei problemi geometrici.
1)-nella dimostrazione dei teoremi,
2)-nella risoluzione dei problemi geometrici.
La dimostrazione dei teoremi geometrici può, in alcuni casi, essere semplificata con l'ausilio dell'algebra.
Ad esempio, se a, b rappresentano le misure di segmenti, le identità:
(a + b)2 = a2 + b2+ 2ab
(a - b)2 = a2 + b2- 2ab
esprimono teoremi di geometria; precisamente:
1)-il quadrato costruito sulla somma di due segmenti equivale alla somma dei quadrati costruiti su questi, aumentata del doppio del loro rettangolo;
2)-il quadrato costruito sulla differenza di due segmenti equivale alla somma dei quadrati costruiti su questi, diminuita del doppio del loro rettangolo.
Le applicazioni numeriche e algebriche alla geometria sono molto utili per la risoluzione dei problemi.
Applicazioni al teorema di Pitagora
Il teorema di Pitagora esprime l'equivalenza fra il quadrato costruito sull'ipotenusa e la somma dei quadrati costruiti sui cateti. Quindi, se si indica con a la misura dell'ipotenusa e con b, c le misure dei cateti, essendo a2, b2, c2 le aree di tali quadrati, si ha la relazione:
a2 = b2 + c2,
che traduce la relazione fra grandezze geometriche in una relazione fra le rispettive misure, quindi fra numeri.
Ad esempio, se a, b rappresentano le misure di segmenti, le identità:
(a + b)2 = a2 + b2+ 2ab
(a - b)2 = a2 + b2- 2ab
esprimono teoremi di geometria; precisamente:
1)-il quadrato costruito sulla somma di due segmenti equivale alla somma dei quadrati costruiti su questi, aumentata del doppio del loro rettangolo;
2)-il quadrato costruito sulla differenza di due segmenti equivale alla somma dei quadrati costruiti su questi, diminuita del doppio del loro rettangolo.
Le applicazioni numeriche e algebriche alla geometria sono molto utili per la risoluzione dei problemi.
Applicazioni al teorema di Pitagora
Il teorema di Pitagora esprime l'equivalenza fra il quadrato costruito sull'ipotenusa e la somma dei quadrati costruiti sui cateti. Quindi, se si indica con a la misura dell'ipotenusa e con b, c le misure dei cateti, essendo a2, b2, c2 le aree di tali quadrati, si ha la relazione:
a2 = b2 + c2,
che traduce la relazione fra grandezze geometriche in una relazione fra le rispettive misure, quindi fra numeri.

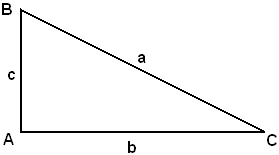
Applicazioni al triangolo rettangolo
Indicando con a la misura dell'ipotenusa e con b, c le misure dei cateti, dalla relazione fondamentale:
(1) a2 = b2 + c2,
si ricavano:
(2) b2 = a2 - c2,
(3) c2 = a2 - b2,
estraendo la radice quadrata da ambo i membri di 1), 2), 3), si ha:
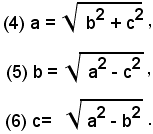
La (4) esprime che l'ipotenusa di un triangolo rettangolo si ottiene estraendo la radice quadrata della somma dei quadrati dei cateti.
Le (5) e (6) esprimono che un cateto di un triangolo rettangolo si ottiene estraendo la radice quadrata della differenza fra il quadrato dell'ipotenusa e il quadrato dell'altro cateto.
Applicazioni al rettangolo
Un rettangolo è diviso dalla sua diagonale in due triangoli rettangoli uguali, in ognuno di essi i cateti sono i lati e l'ipotenusa è la diagonale.
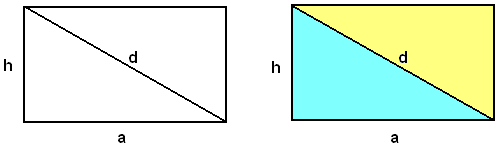
Perciò, se si indicano con a, b le dimensioni del rettangolo e con d la misura della diagonale, si hanno le formule;
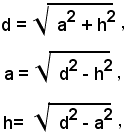
che permettono di ricavare la misura della diagonale quando sono noti i lati, oppure uno dei lati quando si conosce la diagonale e l'altro lato.
Applicazioni al quadrato
Indicando con l il lato di un quadrato e con d la misura della diagonale, per il teorema di Pitagora, si ha:
d2 = l2 + l2 ,
ossia
ed estraendo la radice quadrata da ambo i membri, si ricava:
cioè (1)
pertanto si ha la seguente regola:
-la diagonale di un quadrato si ottiene moltiplicando il lato per
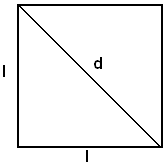
Dalla (1) si ricava:
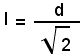
ovvero, moltiplicando ambo i termini per
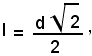
ossia il lato di un un quadrato si ottiene moltiplicando metà diagonale per
Applicazioni al triangolo isoscele
L'altezza divide il triangolo isoscele in due triangoli rettangoli uguali, ciascuno dei quali ha come cateti l'altezza e metà della base, e come ipotenusa il lato.
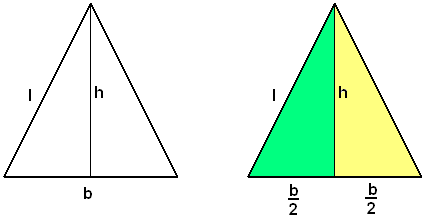
Indicando con h l'altezza, con b la base e con l il lato, si hanno le seguenti formule:
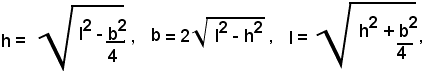
che permettono di calcolare l'altezza, la base e il lato, noti due di questi elementi.
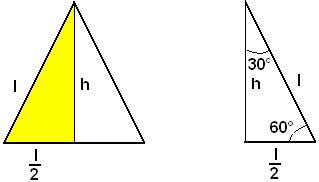
Applicazioni al triangolo equilatero
Uno dei due triangoli rettangoli in cui un'altezza divide un triangolo equilatero ha come ipotenusa il lato e come cateti l'altezza e la metà del lato.
Quindi, indicando con l il lato, e con h l'altezza, si ha:
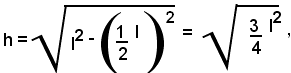
ossia (1)
da cui si ricava la seguente regola:
-l'altezza di un triangolo equilatero si ottiene moltiplicando metà del lato per
inversamente, dalla formula (1) si ricava:
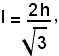
moltiplicando ambo i termini della frazione al secondo membro per
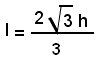
e questa formula dà il lato del triangolo equilatero conoscendo l'altezza.
Per l'area S, si ha:
e sostituendo ad h il valore trovato in precedenza, risulta
Quindi, la formula:
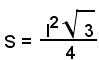
permette di calcolare l'area del triangolo equilatero conoscendo il lato.
Un triangolo rettangolo che ha un angolo acuto di 60° e l'altro di conseguenza di 30°, si può considerare come uno dei triangoli rettangoli che si ottiene tracciando l'altezza in un triangolo equilatero e quindi torna utile l'applicazione delle formule precedenti. Quindi:
-se un triangolo rettangolo ha un angolo acuto di 30°, e l'altro di 60°, il cateto opposto all'angolo di 30° è uguale alla metà dell'ipotenusa; l'altro cateto è uguale a metà ipotenusa moltiplicata per
Teorema di Pitagora generalizzato - Il quadrato costruito su un lato qualsiasi di un triangolo è equivalente alla somma dei quadrati degli altri due lati, ovvero a questa somma aumentata o diminuita del doppio rettangolo di uno di questi lati per la proiezione dell'altro su di esso, a seconda che il lato che si considera è opposto ad un angolo retto, ottuso o acuto.
Sia ABC un triangolo qualsiasi;
-se l'angolo in A è retto, il teorema è noto;
-se l'angolo in A è ottuso o acuto, si pone:
Si ha:

Considerando contemporaneamente entrambi i casi e applicando il teorema di Pitagora al triangolo CBD, si ha:
BC2 = BD2 + CD2
e sostituendo le misure,
a2 = (c ± m)2+ h2
e sostituendo le misure,
a2 = (c ± m)2+ h2
e quindi
a2 = c2 ± 2cm + m2 + h2.
Siccome
m2 + h2 = b2,
si ha
a2 = b2 + c2 ± 2cm.
si ha
a2 = b2 + c2 ± 2cm.
Altezze, mediane e bisettrici di un triangolo
Problema - Conoscendo i lati di un triangolo, determinare le altezze.
Sia ABC un triangolo qualsiasi, si pone:
Poichè degli angoli di un triangolo due sono almeno acuti, sia
Dopo aver tracciato l'altezza AD, e posto:
per il teorema di Pitagora generalizzato, si ha:
c2 = a2 + b2 -2ab',
da cui
Inoltre, dal triangolo ABC, si ha:
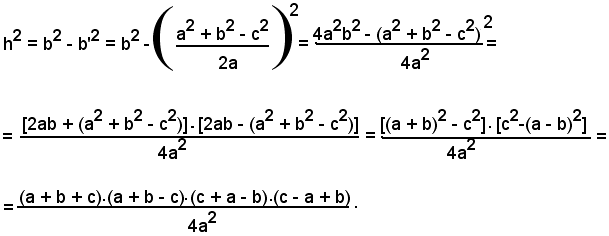
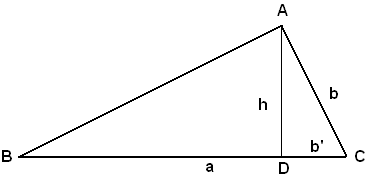
Indicando con 2p la misura del perimetro, cioè posto:
a + b + c = 2p,
sottraendo 2a da ambo i membri, si ricava
- a + b + c = 2(p -a)
e analogamente
a - b + c = 2(p -b),
a + b - c = 2(p - c).
Quindi la formula precedente si può scrivere:
da cui
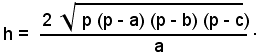
Formula di Erone
Indicando con S l'area del triangolo, si ha:
cioè
Questa formula, che prende il nome di formula di Erone, permette di calcolare l'area di un triangolo conoscendo le misure dei lati.
Formule analoghe si hanno per le mediane e le bisettrici relative agli altri due lati.
Raggi dei cerchi inscritti, circoscritti ed exinscritti in un triangolo
Si risolvono i seguenti problemi:
1)-dati i lati di un triangolo, trovare il raggio del cerchio inscritto.
Considerato il triangolo ABC, O il centro del cerchio inscritto, si congiunge O con A, con B, con C e indicate con S l'area del triangolo ABC, con SBCO l'area del triangolo BCO, con SACO l'area del triangolo ACO e con SABO l'area del triangolo ABO, si ha:
S = SBCO + SACO + SABO.
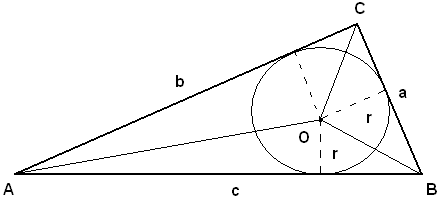
Si nota che i tre triangoli hanno la stessa altezza, che è il raggio del cerchio inscritto, quindi, passando alle misure e indicando con a, b, c le misure dei lati, con r la misura del raggio del cerchio inscritto, si ha:
cioè
e ponendo
a + b + c = 2p,
si ottiene
S = rp,
da cui
Con procedimento analogo al precedente, indicando con ra il raggio del cerchio tangente al lato a ed ai prolungamenti degli altro due lati, exinscritto relativo al lato a, si perviene alla formula:
Formule analoghe si hanno per i raggi di cerchi exinscritti relativi agli altri due lati.
2)-dati i lati di un triangolo, trovare il raggio del cerchio circoscritto.
Sia dato il triangolo ABC, O il centro della circonferenza circoscritta e AD l'altezza relativa al lato BC. Si congiunge A con O e si prolunga fino ad incontrare in E la circonferenza circoscritta. I due triangoli rettangoli ACE, ADB sono simili perchè hanno gli angoli in B ed in E uguali, insistendo sullo stesso arco
Si ha dunque:
AC : AD = AE : AB
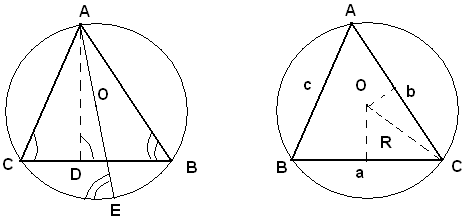
Indicando con a, b, c le misure dei lati BC, AC, AB, con R il raggio del cerchio circoscitto e con h l'altezza relativa a BC, dalla proporzione precedente si ricava:
b : h = 2R : c,
da cui
bc = 2R.
Moltiplicando ambo i membri della relazione precedente per a/4, si ha:
ossia, indicando con S l'area del triangolo
da cui
Lati di poligoni regolari inscritti in una circonferenza
1)-Determinare la misura del lato del triangolo equilatero inscritto in una circonferenza di cui si conosce la misura del raggio.
Sia ABC il triangolo equilatero inscritto nella circonferenza di centro O. Si pone:
AB = l, OA = r,
si traccia l'altezza AD e la si prolunga fino ad incontrare in E la circonferenza; inoltre si congiungono O ed E con B e con C, pertanto risulta:
perchè il quadrilatero OBEC è un rombo, in quanto BE, EC, lati dell'esagono regolare inscritto, sono uguali al raggio.
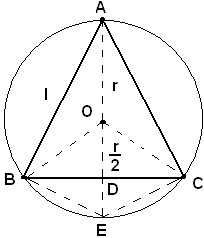
Applicando il teorema di Pitagora al triangolo OBD, si ha:
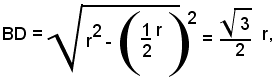
ed essendo
risulta
Nota bene
L'altezza
di un triangolo equilatero inscritto in una circonferenza è
uguale ai 3/2 del raggio; il centro della circonferenza la divide in
due parti, di cui quella che contiene il vertice è uguale al
raggio, l'altra è la metà del raggio stesso.
2)-Determinare la misura del lato di un quadrato inscritto in una circonferenza di cui si conosce la misura del raggio.
Sia ABCD il quadrato inscritto nella circonferenza di centro O. Si pone:
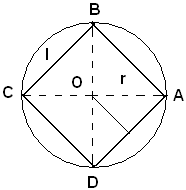
Dal triangolo rettangolo AOB si ricava:
q(AB) = q (AO) + q (OB)
e passando alle misure, si ha
l2 = r2 + r2
e successivamente
l2 = 2r2,
da cui
Nota bene
La distanza dal centro del cerchio dal lato del quadrato inscritto è uguale alla metà del lato stesso.
3)-Determinare la misura del lato dell'esagono regolare inscritto in una circonferenza di cui si conosce la misura del raggio.
Il lato dell'esagono regolare è uguale al raggio, quindi si ha;
l = r.
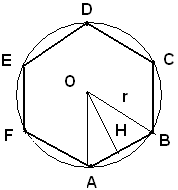
Nota bene
La distanza dal centro del cerchio di uno dei lati dell'esagono regolare inscritto, ossia l'apotema dell'esagono è uguale all'altezza di uno dei triangoli equilateri che si ottengono unendo il centro con gli estremi del lato stesso, essa è data da:
Risoluzione dei problemi geometrici mediante le applicazioni numeriche o algebriche
L'applicazione della misura per la risoluzione dei problemi di geometria consente la determinazione delle misure di certe grandezze geometriche, e quindi delle grandezze stesse, partendo dalle misure di altre grandezze note, o dati del problema.
Le misure delle grandezze possono essere date mediante numeri, e i problemi sono numerici, o possono essere indicate con lettere, e i problemi sono letterali.
Per la risoluzione dei problemi sia numerici che letterali, alcune volte, basta eseguire successive operazioni partendo dai dati, di regola le quattro operazioni fondamentali con l'aggiunta di estrazioni di radici; altre volte, occorre invece aggiungere fra i dati la misura di una grandezza incognita, indicandola, come si usa generalmente, con x.
Fra i dati e la x si può impostare un'equazione la cui risoluzione può condurre alla determinazione di x, e quindi alla grandezza corrispondente. Altre volte può essere conveniente assumere come note, invece di una, più grandezze incognite, pervenendo così ad un sistema di equazioni.
Per la risoluzione dei problemi geometrici con l'ausilio della misura, è utile indicare alcune direttive allo scopo di facilitare la scelta della via da seguire e di dare ordine e chiarezza all'esposizione.
1)-Si disegna la figura.
Se il problema è numerico, è opportuno che il disegno sia possibilmente in scala; in ogni caso è necessario che sia nitido e che si avvicini a quanto è indicato nell'enunciato. Si deve evitare di disegnare figure particolari, a meno che non sia richiesto dal problema; se si tratta di un triangolo qualsiasi, non si deve disegnare un triangolo isoscele, nè un triangolo equilatero o un triangolo rettangolo, ecc; se si deve tracciare una semiretta qualsiasi dentro un angolo a partire dal vertice, non si deve disegnare la bisettrice, ecc.
Una figura ben disegnata aiuta a trovare la risoluzione del problema e, se in scala, permette di controllare i risultati; viceversa una figura non conforme all'enunciato o poco chiara, può indurre ad errori.
2)-Si mettono in evidenza i dati.
La conoscenza e la posizione delle grandezze date sulla figura, in relazione a quelle che si devono trovare, sono indispensabili perchè forniscono orientamente sulla via da seguire.
3)-Si determinano le grandezze incognite.
Tali grandezze si calcolano, se è possibile direttamente, partendo dai dati, oppure s'imposta un'equazione, o il sistema di equazioni, fra i dati e l'incognita, o più incognite, opportunamente scelte.
In tal caso, si dice grado di un problema, il grado dell'equazione o del sistema di equazioni cui si perviene. Tanto se si deve procedere al calcolo diretto, delle grandezze incognite, quanto se occorre impostare equazioni, bisogna tener presente le relazioni che si traggono direttamente dall'enunciato e dai teoremi che si possono applicare alla figura.
Questi teoremi generalmente riguardano i triangoli; perciò, si deve osservare se nella figura esistono triangoli, oppure se è possibile tracciare opportunamnente dei segmenti ausiliari.
Dai triangoli uguali si possono trarre relazioni di uguaglianza fra i loro elementi.
Dai triangoli simili si possono dedurre proporzionifra i lati omologhi.
Ai triangoli rettangoli si possono applicare il teorema di Pitagora e i due teoremi di Euclide.
Conviene ricordare pure le principali proprietà del cerchio, il teorema di Talete e alcune formule importanti trattate.
4)-Si controllano i risultati e si cercano le condizioni per la possibilità del problema.
Si controlla se il problema è numerico o ammette soluzioni o non ne ammette affatto.
Quindi, le soluzioni, se esitono si accettano senz'altro; conviene tuttavia fare qualche verifica per il controllo dei calcoli.
Tale controllo può essere anche effettuato sulla figura; occorre naturalmente che essa sia disegnata in scala, per cui, se con dati del problema era apparso impossibile o poco agevole procedere alla costruzione esatta, si deve rifare la figura, approfittando dei valori trovati nel corso della riusoluzione.
Se invece il problema è letterale, può darsi che esso non ammetta soluzione solo per alcuni valori di quelli assegnati. Pervenuti quindi ad un risultato letterale, prima di accettarlo, occorre vedere quali condizioni fra quelle date devono essere soddisfatte affinchè il problema sia possibile.
Tali condizioni si possono desumere discutendo la soluzione trovata.
Se un problema è di primo grado, le soluzioni in generale devono essere positive; sono da accettare anche, in taluni casi, soluzioni negative previa opportuna interpretazione.
Se il problema è di secondo grado, le soluzioni devono essere innanzitutto reali; ciò esclude che fra le operazioni necessarie, per ricavarle si possono estrarre radici quadrate di numeri negativi. Le condizioni di realtà escludono quindi che le operazioni sotto il segno di radice quadrate diano luogo a numeri negativi.
Notevole interesse possono presentare nei problemi letterali certe soluzioni per valori particolari di quelli dati; è bene metterle in evidenza e trattarle a parte.
Con le indicazioni date, si risolvono ora alcuni problemi.
Problema 1) - L'altezza di un triangolo isoscele è cm 48, il raggio del cerchio inscritto cm 18; calcolare il perimetro del triangolo.
Sia dato il triangolo ABC e O il centro del cerchio inscritto. I dati sono quindi:
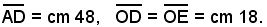
Si ha:
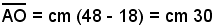
e
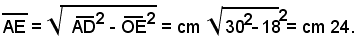
Dai triangoli simili AOE ed ACD, si ricava la proporzione:
DC : OE =AD : AE,
ossia
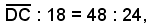
da cui
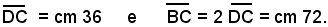
Conviene ricordare pure le principali proprietà del cerchio, il teorema di Talete e alcune formule importanti trattate.
4)-Si controllano i risultati e si cercano le condizioni per la possibilità del problema.
Si controlla se il problema è numerico o ammette soluzioni o non ne ammette affatto.
Quindi, le soluzioni, se esitono si accettano senz'altro; conviene tuttavia fare qualche verifica per il controllo dei calcoli.
Tale controllo può essere anche effettuato sulla figura; occorre naturalmente che essa sia disegnata in scala, per cui, se con dati del problema era apparso impossibile o poco agevole procedere alla costruzione esatta, si deve rifare la figura, approfittando dei valori trovati nel corso della riusoluzione.
Se invece il problema è letterale, può darsi che esso non ammetta soluzione solo per alcuni valori di quelli assegnati. Pervenuti quindi ad un risultato letterale, prima di accettarlo, occorre vedere quali condizioni fra quelle date devono essere soddisfatte affinchè il problema sia possibile.
Tali condizioni si possono desumere discutendo la soluzione trovata.
Se un problema è di primo grado, le soluzioni in generale devono essere positive; sono da accettare anche, in taluni casi, soluzioni negative previa opportuna interpretazione.
Se il problema è di secondo grado, le soluzioni devono essere innanzitutto reali; ciò esclude che fra le operazioni necessarie, per ricavarle si possono estrarre radici quadrate di numeri negativi. Le condizioni di realtà escludono quindi che le operazioni sotto il segno di radice quadrate diano luogo a numeri negativi.
Notevole interesse possono presentare nei problemi letterali certe soluzioni per valori particolari di quelli dati; è bene metterle in evidenza e trattarle a parte.
Con le indicazioni date, si risolvono ora alcuni problemi.
Problema 1) - L'altezza di un triangolo isoscele è cm 48, il raggio del cerchio inscritto cm 18; calcolare il perimetro del triangolo.
Sia dato il triangolo ABC e O il centro del cerchio inscritto. I dati sono quindi:
Si ha:
e
Dai triangoli simili AOE ed ACD, si ricava la proporzione:
ossia
da cui
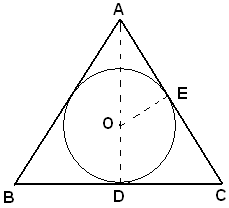
si ottiene
Infine,
il perimetro di ABC = cm (60 + 60 +72) =192,
l'area di ABC = cm2 (36 x 18) = cm2 1728.
Problema 2) - In una circonferenza di raggio r si conduca un diametro ed una semiretta ad esso perpendicolare distante a dal centro. Determinare il raggio della circonferenza tangente al diametro, alla semicorda ed internamente alla circonferenza data.
Nella figura seguente è indicata la circonferenza di raggio r, di centro O e la corda perpendicolare in C al diametro. Per l'enunciato è:
Si assume come grandezza incognita il raggio O'H della circonferenza, perciò si pone:
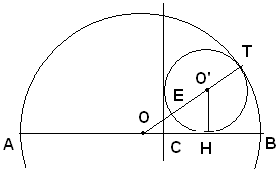
Trattazione del problema
Si congiunga O con O' e si prolunghi la congiungente; questa incontrerà le due circonferenze nel loro punto di tangenza T e la circonferenza di centro O' nel punto E.
Applicando il teorema della tangente e della secante, ha:
q (OH) = rett. (OT, OE)
e passando alle misure, poichè è
e
si ha
(a + x)2 = r(r - 2x).
Risoluzione dell'equazione
Sviluppando e ordinando, si ha:
a2 + 2ax + x2 = r 2 - 2rx,
x2 + 2(a + r)x + (a2 - r 2) = 0,
da cui
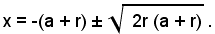
Discussione
Le radici dell'equazione sono reali e poichè a<r, l'equazione presenta una permanenza e una variazione e perciò dà una sola radice positiva, la minore in valore assoluto. Scartando il segno negativo davanti al radicale, si ha che l'unica soluzione del problema è:
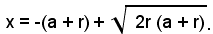
Casi particolari

cioè il raggio del cerchio in questione sarebbe uguale alla differenza fra il lato e l'altezza del triangolo equilatero inscritto nel cerchio dato.
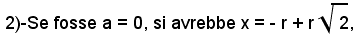
(a + x)2 = r(r - 2x).
Risoluzione dell'equazione
Sviluppando e ordinando, si ha:
x2 + 2(a + r)x + (a2 - r 2) = 0,
da cui
Discussione
Le radici dell'equazione sono reali e poichè a<r, l'equazione presenta una permanenza e una variazione e perciò dà una sola radice positiva, la minore in valore assoluto. Scartando il segno negativo davanti al radicale, si ha che l'unica soluzione del problema è:
Casi particolari
cioè il raggio del cerchio in questione sarebbe uguale alla differenza fra il lato e l'altezza del triangolo equilatero inscritto nel cerchio dato.
cioè il raggio del cerchio in questione sarebbe uguale alla differenza fra il lato del quadrato inscritto nel cerchio dato e lo stesso cerchio.