MIKY & GENNY
PARALLELOGRAMMI E FASCIO DI RETTE PARALLELE ---> INDICE
PARALLELOGRAMMI
Dicesi parallelogrammo un quadrangolo i cui lati opposti sono paralleli.
Due lati opposti del parallelogrammo si chiamano basi, mentre la loro distanza si chiama altezza.
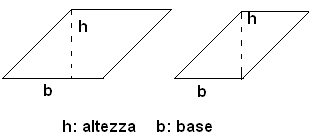
Due lati opposti del parallelogrammo si chiamano basi, mentre la loro distanza si chiama altezza.

Il parallelogrammo è una figura convessa. Infatti, si può considerare come formato dalla parte comune a due strisce ciascuna limitata dalle parallele a cui appartengono due lati opposti e le strisce sono figure convesse.
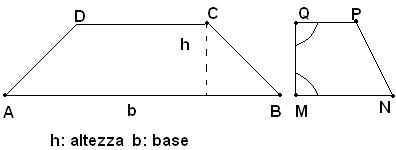
Dicesi trapezio un quadrilatero con soli due lati paralleli.
I lati paralleli si chiamano basi del trapezio, la loro distanza, altezza.
Un trapezio si dice isoscele se i due lati non paralleli sono uguali.
Un trapezio si dice rettangolo se uno dei due lati non paralleli è perpendicolare alle basi.
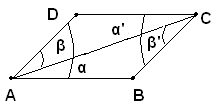
Teorema - Un parallelogrammo è diviso da una sua diagonale in due triangoli uguali.
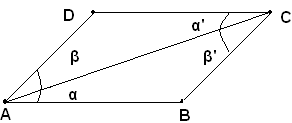
Ipotesi: sia AB una diagonale del parallelogrammo ABCD.
Tesi: si vuole dimostrare che i due triangoli ABC e ADC in cui il parallelogrammo è diviso dalla diagonale AC sono uguali.
Dimostrazione
Infatti, i due triangoli ABC e ADC hanno il lato AC in comune, gli angoli α e α' uguali , perchè alterni interni fra le parallele AB e CD e la trasversale AC, ed uguali gli angoli β e β', perchè
alterni interni fra le parallele AD e BC e la stessa trasversale AC;
pertanto, per il secondo criterio di uguaglianza dei triangoli, i due
triangoli ABC, ADC sono uguali.
Teorema - In un parallelogrammo si verifica quanto segue:
1)-i lati opposti sono uguali;
2)-gli angoli opposti sono uguali;
3)-le diagonali si dimezzano scambievolmente.
Ipotesi: sia dato il parallelogrammo ABCD.
Tesi: si vuole dimostrare che:
1)-sono uguali i lati opposti AB=DC e AD=BC,
2)-sono uguali gli angoli opposti δ=δ',
3)-le diagonali s'intersecano in un punto O che divide ciascuna di esse in parti uguali, cioè AO=OC, BO=OD.
Le tre parti del teorema si dimostrano separatamente.
Dimostrazione 1)
Per il teorema precedente, la diagonale AC divide il parallelogrammo ABCD in due triangoli ABC, ADC uguali, quindi sono uguali i lati opposti agli angoli uguali, cioè AD=BC, opposti rispettivamente agli angoli α' e α e AB=DC, opposti rispettivamente agli angoli β' e β, come volevasi dimostrare.
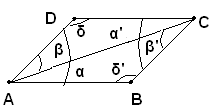
Dimostrazione 2)
Dall'uguaglianza dei due triangoli ABC e ADC segue l'uguaglianza degli angoli in B e in D, δ' e δ, opposti al lato comune AC e l'uguaglianza degli angoli in A e in C, in quanto somme di angoli rispettivamente uguali: α+α' e β+β'.
Dimostrazione 3)
Si indica con O il punto d'intersezione delle due diagonali, che certamente s'intersecano, perchè gli estremi dell'una stanno dalla parte opposta rispetto all'altra. I due triangoli AOB e COD hanno uguali i lati AB e DC, perchè sono lati opposti del parallelogrammo, gli angoli α e α' uguali, perchè alterni interni fra le parallele AB e DC e la trasversale AC e gli angoli β e β' uguali, perchè alterni interni fra le stesse parallele e la trasversale BD; sono quindi uguali. Segue che AO=OC, perchè opposti agli angoli uguali β e β' e BP=DO, perchè opposti agli angoli uguali α e α'
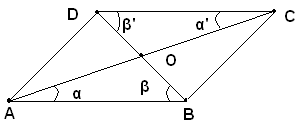
Teorema - Un quadrangolo è un parallelogrammo:
1)-se ha uguali le coppie dei lati opposti; oppure
2)-se ha uguali le coppie di angoli opposti; oppure
3)-se le diagonali si dimezzano scambievolmente.
Le tre parti del teorema si dimostrano separatamente.
Ipotesi 1) - nel quadrilatero ABCD sono uguali i lati opposti AB e DC ed uguali gli altri due lati opposti AD e BC.
Tesi: si vuole dimostrare che il quadrilatero è un parallelogrammo.
Dimostrazione 1)
Infatti, i due triangoli ABC, ADC sono uguali, perchè hanno i tre lati rispettivamente uguali, AB=CD e AD=BC, per ipotesi, ed AC in comune. Allora, sono uguali gli angoli opposti al vertice α e α', perchè opposti ai lati uguali BC, AD, e siccome sono alterni fra le rette AB e DC, queste sono parallele. Inoltre, sono anche uguali gli angoli β e β', perchè opposti ai lati uguali DC e AB; e siccome sono alterni interni fra la trasversale AC e le rette AD e BC, queste sono anche parallele. Il quadrilatero ABCD, avendo i lati opposti paralleli, è un parallelogrammo.
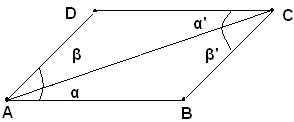
Ipotesi 2): nel quadrilatero ABCD siano uguali gli angoli opposti in A e in C, α e α', e gli angoli opposti in B e in D, β e β'.
Tesi: si vuole dimostrare che il quadrilatero è un parallelogrammo.
Dimostrazione 2)
Dimostrazione 2)
Poichè α=α' e β=β',
si ha che la somma degli angoli in A e in B è uguale alla
somma degli angoli in C e in D, cioè: α+β=α'+β',
e poichè la somma degli angoli di un quadrilatero è
uguale a quattro angoli retti, ciascuna delle due somme precedenti α+β e α'+β' è uguale a due angoli retti. Pertanto gli angoli in A e in B, α e β,
sono supplementari e siccome sono coniugati interni fra la trasversale
AB e le rette AD e BC, queste sono parallele. Analogamente si dimostra
che sono parallele le rette AB e DC. Il quadrangolo ABCD, avendo i lati opposti paralleli è un parallelogrammo.
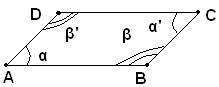
Ipotesi 3): nel quadrilatero ABCD le due diagonali AC e BD hanno lo stesso punto medio O.
Tesi: si vuole dimostrare che il quadrilatero è un parallelogrammo.
Dimostrazione 3)
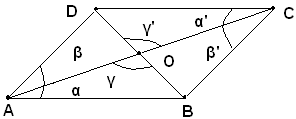
Infatti, i due triangoli AOB e COD sono uguali, perchè hanno AO=OC, BO=OD per ipotesi, e uguali gli angoli γ e γ', perchè opposti al vertice; sono quindi uguali gli angoli α e α',
opposti ai lati uguali BO e OD, e siccome sono alterni interni fra la
trasversale AC e le rette AB e DC, queste sono parallele. Analogamente si dimostra che sono paralleli i lati AB, DC. Il quadrangolo ABCD, avendo le coppie di lati opposti paralleli è un parallelogrammo.Dimostrazione 3)
Teorema - Un quadrangolo avente due lati opposti uguali e paralleli è un parallelogrammo.
Ipotesi: nel quadrilatero ABCD sono uguali e paralleli i lati opposti AB e DC.
Tesi: si vuole dimostrare che il quadrilatero è un parallelogrammo.
Dimostrazione
Condotta la diagonale AC, si ottengono i due triangoli ABC e CDA, che sono uguali per il primo criterio di uguaglianza, perchè hanno il lato AC in comune, uguali per ipotesi i lati AB e DC ed uguali gli angoli α e α', perchè alterni interni fra le parallele AB e DC e la trasversale AC; quindi hanno uguali gli angoli β' e β, opposti ai lati uguali AB, DC. Siccome questi angoli sono alterni interni fra la trasversale AC e le rette AD e BC, queste rette sono dunque parallele ed il quadrilatero ABCD, avendo le coppie di lati opposti paralleli è un parallelogrammo.
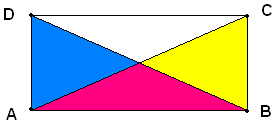
RETTANGOLO
Dicesi rettangolo un parallelogrammo che ha tutti gli angoli uguali, e quindi retti.Se
in un parallelogrammo un angolo è retto, anche gli altri tre
risultano retti: l'opposto, perchè uguale, e i consecutivi,
perchè supplementari.
Un quadrangolo equiangolo è un rettangolo, perchè è un parallelogrammo con tutti gli angoli retti.
Condotta la diagonale AC, si ottengono i due triangoli ABC e CDA, che sono uguali per il primo criterio di uguaglianza, perchè hanno il lato AC in comune, uguali per ipotesi i lati AB e DC ed uguali gli angoli α e α', perchè alterni interni fra le parallele AB e DC e la trasversale AC; quindi hanno uguali gli angoli β' e β, opposti ai lati uguali AB, DC. Siccome questi angoli sono alterni interni fra la trasversale AC e le rette AD e BC, queste rette sono dunque parallele ed il quadrilatero ABCD, avendo le coppie di lati opposti paralleli è un parallelogrammo.

RETTANGOLO
Dicesi rettangolo un parallelogrammo che ha tutti gli angoli uguali, e quindi retti.
Un quadrangolo equiangolo è un rettangolo, perchè è un parallelogrammo con tutti gli angoli retti.

Teorema - Il rettangolo ha le diagonali uguali.
Ipotesi: sia ABCD un rettangolo.
Tesi: si vuole dimostrare che le diagonali AC e BD sono uguali.
DimostrazioneInfatti, due triangoli ABD e BAC, rettangoli per ipotesi, rispettivamente in A e in B, hanno in comune ed uguali gli altri due cateti AD e BC, perchè lati opposto del rettangolo. I due triangoli sono dunque uguali ed hanno perciò uguali le ipotenuse BD e AC.
Teorema - Un parallelogrammo con le diagonali uguali è un rettangolo.
Ipotesi: il parallelogrammo ABCD ha le diagonali uguali BD e AC.
Tesi: si vuole dimostrare che ABCD è un rettangolo.
Dimostrazione
Infatti, i due triangoli BAD e ABC hanno il lato AB in comune, uguali i lati AD, BC, perchè lati opposto del parallelogrammo, ed uguali per ipotesi, i lati BD e AC; quindi sono uguali, per il terzo criterio di uguaglianza. Pertanto essi hanno uguali gli angoli in A e in B, opposti ai lati uguali BD e AC. Allora tutti gli angoli del parallelogrammo risultano unguali, cioè retti. ll parallelogrammo ABCD perciò è un rettangolo.
ROMBO
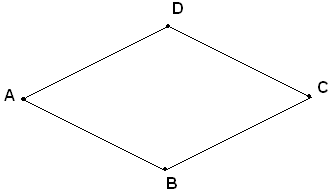
Dicesi rombo un parallelogrammo che ha tutti i lati uguali.
Un parallelogrammo che ha uguali i due lati consecutivi è un rombo, perchè ha uguali tutti e quattro i lati. Un quadrangolo con tutti i lati uguali è un rombo, perchè è un parallelogrammo con tutti i lati uguali.
Teorema - In un rombo le diagonali sono perpendicolari e bisecano gli angoli.
Dimostrazione
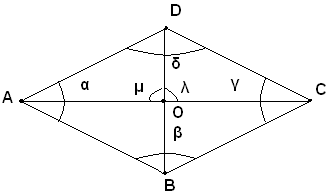
Sia O il punto d'incontro delle diagonali. I due triangoli AOD e, COD sono uguali per il terzo criterio di uguaglianza, in quanto hanno in comune OD, AO=OC, perchè le diagonali di un parallelogrammo si bisecano e AD=DC, per ipotesi. Sono dunque uguali gli angoli μ e λ, opposti a i lati uguali AD e DC, perciò le diagonali AC e BD formando angoli adiacenti uguali, sono perpendicolari. Dall'uguaglianza degli stessi triangoli risulta inoltre l'angolo in D e lati DA e DO uguale all'angolo in D e lati DO e DC, e ciò prova che DO è la bisettrice dell'angolo di vertice D e lati DA e DC del rombo. Analogamente si dimostra che BD biseca l'angolo β, e che la diagonale AC biseca gli angoli α e γ.
Teorema - Un parallelogrammo è un rombo:
1)-se le diagonali sono perpendicolari, oppure
2)-se una diagonale è bisettrice di uno degli angoli.
Ognuna delle due parti del teorema si dimostra separatamente.
Dimostrazione 1)
Infatti, si indica con O il punto d'intersezione delle due diagonali e si considerano i triangoli AOD e DOC: essi hanno gli angoli μ e λ retti per ipotesi, il cateto DO in comune ed uguali i cateti AO e OC, perchè la diagonale AC è dimezzata da BD; i due triangoli sono dunque uguali ed hanno pertanto uguali le ipotenuse AD e DC, quindi risulta che il parallelogrammo ABCD, avendo uguali due lati consecutivi, è un rombo.

Ipotesi 2): nel parallelogrammo ABCD la diagonale BD è la bisettrice dell'angolo β, cioè divide quest'angolo nei due angoli uguali AB e CD.Tesi: si vuole dimostrare che il parallelogrammo è un rombo.
Dimostrazione 2)
Infatti, i due angoli di vertice in B e lati BD e BC e vertice in D e lati DB e DA, sono uguali, perchè alterni interni fra le parallele BC e AD, e la trasversale BD; siccome i due angoli di vertice in B e lati BD, BC e vertice B e lati BA e BD sono uguali per ipotesi, per la proprietà transitiva, si ha che l'angolo di vertica B e lati BA e BD è uguale all'angolo di vertice D e lati DB e DA, quindi il triangolo ABD è isoscele sulla base BD. Allora segue che AB=AD e quindi il parallelogrammo, avendo due lati consecutivi uguali, è un rombo.
QUADRATO
Dicesi quadrato un parallelogrammo che ha tutti i lati e tutti gli angoli uguali.
Il quadrato costruito su un segmento dicesi quadrato del segmento. Se un quadrandolo è equilatero ed equiangolo è quadrato. Il quadrato è rombo e rettangolo nello stesso tempo, perchè ha tutti i lati e tutti gli angoli uguali.
Da ciò si deduce il seguente
Teorema - In un quadrato le diagonali sono uguali, perpendicolari e bisettrici degli angoli. Viceversa, un parallelogrammo è un quadrato:
1)-se le sue diagonali sono uguali e perpendicolari, oppure
2)-se le diagonali sono uguali ed una dI esse è bisettrice di un angolo del parallelogrammo.
FASCIO DI RETTE PARALLELE
Dicesi fascio di rette parallele l'insieme di tre o più rette parallele.
Dicesi trasversale di un fascio, una retta che interseca tutte le rette del fascio.
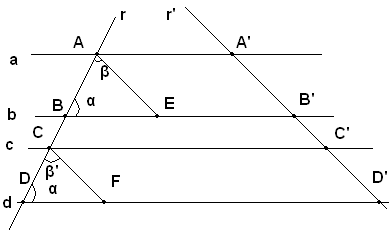
Se si taglia un fascio di rette parallele con due trasversali, si dicono corrispondenti i segmenti che su queste hanno gli estremi sulle stesse parallele. Nella figura seguente, se AA', BB', CC'. sono le rette parallele di un fascio tagliate dalle trasversali r e r', sono corrispondenti i segmenti AB e A'B', BC e B'C', ecc.
Teorema - Se un fascio di rette è tagliato da due trasversali, a segmenti uguali sull'una corrispondono segmenti uguali sull'altra.
Infatti, per i punti A e C si conducono le parallele alla trasversale r', e siano E ed F i rispettivi punto d'incontro con le parallele b e d. I due triangoli ABE e CDF risultano uguali perchè hanno i lati AB e CD uguali per ipotesi, uguali gli angoli α e α', perchè corrispondenti fra le parallele BE e DF, tagliate dalla trasversale r, ed uguali gli angoli β e β', perchè corrispondenti rispetto alle parallele AE e CF tagliate dalla stessa trasversale r. Segue che AE=CF. Ora AE=A'D', perchè lati opposti di un parallelogrammo e CF=C'D' per lo stesso motivo. Risultano dunque uguali fra loro A'B' e C'D'.
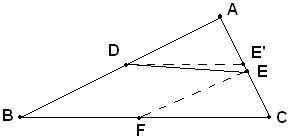
Teorema - La congiungente i punti medi di due lati di un triangolo è parallela al terzo lato ed è la metà di esso.
Dimostrazione
Supponendo che DE non è parallelo a BC, per il punto D si traccia DE' parallelo a BC. Poichè per ipotesi è AD=DB, risulta AE'=E'C, cioè E' è punto medio di AC. E ciò non è possibile, perchè altrimenti esistono due punti medi del segmento AC, E ed E'. Dev'essere quindi necessariamente DE parallelo a BD. Si dimostra ore che DE è la metà di BC. Si congiunge E con il punto medio F di BC; risulta EF parallelo ad AB, per la prima parte di questo teorema; dunque il quadrilatero BDEF è un parallelogrammo perchè ha i lati opposti paralleli. E perciò DE=BF; ma BF è uguale alla metà di BC per costruzione, dunque anche DE è uguale alla metà di BC.
Dimostrazione
Infatti, i due triangoli BAD e ABC hanno il lato AB in comune, uguali i lati AD, BC, perchè lati opposto del parallelogrammo, ed uguali per ipotesi, i lati BD e AC; quindi sono uguali, per il terzo criterio di uguaglianza. Pertanto essi hanno uguali gli angoli in A e in B, opposti ai lati uguali BD e AC. Allora tutti gli angoli del parallelogrammo risultano unguali, cioè retti. ll parallelogrammo ABCD perciò è un rettangolo.
ROMBO
Dicesi rombo un parallelogrammo che ha tutti i lati uguali.
Un parallelogrammo che ha uguali i due lati consecutivi è un rombo, perchè ha uguali tutti e quattro i lati. Un quadrangolo con tutti i lati uguali è un rombo, perchè è un parallelogrammo con tutti i lati uguali.

Teorema - In un rombo le diagonali sono perpendicolari e bisecano gli angoli.
Ipotesi: siano AC e BD ha le diagonali di un rombo ABCD.
Tesi:
si vuole dimostrare che AB e CD sono perpendicolari e che bisecano gli
angoli α, β, γ e δ del rombo.Dimostrazione
Sia O il punto d'incontro delle diagonali. I due triangoli AOD e, COD sono uguali per il terzo criterio di uguaglianza, in quanto hanno in comune OD, AO=OC, perchè le diagonali di un parallelogrammo si bisecano e AD=DC, per ipotesi. Sono dunque uguali gli angoli μ e λ, opposti a i lati uguali AD e DC, perciò le diagonali AC e BD formando angoli adiacenti uguali, sono perpendicolari. Dall'uguaglianza degli stessi triangoli risulta inoltre l'angolo in D e lati DA e DO uguale all'angolo in D e lati DO e DC, e ciò prova che DO è la bisettrice dell'angolo di vertice D e lati DA e DC del rombo. Analogamente si dimostra che BD biseca l'angolo β, e che la diagonale AC biseca gli angoli α e γ.

Teorema - Un parallelogrammo è un rombo:
1)-se le diagonali sono perpendicolari, oppure
2)-se una diagonale è bisettrice di uno degli angoli.
Ognuna delle due parti del teorema si dimostra separatamente.
Ipotesi 1): nel parallelogrammo ABCD le diagonali AB e CD sono perpendicolari.
Tesi: si vuole dimostrare che il parallelogrammo è un rombo.Dimostrazione 1)
Infatti, si indica con O il punto d'intersezione delle due diagonali e si considerano i triangoli AOD e DOC: essi hanno gli angoli μ e λ retti per ipotesi, il cateto DO in comune ed uguali i cateti AO e OC, perchè la diagonale AC è dimezzata da BD; i due triangoli sono dunque uguali ed hanno pertanto uguali le ipotenuse AD e DC, quindi risulta che il parallelogrammo ABCD, avendo uguali due lati consecutivi, è un rombo.

Ipotesi 2): nel parallelogrammo ABCD la diagonale BD è la bisettrice dell'angolo β, cioè divide quest'angolo nei due angoli uguali AB e CD.
Dimostrazione 2)
Infatti, i due angoli di vertice in B e lati BD e BC e vertice in D e lati DB e DA, sono uguali, perchè alterni interni fra le parallele BC e AD, e la trasversale BD; siccome i due angoli di vertice in B e lati BD, BC e vertice B e lati BA e BD sono uguali per ipotesi, per la proprietà transitiva, si ha che l'angolo di vertica B e lati BA e BD è uguale all'angolo di vertice D e lati DB e DA, quindi il triangolo ABD è isoscele sulla base BD. Allora segue che AB=AD e quindi il parallelogrammo, avendo due lati consecutivi uguali, è un rombo.
QUADRATO
Dicesi quadrato un parallelogrammo che ha tutti i lati e tutti gli angoli uguali.

Il quadrato costruito su un segmento dicesi quadrato del segmento. Se un quadrandolo è equilatero ed equiangolo è quadrato. Il quadrato è rombo e rettangolo nello stesso tempo, perchè ha tutti i lati e tutti gli angoli uguali.
Da ciò si deduce il seguente
Teorema - In un quadrato le diagonali sono uguali, perpendicolari e bisettrici degli angoli. Viceversa, un parallelogrammo è un quadrato:
1)-se le sue diagonali sono uguali e perpendicolari, oppure
2)-se le diagonali sono uguali ed una dI esse è bisettrice di un angolo del parallelogrammo.
Dicesi fascio di rette parallele l'insieme di tre o più rette parallele.
Dicesi trasversale di un fascio, una retta che interseca tutte le rette del fascio.
Se si taglia un fascio di rette parallele con due trasversali, si dicono corrispondenti i segmenti che su queste hanno gli estremi sulle stesse parallele. Nella figura seguente, se AA', BB', CC'. sono le rette parallele di un fascio tagliate dalle trasversali r e r', sono corrispondenti i segmenti AB e A'B', BC e B'C', ecc.
Teorema - Se un fascio di rette è tagliato da due trasversali, a segmenti uguali sull'una corrispondono segmenti uguali sull'altra.
Ipotesi:
si suppone che le rette a, d, c, d di un fascio di rette parallele
determinano su una trasversale r due segmenti uguali AB e CD.
Tesi: si vuole dimostrare che i segmenti rispettivamente corrispondenti A'B' e C'D' determinati dalle stesse parallele su un'altra trasversale r' sono pure uguali fra loiro.
DimostrazioneInfatti, per i punti A e C si conducono le parallele alla trasversale r', e siano E ed F i rispettivi punto d'incontro con le parallele b e d. I due triangoli ABE e CDF risultano uguali perchè hanno i lati AB e CD uguali per ipotesi, uguali gli angoli α e α', perchè corrispondenti fra le parallele BE e DF, tagliate dalla trasversale r, ed uguali gli angoli β e β', perchè corrispondenti rispetto alle parallele AE e CF tagliate dalla stessa trasversale r. Segue che AE=CF. Ora AE=A'D', perchè lati opposti di un parallelogrammo e CF=C'D' per lo stesso motivo. Risultano dunque uguali fra loro A'B' e C'D'.

Teorema - La congiungente i punti medi di due lati di un triangolo è parallela al terzo lato ed è la metà di esso.
Ipotesi:
siano D e E i punti medi dei lati AB e AC del triangolo ABC.
Tesi: si vuole dimostrare che il segmento DE è parallelo al segmento BC e che DE è la metà di BC.Dimostrazione
Supponendo che DE non è parallelo a BC, per il punto D si traccia DE' parallelo a BC. Poichè per ipotesi è AD=DB, risulta AE'=E'C, cioè E' è punto medio di AC. E ciò non è possibile, perchè altrimenti esistono due punti medi del segmento AC, E ed E'. Dev'essere quindi necessariamente DE parallelo a BD. Si dimostra ore che DE è la metà di BC. Si congiunge E con il punto medio F di BC; risulta EF parallelo ad AB, per la prima parte di questo teorema; dunque il quadrilatero BDEF è un parallelogrammo perchè ha i lati opposti paralleli. E perciò DE=BF; ma BF è uguale alla metà di BC per costruzione, dunque anche DE è uguale alla metà di BC.
