MIKY & GENNY
POLIEDRI ---> INDICE
Definizione - Si chiama poliedro, convesso, la porzione di spazio limitata da quattro o più poligoni giacenti
in piani differenti e tali che ognuno dei lati sia comune a due di essi
e il piano di ciascuno lasci tutti gli altri da una stessa banda.
Per porzione di spazio limitata da più poligoni, si deve intendere l'insieme dei punti che, rispetto al piano di uno qualsiasi dei poligoni, stanno dalla stessa banda di tutti gli altri.
Per porzione di spazio limitata da più poligoni, si deve intendere l'insieme dei punti che, rispetto al piano di uno qualsiasi dei poligoni, stanno dalla stessa banda di tutti gli altri.
I poligoni si chiamano facce del poliedro.
I vertici dei poligoni si chiamano vertici del poliedro.
I lati dei poligoni si chiamano spigoli del poliedro.
Due facce si dicono consecutive o contigue se hanno uno spigolo in comune.
L'insieme delle facce si chiama contorno o superficie poliedrica chiusa.
Si chiamano diedri e angoloidi del poliedro, rispettivamente i diedri di due facce consecutive e gli angoloidi limitati da facce aventi in comune un vertice.
Un poliedro prende il nome dal numero delle sue facce; se il numero delle facce è:
-4, si chiama tetraedro;
-5, si chiama pentaedro;
-6, si chiama esaedro;
-7, si chiama ettaedro;
-8, si chiama ottaedro;
-10, si chiama decaedro;
-12, si chiama dodecaedro;
-20, si chiama icosaedro.
Dalla definizione e dal postulato di partizione dello spazio risulta che:
-il segmento che congiunge due punti interni di un poliedro, convesso, è interno al poliedro;
-il segmento che congiunge un punto interno con uno eaterno, incontra il contorno in un punto.
Prisma
Definizione - Si chiama prisma, un poliedro avente per facce due poligoni uguali con i lati ordinatamente paralleli e i parallelogrammi aventi per vertici quelli dei poligoni.
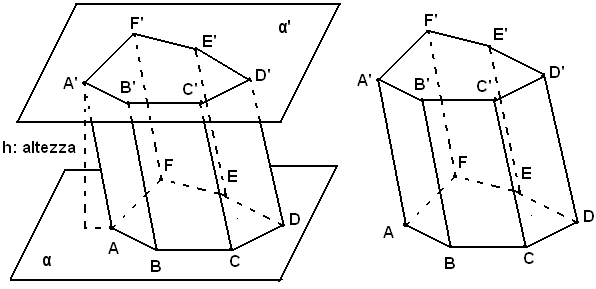
Dai vertici A, B, C, D, E di un poligono giacente in un piano α, si tracciano le parallele ad una retta data e non parallela ad α; esse incontrano un piano α' parallelo ad α nei punti A', B, C, D' E', che sono i vertici di un altro poligono uguale al primo e con i lati ad esso paralleli. Il poliedro, che ha per facce i due poligoni e i parallelogrammi ABB'A', BCC'B'..., ecc., è un prisma.
In un prisma le facce uguali, appartenenti a piani paralleli, si chiamano basi; le altre facce si chiamano facce laterali, o facce. Gli spigoli delle facce laterali non appartenenti alle basi si chiamano spigoli laterali, essi sono uguali. L'insieme delle facce laterali si chiama superficie laterale, l'insieme della superficie laterale e delle basi si chiama superficie totale del prisma.
La distanza fra le due basi si chiama altezza del prisma.
Quando il numero dei lati delle basi è:
-3, il prisma è triangolare,
-4, il prisma è quadrangolare,
-5, il prisma è pentagonale, ecc.
Un prisma si dice retto quando gli spigoli laterali sono perpendicolari alle basi; le sue facce sono rettangoli.
Un prisma non retto si dice obliquo.
Un prisma si dice regolare se è retto e le basi sono poligoni regolari.
Parallelepipedo
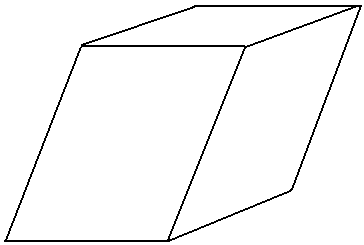
Definizione - Si chiama parallelepipedo un prisma avente per basi due parallelogrammi.
Siccome le facce di un prisma sono parallelogrammi, si ha che il parallelepipedo è un poliedro la cui superficie è formata da sei parallelogrammi. Il poliedro ABCDEFGH nella figura sottostante è un parallelepipedo.
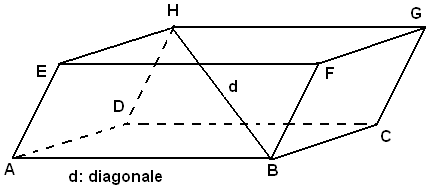
Due facce di un parallelepipedo si dicono opposte se non hanno alcuno spigolo in comune; due diedri o due triedri, le cui facce sono a due a due opposte,
Si chiamano diagonali del parallelepipedo i segmenti che congiungono due vertici opposti. Il parallelepipedo ha quattro diagonali.
Teorema - Le facce opposte del parallelepipedo sono uguali e parallele.
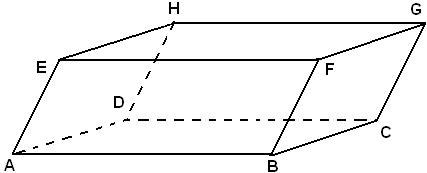
Sia ABCDEFGH un parallelepipedo, ABFE e DCGH due facce opposte. Poichè lo spigolo CG è parallelo a BF e CD è parallelo ad AB, il piano della faccia DCGH è parallelo a quello della faccia ABFE. Inoltre le facce considerate sono due parallelogrammi aventi uguali i lati AB e DC, BF e CG, e l'angolo fra questi compreso, perchè i lati in questione sono rispettivamente paralleli e concordi. Tali facce sono dunque uguali, come volevasi dimostrare.
Corollario - Un parallelepipedo si può considerare come prisma in tre modi diversi, assumendo come basi due facce opposte qualsiasi.
Parallelepipedo rettangolo
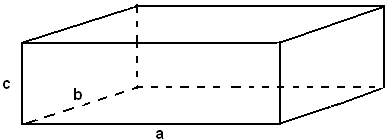
Definizione - Un parallelepipedo si dice rettangolo se è retto ed ha per basi due rettangoli.
Le sei facce del parallelepipedo rettangolo sono rettangoli. Ogni spigolo è perpendicolare a due facce opposte; i tre spigoli uscenti da uno stesso vertice sono a due a due perpendicolari. Le loro misure a, b, c, si chiamano dimensioni del parallelepipedo rettangolo.
Le sei facce del parallelepipedo rettangolo sono rettangoli. Ogni spigolo è perpendicolare a due facce opposte; i tre spigoli uscenti da uno stesso vertice sono a due a due perpendicolari. Le loro misure a, b, c, si chiamano dimensioni del parallelepipedo rettangolo.
Teorema - In un parallelepipedo rettangolo le diagonali sono uguali.
Sia ABCDEFGH un parallelepipedo rettangolo.
Si deve dimostrare che le quattro diagonali sono uguali.
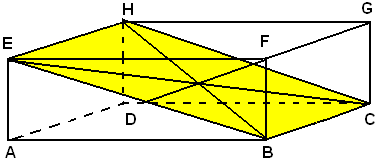
Infatti, si considerano prima due diagonali, BH e CE. Unito C con H e B con E, si ottiene il parallelogrammo BCHE, che è un rettangolo, perchè lo spigolo BC, essendo perpendicolare al piano della faccia DCGH, è perpendicolare alla retta CH che giace in questo piano e passa per il suo piede C; quindi l'angolo
Piramide
Definizione - Si chiama piramide, il poliedro che ha per facce un poligono qualsiasi e i triangoli che si ottengono congiungendo i vertici del poligono con un punto qualunque fuori dal suo piano.
La piramide si può considerare come porzione di un angoloide, che si trova dalla parte del vertice rispetto ad un piano, il quale taglia tutti gli spigoli.
In una piramide le facce triangolari si dicono facce laterali o facce; l'altra faccia può essere un poligono qualsiasi e si chiama base.
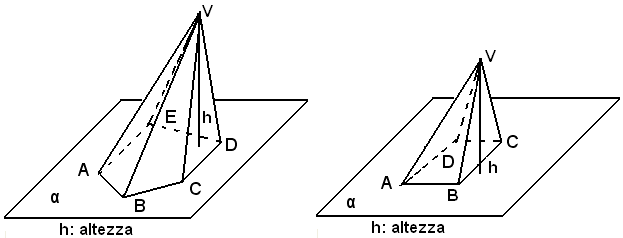
Il punto comune delle facce laterali si chiama vertice. I lati dei tre triangoli laterali non sulla base si dicono spigoli laterali o spigoli. L'altezza di una piramide è la distanza del vertice dal piano della base. Linsieme delle facce si chiama superficie laterale, la somma della superficie laterale e della base, superficie totale.
La piramide si dice:
-triangolare se il numero dei lati della base è uguale a 3,
-quadrangolare se il numero dei lati della base è uguale 4,
-pentagonale se il numero dei lati della base è uguale a 5, ecc.
Una piramide triangolare è un tetraedro. Un tetraedro si può considerare come una piramide, assumendo per base una faccia qualsiasi. In un tetraedro si dicono opposti due spigoli non appartenenti alla stessa faccia.
Una piramide di vertice V e di base ABCDE si indica con V (ABCDE).
Teorema - Se una piramide è tagliata da un piano parallelo alla base, si ha:
1)-la sezione è un poligono simile al poligono di base,
2)-i perimetri di questi poligoni stanno fra loro come le rispettive distanze dal vertice,
3)-le loro superfici stanno fra loro come i quadrati di queste distanze.
1)-Sia V (ABCDE) la piramide e A'B'C'D'E' una sua sezione parallela alla base ABCDE. Gli angoli del poligono ABCDE sono rispettivamente uguali a quelli del poligono A'B'C'D'E', perchè hanno i lati paralleli concordi.
Inoltre, dalla considerazione dei triangoli simili AVB e A'VB', si ha:
AB : A'B' = VB : VB'
e da quella degli altri due triangoli simili BVC, e B'VC', si ha anche
Una piramide triangolare è un tetraedro. Un tetraedro si può considerare come una piramide, assumendo per base una faccia qualsiasi. In un tetraedro si dicono opposti due spigoli non appartenenti alla stessa faccia.
Una piramide di vertice V e di base ABCDE si indica con V (ABCDE).
Teorema - Se una piramide è tagliata da un piano parallelo alla base, si ha:
1)-la sezione è un poligono simile al poligono di base,
2)-i perimetri di questi poligoni stanno fra loro come le rispettive distanze dal vertice,
3)-le loro superfici stanno fra loro come i quadrati di queste distanze.
1)-Sia V (ABCDE) la piramide e A'B'C'D'E' una sua sezione parallela alla base ABCDE. Gli angoli del poligono ABCDE sono rispettivamente uguali a quelli del poligono A'B'C'D'E', perchè hanno i lati paralleli concordi.
Inoltre, dalla considerazione dei triangoli simili AVB e A'VB', si ha:
AB : A'B' = VB : VB'
e da quella degli altri due triangoli simili BVC, e B'VC', si ha anche
BC : B'C' = VB : VB'.
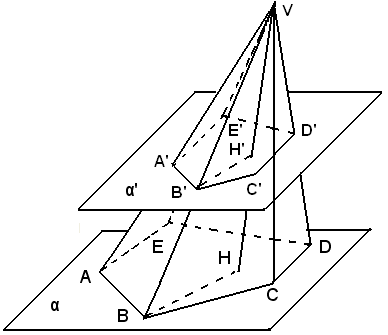
Confrontando le due proporzioni suddette, si ha:
AB : A'B' = BC : B'C'.
E così di seguito, risulta che i due poligoni ABCDE e A'B'C'D'E' hanno gli angoli rispettivamente uguali e i lati omologhi proporzionali, pertanto sono simili.
2)-Se P e P' sono i perimetri dei due poligoni, risulta:
P : P' = AB : A'B'.
Siccome
AB : A'B' = VB : VB'
e dalla considerazione dei triangoli simili VHB e VH'B' si ricava
VB : VB' = VH : VH'
e quindi
3)-Infine le superfici dei due poligoni stanno fra loro come i quadrati dei lati omologhi AB e A'B', ossia come i quadrati di VH e VH'.
Teorema - Due piramidi aventi uguali altezze e basi equivalenti, sono tagliate da piani paralleli alle basi ed equidistanti dai vertici, e quindi dalle basi, secondo poligoni equivalenti.
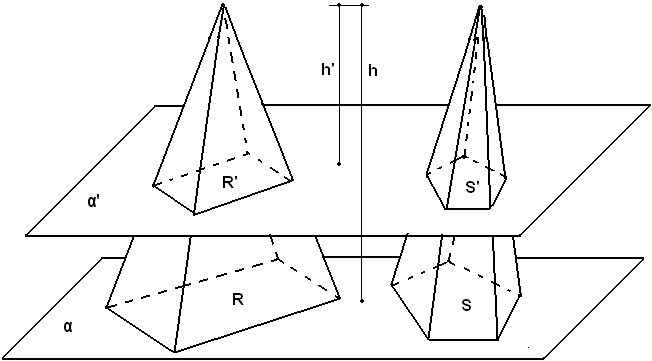
Infatti, se R ed S sono le loro basi ed R', S' le corrispondenti sezioni, per il teorema precedente, si ha:
R : S = R' : S'
e poichè R è equivalente ad S, risulta R' equivalente ad S'.
Piramide retta
Definizione - Una piramide si dice retta quando nel poligono di base si può inscrivere una circonferenza e il piede della perpendicolare abbassata dal vertice alla base coincide con il centro della circonferenza.
Una piramide non retta si dice obliqua.
Teorema - In una piramide retta le congiungenti il vertice con i punti di contatto dei lati della base con il cerchio inscritto sono le altezze dei triangoli delle facce; e sono tutte uguali fra loro.
1)-Sia data la piramide retta V (ABCD) e sia O il piede dell'altezza, coincidente con il centro del cerchio inscritto al poligono di base, e VE la congiungente il vertice con il punto E di contatto del cerchio con il lato AB.
Si dimostra dapprima che VE è la perpendicolare ad AB.
R : S = R' : S'
e poichè R è equivalente ad S, risulta R' equivalente ad S'.
Piramide retta
Definizione - Una piramide si dice retta quando nel poligono di base si può inscrivere una circonferenza e il piede della perpendicolare abbassata dal vertice alla base coincide con il centro della circonferenza.
Una piramide non retta si dice obliqua.
Teorema - In una piramide retta le congiungenti il vertice con i punti di contatto dei lati della base con il cerchio inscritto sono le altezze dei triangoli delle facce; e sono tutte uguali fra loro.
1)-Sia data la piramide retta V (ABCD) e sia O il piede dell'altezza, coincidente con il centro del cerchio inscritto al poligono di base, e VE la congiungente il vertice con il punto E di contatto del cerchio con il lato AB.
Si dimostra dapprima che VE è la perpendicolare ad AB.
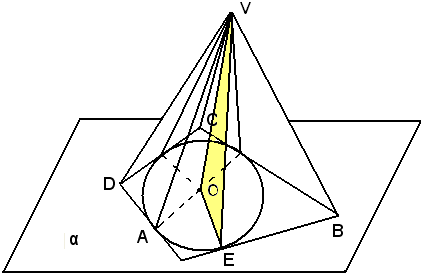
Infatti, le tre rette VO, OE ed AB si trovano nelle condizioni per l'applicazione del teorema delle tre perpendicolari, in quanto VO è perpendicolare al piano α della base e dal suo piede è condotta la perpendicolare OE alla retta AB di α. Ciò deriva dal fatto che OE è perpendicolare ad AB, perchè il raggio OE è perpendicolare nel suo punto di contatto alla tangente AB.
Quest'ultima retta è perpendicolare al piano delle prime due, cioè al piano OVE, quindi è perpendicolare a VE. E' dimostrato che VE è l'altezza della faccia AVB.
Per dimostrare che le altezze delle facce laterali sono tutte uguali fra loro, si osserva che esse hanno per proiezione raggi del cerchio inscritto. Siccome tali raggi sono uguali, altrettanto lo sono le altezze delle facce.
L'altezza di ciascuna faccia della piramide retta si chiama apotema.
Piramide regolare
Definizione - Una piramide si dice regolare se è retta ed ha per base un poligono regolare.
Teorema - In una piramide regolare gli spigoli laterali sono uguali fra loro e le facce sono triangoli isosceli uguali.
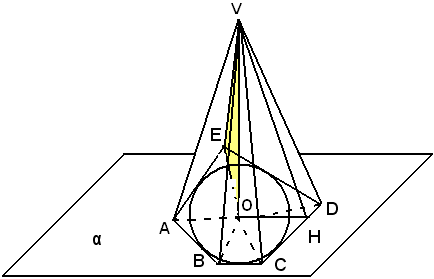
1)-Sia V (ABCDE) una piramide regolare. Gli spigoli laterali sono uguali perchè hanno per proiezioni OA, OB, OC, OD, OE che sono uguali fra loro perchè raggi del poligono regolare ABCDE.
Le facce laterali, avendo come lati gli spigoli laterali della piramide che si è visto essere uguali, sono triangoli isosceli; e poichè questi hanno le basi AB, BC, CD, DE, EA uguali, come lati di un poligono regolare, segue che le facce laterali della piramide sono triangoli isosceli tutti uguali fra loro.
Apotema di una piramide regolare è una qualsiasi delle altezze dei triangoli isosceli che costituiscono le facce.
L'apotema di una piramide regolare, essendo l'altezza dei triangoli isosceli delle facce, si ottiene congiungendo il vertice con il punto medio di uno dei lati della base.
Ad esempio, VH è l'apotema della piramide V (ABCDE), essendo H il punto medio di CD.
Tronco di piramide
Definizione - Si chiama tronco di piramide la parte di piramide che non contiene il vertice, ottenuta tagliando la piramide con un piano parallelo alla base.
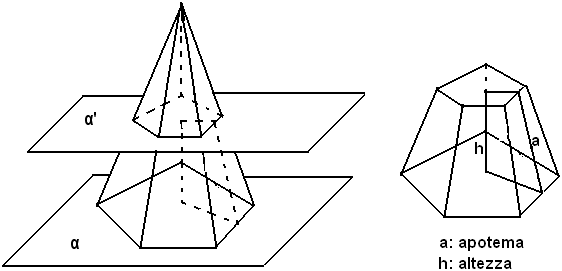
La base della piramide data e la sezione ottenuta con il piano parallelo si dicono basi, la loro distanza altezza del tronco. Si dicono facce le porzioni di facce della piramide comprese fra i piani paralleli: esse sono trapezi. Un tronco di piramide si dice retto o regolare a seconda che retta o regolare è la piramide da cui si ottiene. In un tronco di piramide retto o regolare, le facce sono trapezi di uguale altezza, che si chiama apotema del tronco.
Poliedri regolari
Definizione - Un poliedro si dice regolare, se le sue facce sono poligoni regolari uguali e gli angoloidi sono uguali fra loro.
Teorema - Non possono esistere più di cinque poliedri regolari.
Infatti, poichè le facce di un poliedro regolare devono essere poligoni regolari uguali fra loro, sono tutti triangoli equilateri o tutti quadrati, ecc. In ogni caso il numero della facce che possono concorrere in un vertice è limitato dal fatto che, dovendo formare un angoloide, la somma degli angoli dev'essere inferiore a quattro retti, ossia a 360°.
Si suppone dapprima che le facce sono triangoli equilateri.
In tal caso, in un vertice del poliedro potranno concorrere tre, quattro, o cinque facce, non di più, perchè nei primi tre casi la somma degli angoli in ciascun vertice è 3·60°; 4·60°; 5·60°, cioè meno di 360°, mentre, se nel vertice concorressero sei facce, la somma degli angoli sarebbe 6·60°, ovvero 360°, ed uguaglierebbe perciò quattro retti; e se concorressero più di sei, la somma supererebbe quattro retti.
Si suppone che le facce sono quadrati.
In tal caso, in un vertice possono concorrere tre facce e non di più, poichè se ne concorrono tre, la somma degli angoli nel vertice è 3·90° uguale a 270° che risulta minore di 360°, mentre se ne concorressero quattro, la somma delle facce sarebbe di 4·90° uguale a 360°, e se ne concorressero più di quattro, la somma sarebbe maggiore di 360°.
Si suppone che le facce sono pentagoni regolari.
In tal caso, in un vertice del poliedro possono concorrere tre facce e non di più, perchè se ne concorressero tre, la somma degli angoli in un vertice è 3·108° uguale a 324°, essendo l'angolo di un pentagono regolare di 108°; mentre se ne concorressero quattro, la somma delle facce sarebbe 4·108° uguale a 432°, che è maggiore di 360°, e se ne concorressero più di quattro, a maggior ragione la somma sarebbe maggiore di 360°.
Non possono esistere poliedri regolari le cui facce siano esagoni regolari o poligoni regolari con un numero di lati maggiore di sei, poichè la somma delle facce di ogni angoloide del poliedro supererebbe 360°.
Per questo basta osservare che, essendo l'angolo di un esagone regolare di 120°, nel caso più semplice che gli angoloidi siano diedri, la somma delle facce di ogni angoloide sarebbe 3·120° uguale a 360°, e in tutti gli altri casi sarebbe pertanto maggiore di 360°.
Quindi, I cinque poliedri regolari esistenti, e che si possono costruire, sono:
1)-il tetraedro con facce triangolari,
2)-l'esaedro o cubo con facce triangolari,
In tal caso, in un vertice del poliedro possono concorrere tre facce e non di più, perchè se ne concorressero tre, la somma degli angoli in un vertice è 3·108° uguale a 324°, essendo l'angolo di un pentagono regolare di 108°; mentre se ne concorressero quattro, la somma delle facce sarebbe 4·108° uguale a 432°, che è maggiore di 360°, e se ne concorressero più di quattro, a maggior ragione la somma sarebbe maggiore di 360°.
Non possono esistere poliedri regolari le cui facce siano esagoni regolari o poligoni regolari con un numero di lati maggiore di sei, poichè la somma delle facce di ogni angoloide del poliedro supererebbe 360°.
Per questo basta osservare che, essendo l'angolo di un esagone regolare di 120°, nel caso più semplice che gli angoloidi siano diedri, la somma delle facce di ogni angoloide sarebbe 3·120° uguale a 360°, e in tutti gli altri casi sarebbe pertanto maggiore di 360°.
Quindi, I cinque poliedri regolari esistenti, e che si possono costruire, sono:
1)-il tetraedro con facce triangolari,
2)-l'esaedro o cubo con facce triangolari,
4)-l'icosaedro con facce quadrate,
5)-il dodecaedro regolare con facce pentagonali.
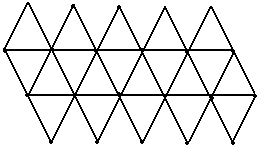
Si procede alla loro costruzione servendosi del loro sviluppo, ossia della figura che assume la loro superficie quando, supposta materializzata, venga tagliata opportunamente e distesa su un piano.
Tetraedro regolare
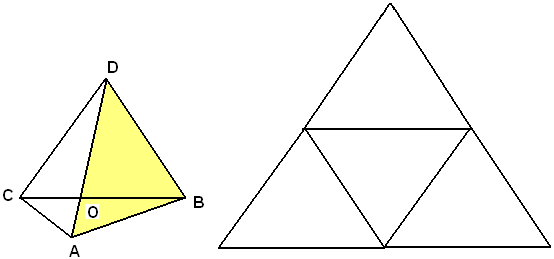
Il tetraedro regolare ha quattro facce triangolari e gli angoloidi sono triedri. Per la sua costruzione si opera come segue:
dal centro O di un triangolo equilatero ABC si innalza la perpendicolare al piano del triangolo, e su una delle semirette, nelle quali essa rimane divisa da O, si prende un punto D, la cui distanza dai tre vertici A, B, C, è uguale al lato del triangolo dato. Il poliedro che si ottiene congiungendo D con i vertici del triangolo è un tetraedro regolare, le facce sono tutti triangoli uguali al triangolo eqilatero ABC e gli angoloidi, essendo tutti triedri con facce uguali, sono uguali.
Il modello del tetraedro regolare si può costruire facilmente partendo dallo sviluppo della sua superficie come appare nella figura seguente.
Esaedro regolare o cubo
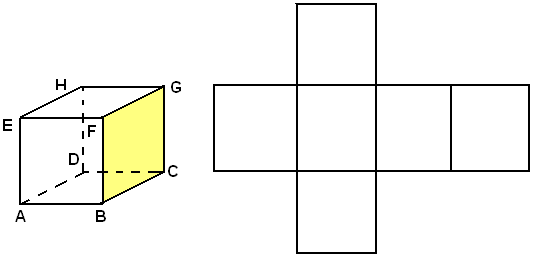
L'esaedro regolare o cubo ha sei facce quadrate e gli angoloidi sono triedri. Per la sua costruzione si opera come segue:
dai vertici di un quadrato ABCD si innalzano le perpendicolari al suo piano e su di esse, da una stessa banda, si prendono quattro segmenti AE, BF, CG, DH, uguali al lato del quadrato. Il poliedro ABCDEFGH è un esaedro regolare in quanto ha come facce sei quadrati uguali e gli angoloidi, che sono triedri, anche uguali. Alla costruzione di un modello di cubo si può pervenire partendo dallo sviluppo seguente.
Ottaedro
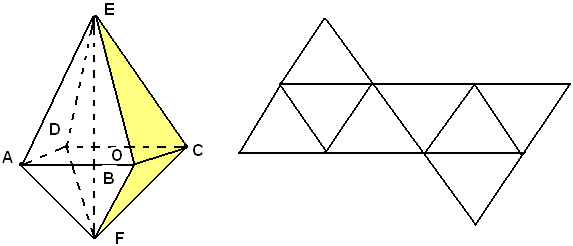
L'ottaedro ha otto facce triangolari e gli angoloidi sono tetraedri. Per la sua costruzione si opera come segue:
si innalza dal centro O di un quadrato ABCD una perpendicolare al suo piano e sulle due semirette in cui questa rimane divisa da O, si prendono due punti E ed F, le cui distanze dai punti A, B, C, D, sono uguali al lato del quadrato dato. Il poliedro che si ottiene congiungendo F, E, con i vertici del quadrato, ha otto facce che sono triangoli equilateri tutti uguali. Per provare che gli angoloidi, tetraedri, sono uguali, si fa ruotare l'ottaedro intorno alla retta EF in modo che A venga a coincidere con B; l'angoloide di vertice A verrà a coincidere con quello di vertice B, questo con l'angoloide di vertice C, ecc. Analogamente, considerando una rotazione intorno ad AC, si vede che gli angoloidi di vertici B, D, E, F sono uguali fra loro, e quindi ai precedenti. Pertanto, l'ottaedro costruito, avendo per facce triangoli equilateri uguali e gli angoloidi uguali, è regolare. Il modello di ottaedro regolare si può costruire partendo dallo sviluppo della sua superficie seguente.
Dodecaedro regolare
Il dodecaedro ha dodici facce pentagonali e gli angoloidi sono triedri. Ci si limita a riportare lo sviluppo della sua superficie come appare nella figura seguente.
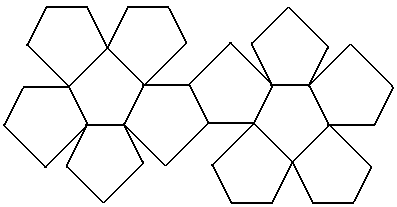
Da esso, opportunamente piegato, si può pervenire alla costruzione di un modello di questo poliedro.
Icosaedro regolare
L'icosaedro regolare ha venti facce e gli angoloidi sono pentaedri.
Ci si limita a riportare lo sviluppo della sua superficie, da esso si può facilmente risalire alla costruzione di un modello di icosaedro regolare.