MIKY & GENNY
RETTE E PIANI PARALLELI E PARALLELISMO ---> INDICE
Definizione - Una retta e un piano si dicono paralleli quando non hanno nessun punto in comune.
Teorema - Una retta esterna ad un piano e parallela ad una sua retta è parallela al piano.
Teorema - Una retta esterna ad un piano e parallela ad una sua retta è parallela al piano.
Sia assegnato il piano α, r la retta esterna ad α e parallela alla retta s di α.
Si dimostra che la retta r non incontra α.
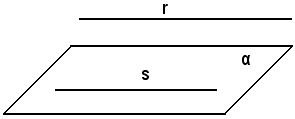
Infatti, l'intersezione della retta r con il piano α, se esistesse, dovrebbe essere o sulla retta s, o fuori di s; ma su s non può essere, perchè r ed s sono parallele per ipotesi, fuori di s nemmeno, perchè in tal caso r ed s sarebbero sghembe. Resta così dimostrato che r non incontra s.
Teorema - Se una retta è parallela ad un piano, ogni piano passante per la retta e che incontra il piano dato, taglia questo secondo una retta parallela alla data.
Sia α il piano dato, r una retta parallela ad α, β piano che passa per r e che taglia α secondo la retta s.
Si dimostra che la retta r è parallela ad s.
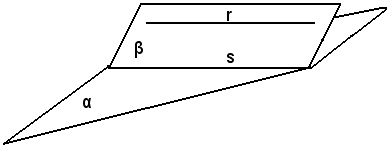
Infatti, è assurdo supporre che la retta r incontri la s, poichè in tal caso r incontrerebbe anche il piano α, contro l'ipotesi. Siccome r ed s stanno su uno stesso piano, si conclude che devono essere parallele.
Teorema - I punti di una retta parallela ad un piano sono equidiatanti dal piano.
Sia data la retta r parallela al piano α.
Si deve dimostrare che i punti della retta r sono equidistanti dal piano α.
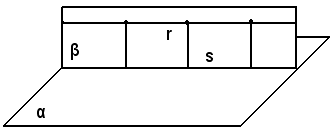
Si conduce per r il piano β perpendicolare ad α, e sia s l'intersezione di β con α; r ed s sono parallele per il teorema precedente. I punti di r sono equidistanti dalla retta s, e quindi anche dal piano α, poichè le perpendicolari abbassate dai punti di r alla s sono anche perpendicolari ad α.
Definizione- Data una retta parallela ad un piano, si chiama distanza della retta dal piano, la distanza di un punto qualsiasi della retta dal piano.
Piani paralleli
Definizione- Due piani si dicono paralleli se non hanno nessun punto in comune.
Teorema - Due piani perpendicolari ad una stessa retta in due punti distinti, sono paralleli.
Siano α e β due piani perpendicolari alla retta r nei punti distinti A e B.
Si deve dimostrare che α e β non hanno nessun punto in comune.
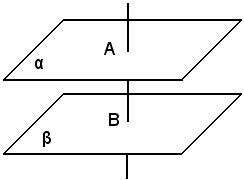
Infatti, qualora α e β avessero un punto in comune, per tale punto si potrebbero condurre due piani perpendicolari alla stessa retta, e ciò è assurdo per il teorema "Per un punto passa uno ed un solo piano, perpendicolare ad una retta data".
Teorema - Se due piani sono paralleli, tutte le rette dell'uno sono parallele all'altro; viceversa, se due piani sono paralleli, le rette parallele ad uno di essi, condotte per i punti dell'altro, stanno su questo.
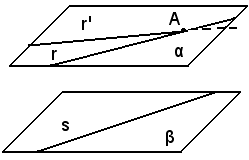
La prima parte è un'immediata conseguenza della definizione; si dimostra la seconda parte.
Siano α e β due piani paralleli e sia A un punto di α.
Si deve dimostrare che una retta r passante per A e parallela a β giace su α.
Infatti, si suppone per il momento che r non giaccia su α.
Si conduce per r e per un punto qualsiasi di β un terzo piano, questo taglia α lungo la retta r' passante per A e β lungo la retta s, e questa retta e la r' devono essere parallele perchè giacciono sullo stesso piano e non s'intersecano. Ma allora in uno stesso piano si avrebbero per uno stesso punto A due parallele r ed r' alla stessa retta s, il che è assurdo secondo il postulato di Euclide.
Sui piani paralleli sono importanti i seguenti teoremi, dei quali ci si limita solo all'enunciato.
Teorema - Per un punto esterno ad un piano si può condurre uno ed un solo piano parallelo a quello.
Teorema - Due piani paralleli ad un terzo sono paralleli fra loro.
Intersezioni di rette e piani con piani paralleli
Teorema - Se due piani sono paralleli, ogni retta che incontra l'uno incontra anche l'altro.
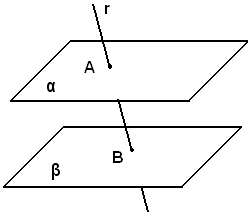
Siano α e β due piani paralleli ed r una retta che abbia con α un solo punto A in comune.
Si deve dimostrare che r incontra anche β.
Infatti, qualora r non incontrasse β, dovrebbe essere parallela a β, e in tal caso, avendo un punto A in comune con α, per un teorema precedente dovrebbe giacere su tale piano, mentre per ipotesi ha soltanto un solo punto in comune con esso. Dunque r incontra β, come volevasi dimostrare.
Teorema - Se due piani sono paralleli, ogni piano che incontra l'uno incontra l'altro e le intersezioni sono rette parallele.
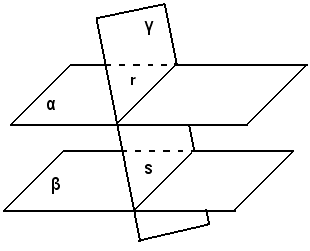
Siano α e β due piani paralleli e γ un piano che incontri α lungo una retta r.
Si deve dimostrare che γ taglia β lungo una retta s parallela ad r.
Intanto è certo che γ incontra β lungo una retta s, perchè diversamente dovrebbe essere parallela a β, e allora per un punto di r si potrebbero condurre due piani paralleli a β, contrariamente a quanti espresso da un teorema precedente. Inoltre, poichè r ed s non hanno alcun punto in comune e giacciono su uno stesso piano, sono parallele.
Teorema - Se due piani sono paralleli, ogni retta, od ogni piano, perpendicolare ad uno è perpendicolare anche all'altro.
Ci si limita solo all'enunciato.
Teorema di talete nello spazio
Un fascio di piani paralleli, cioè l'insieme di tre o più piani paralleli, determina su due trasversali segmenti direttamente proporzionali.
Siano α, β e γ tre piani parlleli, r ed r' due trasversali tagliate dai piani α, β e γ rispettivamente nei punti A, A'; B, B'; C, C'.
Si deve dimostrare che:
AB : BC = A'B' : B'C'
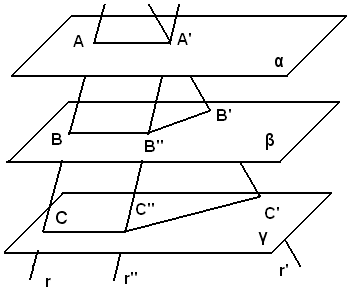
Infatti, dal punto A'' della trasversale r' si traccia la parallele r'' ad r e siano B'' e C'' le intersezioni con i piani β e γ. Le rette B'B'' e C'C'' appartengono al piano r'r'' e non s'incontrano. Dunque, sono parallele.
Applicando il teorema di Talete nel piano, si ha:
Siccome
A'B'' = AB e B''C'' = BC,
perchè lati opposti di un parallelogrammo, dalla proporzione precedente si ricava
AB : BC = A'B' : B'C',
come volevasi dimostrare.
Distanza fra piani paralleli
Siano α e β due piani paralleli, A ed A' due punti qualsiasi del piano α.
Si deve dimostrare che: le distanze AB e A'B' dal piano β sono uguali.
Si osserva prima che, essendo i piani α e β paralleli, AB che è perpendicolare a β, è anche perpendicolare ad α per un teorema precedente. Quindi AB rappresenta tanto la distanza del punto A di α dal piano β, quanto la distanza del punto B di β, dal piano α. Analogamente A'B' rappresenta tanto la distanza del punto A' dal piano β, quanto quella di B' dal piano α.
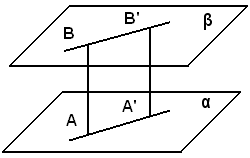
D'altra parte il quadrilatero ABB'A' è un rettangolo, perciò AB e A'B' sono uguali.
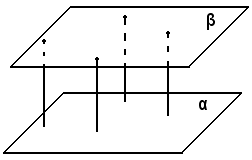
Definizione - Si chiama distanza di due piani paralleli la distanza di un punto qualunque di uno dei piani dall'altro.
Rette parallele
Teorema - Due rette perpendicolari ad un piano sono parallele.
Le rette a e b siano perpendicolari ad un piano α nei punti A e B.
Si deve dimostrare che: le rette a e b sono parallele.
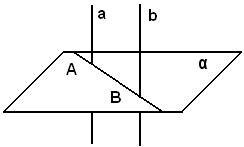
Infatti, il piano passante per α e per l'intersezione B della retta b con α è perpendicolare al piano α, per un teorema precedente, perciò contiene la perpendicolare b ad α uscente da B, per un corollario precedente. Quindi le rette a e b sono complanari e, poichè sono perpendicolari alla retta AB, sono parallele.
Altri due teoremi notevoli sulle rette parallele sono i seguenti, e ci si limita solo all'enunciato.
Teorema - Per un punto nello spazio si può condurre una ed una sola parallela ad una retta data.
Teorema - Due rette nello spazio parallele ad una terza sono parallele fra di loro.
Intersezioni di piani con rette parallele
Seguono altri teoremi notevoli, di cui ci si limita solo all'enunciato.
Teorema - Se due rette sono parallele, ogni piano che incontra l'una incontra anche l'altra.
Teorema - Se due rette sono parallele, ogni piano perpendicolare all'una è perpendicolare anche all'altra.
Angoli con lati paralleli
Se due angoli hanno i lati paralleli e concordi sono uguali.
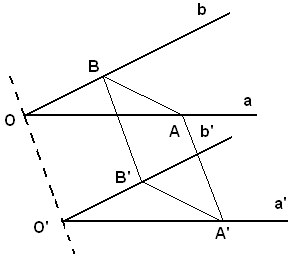
due angoli aventi i lati paralleli e concordi, precisamente a parallelo ad a' e b parallelo a b'.Si deve dimostrare che i due angoli sono uguali.
Il teorema è noto nel caso in cui i due angoli si trovino nello stesso piano.
Si suppone ora che essi si trovino su piani differenti.
Si staccano sui lati a e a', a partire dal vertice, i segmenti uguali OA e O'A' e sui lati b e b' i segmenti OB e O'B' anche uguali fra loro. Il quadrilatero OO'A'A è un parallelogrammo perchè ha i lati opposti OA E O'A' uguali e paralleli. Si ha quindi che il segmento OO' è uguale e parallelo a BB'; dunque AA' è uguale e parallelo a BB', quindi il quadrilatero ABA'B' è un parallelogrammo. Di conseguenza, AB = A'B'.
I due triangoli OAB e O'A'B' risultano uguali, perchè hanno i tre lati rispettivamente uguali e quindi
come angoli di due triangoli opposti a lati uguali, come volevasi dimostrare.Nota bene
Si può facilmente dimostrare che:
-se due angoli nello spazio hanno i lati paralleli e discordi, sono uguali; se hanno i lati paralleli uno concorde e uno discorde, sono supplementari.