MIKY & GENNY
RETTE PERPENDICOLARI ---> INDICE
DEFINIZIONE
E' noto che se due rette si incontrano determinano quattro angoli che sono a due a due uguali perchè opposti al vertice. Ora, se uno di tali angoli è retto, lo sono tutti e quattro, ed in tal caso le due rette si dicono perpendicolari, pertanto:
due rette si dicono perpendicolari quando si incontrano in un punto e formano quattro angoli retti uguali.
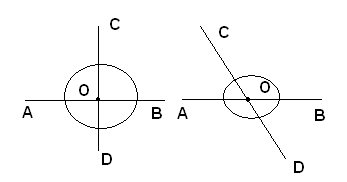
Due rette non perpendicolari si dicono oblique. Le due figure seguenti rappresentano rispettivamente due rette perpendicolari e due rette oblique.
Per poter asserire che due rette che si intersecano in un punto sono perpendicolari non è necessario accertarsi dell'uguaglianza di tutti i quattro angoli che esse formano, ma è sufficiente sapere che sono uguali solo due angoli adiacenti, poichè in tal caso è certi che sono uguali anche gli angoli rimanenti, opposti al verice a quelli, oppure basta sapere che uno dei quattro angoli è retto, in quanto sono retti gli altri tre, due dei quali sono adiacenti e l'altro opposto al vertice a quello.
Due semirette o segmenti si dicono perpendicolari se tali sono le rette a cui appartengono.
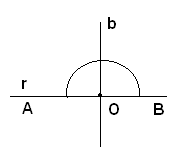
Per tracciare due rette perpendicolari si fa uso di una squadretta accoppiata ad una riga. Se, ad esempio si vuole tracciare la perpendicolare ad una retta a passante per un punto A, è sufficiente disporre la riga lungo la retta a, adattare uno dei lati all'angolo retto della squadretta in modo da farlo combaciare con lo spigolo della riga, e fare poi scorrere la squadretta finchè il secondo lato dell'angolo retto passi per A. Facendo scorrere la matita su tale lato della squadretta, si ottiene la perpendicolare b alla retta a, passante per il punto A e che interseca a neI punto B.
Teorema - Per un punto dato si può condurre una ed una sola retta perpendicolare ad una retta data.
Si distinguono due casi:
a)-il punto O appartiene alla retta r.
Sia r=AB la retta data e O un punto su di essa. E' noto che esiste la bisettrice di uno dei due angoli piatti di vertice O i cui lati OA e OB sono su una retta. Tale bisettrice b e la sua opposta formano la retta perpendicolare ad r. Siccome la bisettrice di un angolo è unica, tale è la perpendicolare alla retta AB in un punto O.
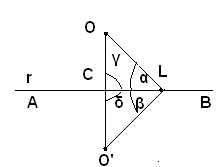
b)-Il punto O non appartiene alla retta r.Si
traccia una retta passante per O in modo che incontri la retta r in un
punto L. Se gli angoli in L sono retti, allora la retta AL è la
perpendicolare richiesta. Altrimenti, uno dei due angoli che essa forma
con la retta r è acuto. Se questo è l'angolo α, dal punto L si conduce una retta dalla parte opposta di O che formi con r un angolo uguale all'angolo α,
su di essa si stacca un segmento LO'=LO e si congiunge O con O'. A
tal punto si dimostra che la retta OO' è la perpendicolare da O
alla retta r. Infatti, detta C l'intersezione di di OO' con la retta r,
i triangoli COL e CO'L risultano uguali, perchè hanno il lato CL in
comune, OL=O'L per costruzione, ed uguale, anche per
costruzione, l'angolo fra essi compreso. Perciò risultano
uguali gli angoli
δ e γ,
opposti ai lati uguali O'L e OL. Le due rette r e OO', formando angoli
adiacenti uguali, sono perpendicolari. Nessun'altra retta passante per O
e distinta dalla OO' può essere perpendicolare alla r,
poichè se accadesse che, ad esempio, la OM
fosse anch'essa perpendicolare ad r, il triangolo OCM avrebbe due
angoli retti, il che è assurdo.
Corollario
Due rette perpendicolari alla stessa retta in due punti distinti non s'incontrano.
Infatti, se s'incontrassero in un punto, da questo si potrebbero condurre due perpendicolari distinte alla stessa retta.
Segmenti fra un punto ed una retta
In un piano si consideri una retta r ed un punto A non appartenente ad essa. Si conduca dal punto A la perpendicolare alla retta r e sia P il punto d'intersezione. Si congiunga A con un qualunque altro punto C di r, diverso da P.
Dicesi segmento di perpendicolare condotto da un punto A alla retta r, il segmento AP della perpendicolare alla retta compreso fra il punto e la retta stessa.
L'estremo P della perpendicolare alla retta si chiama piede della perpendicolare.
Ogni segmento che congiunge un punto dato A con un punto qualsiasi B di una retta, distinto da quello della perpendicolare, si dice linea obliqua, tale è il segmento AC. Il segmento AP prende il nome di distanza fra il punto A e la retta r.
Quindi, dicesi distanza del punto dalla retta, il segmento di perpendicolare abbassato dal punto alla retta.
In generale, dicesi distanza di un punto da una figura il più piccolo dei segmenti congiungente il punto con i punti della figura. Per distanza fra due punti s'intende il segmento che li unisce.
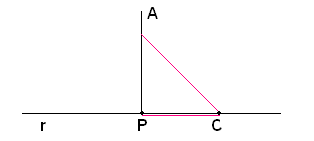
Proiezione di un punto sopra una retta
Se AP è il segmento di perpendicolare condotta dal punto A alla retta r e AC una qualsiasi linea obliqua, il segmento PC si dice proiezione del segmento AC sulla retta r. Quindi:
si chiama proiezione di un punto sopra una retta il piede della perpendicolare condotta dal punto alla retta.
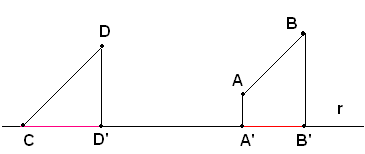
Proiezione di un segmento sopra una retta
Si chiama proiezione di un segmento sopra una retta il segmento che ha per estremi le proiezioni dei due estremi.
La proiezione del segmento CD, che ha l'estremo C sulla retta r, è il segmento CD', essendo D' la proiezione del punto D.La proiezione del segmento AB sulla retta r è il segmento A'B', essendo A' e B' le proiezioni dei punti A e B.
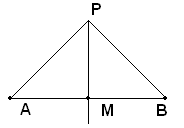
Asse di un segmento
Dicesi asse di un segmento la retta perpendicolare al segmento condotta ad un segmento nel suo punto medio.
Si può verificare che che preso un qualsiasi punto P sull'asse del segmento AB, sono uguali le distanze del punto considerato dagli estremi del segmento, pertanto risulta: AP=PB.
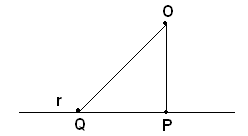
Teorema - Se da un punto si conducono la perpendicolare e delle oblique ad una retta:
1)-il segmento di perpendicolare è minore di ogni obliqua;
2)-se due oblique hanno proiezioni uguali sono uguali;
3)-se due oblique hanno proiezioni disuguali è maggiore quella che ha proiezione maggiore. E viceversa.1)-Sia OP il segmento di perpendicolare condotto da O ad una retta r e OQ un'obliqua, si vuole dimostrare che OP<OQ.
Infatti, nel triangolo rettangolo POQ, OP è un cateto e OQ l'ipotenusa, quindi OP<OQ.
E' noto che se due rette si incontrano determinano quattro angoli che sono a due a due uguali perchè opposti al vertice. Ora, se uno di tali angoli è retto, lo sono tutti e quattro, ed in tal caso le due rette si dicono perpendicolari, pertanto:
due rette si dicono perpendicolari quando si incontrano in un punto e formano quattro angoli retti uguali.
Due rette non perpendicolari si dicono oblique. Le due figure seguenti rappresentano rispettivamente due rette perpendicolari e due rette oblique.

Per poter asserire che due rette che si intersecano in un punto sono perpendicolari non è necessario accertarsi dell'uguaglianza di tutti i quattro angoli che esse formano, ma è sufficiente sapere che sono uguali solo due angoli adiacenti, poichè in tal caso è certi che sono uguali anche gli angoli rimanenti, opposti al verice a quelli, oppure basta sapere che uno dei quattro angoli è retto, in quanto sono retti gli altri tre, due dei quali sono adiacenti e l'altro opposto al vertice a quello.
Due semirette o segmenti si dicono perpendicolari se tali sono le rette a cui appartengono.
Per tracciare due rette perpendicolari si fa uso di una squadretta accoppiata ad una riga. Se, ad esempio si vuole tracciare la perpendicolare ad una retta a passante per un punto A, è sufficiente disporre la riga lungo la retta a, adattare uno dei lati all'angolo retto della squadretta in modo da farlo combaciare con lo spigolo della riga, e fare poi scorrere la squadretta finchè il secondo lato dell'angolo retto passi per A. Facendo scorrere la matita su tale lato della squadretta, si ottiene la perpendicolare b alla retta a, passante per il punto A e che interseca a neI punto B.
Teorema - Per un punto dato si può condurre una ed una sola retta perpendicolare ad una retta data.
Si distinguono due casi:
a)-il punto O appartiene alla retta r.
Sia r=AB la retta data e O un punto su di essa. E' noto che esiste la bisettrice di uno dei due angoli piatti di vertice O i cui lati OA e OB sono su una retta. Tale bisettrice b e la sua opposta formano la retta perpendicolare ad r. Siccome la bisettrice di un angolo è unica, tale è la perpendicolare alla retta AB in un punto O.

b)-Il punto O non appartiene alla retta r.

Corollario
Due rette perpendicolari alla stessa retta in due punti distinti non s'incontrano.
Infatti, se s'incontrassero in un punto, da questo si potrebbero condurre due perpendicolari distinte alla stessa retta.
Segmenti fra un punto ed una retta
In un piano si consideri una retta r ed un punto A non appartenente ad essa. Si conduca dal punto A la perpendicolare alla retta r e sia P il punto d'intersezione. Si congiunga A con un qualunque altro punto C di r, diverso da P.
Dicesi segmento di perpendicolare condotto da un punto A alla retta r, il segmento AP della perpendicolare alla retta compreso fra il punto e la retta stessa.
L'estremo P della perpendicolare alla retta si chiama piede della perpendicolare.
Ogni segmento che congiunge un punto dato A con un punto qualsiasi B di una retta, distinto da quello della perpendicolare, si dice linea obliqua, tale è il segmento AC. Il segmento AP prende il nome di distanza fra il punto A e la retta r.
Quindi, dicesi distanza del punto dalla retta, il segmento di perpendicolare abbassato dal punto alla retta.
In generale, dicesi distanza di un punto da una figura il più piccolo dei segmenti congiungente il punto con i punti della figura. Per distanza fra due punti s'intende il segmento che li unisce.

Proiezione di un punto sopra una retta
Se AP è il segmento di perpendicolare condotta dal punto A alla retta r e AC una qualsiasi linea obliqua, il segmento PC si dice proiezione del segmento AC sulla retta r. Quindi:
si chiama proiezione di un punto sopra una retta il piede della perpendicolare condotta dal punto alla retta.
Proiezione di un segmento sopra una retta
Si chiama proiezione di un segmento sopra una retta il segmento che ha per estremi le proiezioni dei due estremi.
La proiezione del segmento CD, che ha l'estremo C sulla retta r, è il segmento CD', essendo D' la proiezione del punto D.La proiezione del segmento AB sulla retta r è il segmento A'B', essendo A' e B' le proiezioni dei punti A e B.

Asse di un segmento
Dicesi asse di un segmento la retta perpendicolare al segmento condotta ad un segmento nel suo punto medio.
Si può verificare che che preso un qualsiasi punto P sull'asse del segmento AB, sono uguali le distanze del punto considerato dagli estremi del segmento, pertanto risulta: AP=PB.

Teorema - Se da un punto si conducono la perpendicolare e delle oblique ad una retta:
1)-il segmento di perpendicolare è minore di ogni obliqua;
2)-se due oblique hanno proiezioni uguali sono uguali;
3)-se due oblique hanno proiezioni disuguali è maggiore quella che ha proiezione maggiore. E viceversa.
Infatti, nel triangolo rettangolo POQ, OP è un cateto e OQ l'ipotenusa, quindi OP<OQ.
2)-Se le due oblique OQ, ON hanno uguali le proiezioni PQ e PN, si deve dimostrare che OQ e ON sono uguali. Infatti, i due triangoli OPQ e OPN hanno in comune il cateto OP ed hanno uguali i cateti PQ e PN per ipotesi; quindi sono uguali e tali sono le loro ipotenuse, cioè: OQ=ON, oblique date, come volevasi dimostrare.
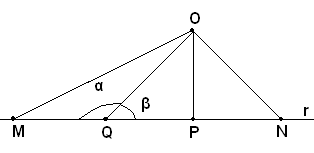
3)-Se le due oblique OM e ON hanno le loro rispettive proiezioni PM e PN disuguali, e precisamente se PM>PN, si deve dimostrare che OM>ON.
Infatti, se i segmenti OM e ON sono dalla parte opposta rispetto ad OP, si prende internamente a PM un segmento PQ=PN. L'angolo di vertice Q e lati QO E QM, α, è ottuso perchè adiacente all'angolo acuto di vertice Q e lati QP e QO, β; d'altronde nel triangolo ottusangolo OQM il lato OM>OQ=ON; quindi anche OM>ON.
Viceversa: Se OM=ON, i due triangoli rettangoli MPO e NPO risultano uguali perchè hanno l'ipotenusa e un cateto uguale, e quindi PM=PN. Se OM>ON, segue, per esclusione, che PM>PN.