MIKY & GENNY
TEOREMA DI TALETE E SIMILITUDINE ---> INDICE
Teorema
di Talete - Se un fascio di rette parallele è tagliato da due
trasversali, i segmenti determinati su una trasversale sono
direttamente proporzionali a quelli corrispondenti sull'altra.
Le rette parallele a, b, c, d tagliano le trasversali r ed r' rispettivamente nei punti A, B, C, D e A', B', C', D'; si deve dimostrare che:
(*) AB : CD = A'B' : C'D'.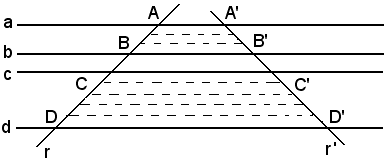
Si suppone prima che i segmenti AB e CD siano commensurabili, cioè si abbia, ad esempio, AB = 3/5CD. Si divide CD in 5 parti uguali e si riporta la quinta parte di CD su AB a partire da A; essa è contenuta esattamente tre volte in AB, perchè AB = 3/5CD. Ora per i punti di divisione di AB su CD si tracciano le parallele alle rette del fascio, in tal modo A'B' viene diviso in 3 parti uguali e C'D' in 5 parti uguali a quelle in cui è stato diviso A'B', perchè a segmenti uguali fra loro sulla trasversale r corrispondono segmenti uguali fra loro sulla trasversale r'. Quindi, si ha: A'B' = 3/5 C'D' e siccome anche AB = 3/5CD, i rapporti fra AB e CD e fra A'B' e C'D' sono entrambi uguali a 3/5, si ha:
AB : CD = A'B' : C'D'.
Siccome queste considerazioni si possono ripetere se al posto della frazione 3/5 si considera la frazione m/n qualsiasi, il teorema, nel caso in cui AB e CD siano commensurabili, è dimostrato.
Nota bene
(*) Le proporzioni da dimostrare potevano anche essere:
AC : AB = A'C' : A'B',
oppure
AC : BD = A'C' : B'D', ecc.
In ogni caso basta considerare su una trasversale due segmenti qualsiasi, anche parzialmente sovrapposti, e prendere sull'altra i segmenti corrispondenti.
Qualora i segmenti AB e CD siano incommensurabili, per dimostrare la proporzione
AB : CD = A'B' : C'D',
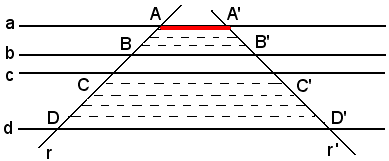
si applica il criterio di proporzionalità. Basta perciò far vedere che i valori per difetto del rapporto fra AB e CD sono anche valori per difetto del rapporto fra A'B' e C'D'.
Per questo si divide CD in un certo numero di parti uguali, per esempio 5, e si osserva che la quinta parte di CD è contenuta 3 volte in AB con un resto minore di un quinto, indicato in rosso nella figura suddetta. Ciò significa che 3/5CD<AB. Conducendo dai punti di divisione di CD e AB le parallele alle rette del fascio, C'D' resta diviso in 5 parti uguali fra loro ed A'B' in 3 parti uguali a quelle in cui è stato diviso C'D' più un resto minore di 1/5C'D'. Dunque risulta anche 3/5C'D'<A'B'. Le disuguaglianze 3/5CD<AB e 3/5C'D'<A'B' indicano che 3/5 è un valore approssimato per difetto tanto del rapporto fra AB e CD quanto di quello fra A'B' e C'D'. Siccome queste considerazioni possono ripetersi se al posto della frazione 3/5 si considera una frazione m/n qualsiasi, si può concludere che i rapporti:
AB : CD e A'B' : C'D'
hanno gli stessi valori per difetto e quindi che sono uguali, come volevasi dimostrare.
Teorema - Una retta parallela ad un lato di un triangolo, e che taglia gli altri due lati, determina su questi segmenti proporzionali.
Sia ABC un triangolo e la DE retta parallela al lato BC che taglia gli altri due lati nei punti D, E. Si deve dimostrare che:
AD : DB = AE : EC,
AD : AB = AE : AC.
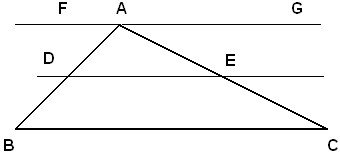
Infatti, conducendo per A la parallela FG a BC, si ha un fascio di rette parallele tagliate dalle trasversali AB, AC, quindi, per il teorema di Talete, si ricava:
AD : DB = AE : EC,
o anche
AD : AB = AE : AC.
Teorema - Se una retta stacca su due lati di un triangolo segmenti proporzionali, è parallela al terzo lato.
Sia ABC un triangolo e DE la retta che stacca sui lati AB, AC del triangolo segmenti proporzionali, cioè si abbia:
AD : BD = AE : EC,
Si deve dimostrare che: DE è parallela a BC.
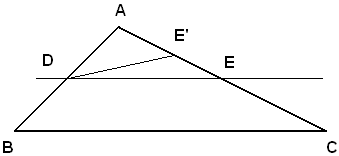
Infatti, ragionando per assurdo, se DE non fosse parallela a BC, conducendo DE' parallela a BC, si avrebbe:
(1) AB : AD = AC : DE',
e componendo la proporzione AD : BD = AE : EC, vera per ipotesi, si ricava:
(AD + BD) : AD = (AE + EC) : AE,
ossia
AB : AD = AC : AE.
Confrontando questa proporzione con la (1), risulta che AE ed AE', pur essendo disuguali, sarebbero entrambi quarti proporzionali dopo gli stessi 3 segmenti, e ciò è assurdo. Siccome l'assurdo è derivato dall'aver supposto che DE non fosse parallela a BC, si deve concludere che lo è.
Problema 1)- Costruire il quarto proporzionale dopo 3 segmenti dati.Siano a, b, c, tre segmenti; si vuole costruire un segmento x, tale che si abbia:
a : b = c : x.
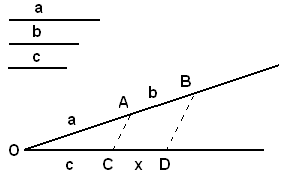
Si tracciano due semirette non opposte aventi la stessa origine O; su una di esse si prendono due segmenti consecutivi OA = a, AB = b; sull'altra, il segmento OC = C. Si congiunge A con C e si traccia da B la parallela ad AC e sia D il suo punto d'intersezione con la semiretta OC; si ha:
OA : AB = OC : CD,
ossia
a : b = c : CD,
quindi risulta
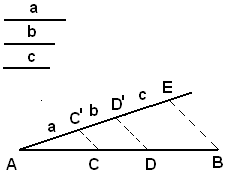
Dall'estremo A si traccia una semiretta e su questa, a partire da A, si riportano successivamente i segmenti AC' = a, C'D' = b, D'E = c. Si congiunge E con B, dai punti C, D' si traccia la parallela a questa retta. I punti d'incontro C, D di queste parallele col segmento AB sono i punti cercati.
Infatti, si ha:
AC : CD : DB = AC' : C'D' : D'E = a : b : c.
Teorema delle bisettrici di un triangolo - La bisettrice di un angolo di un triangolo divide il lato opposto in parti proporzionali agli altri due lati. La bisettrice di un angolo esterno, se incontra la retta del lato opposto, la interseca in un punto le cui distanze dagli estremi del lato sono proporzionali agli altri due lati.
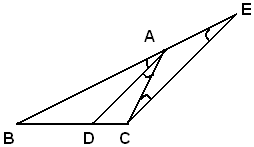
1)-Sia ABC un triangolo, AD la bisettrice relativa al lato BC. Si deve dimostrare che:
BD : DC = AB : AC.
Infatti, da C si traccia la parallela ad AD e sia E la sua intersezione con la retta BA. Per il teorema di Talete, si ha:
BD : DC = AB : AE.
D'altra parte
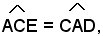
perchè alterni fra le parellele AD, CE e la trasversale AC, e
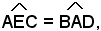
anche
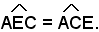
Il triangolo AEC risulta pertanto isoscele sulla base EC e quindi è AE = AC. Sostituendo AC ad AE nella proporzione precedente si ha:
BD : DC = AB : AC.
2)-Si suppone ora che la bisettrice AD' dell'angolo esterno di vertice A e lati AB, AE, incontri la retta del lato BC in un punto D'. Si deve dimostrare che:
D'B : D'C = AB : AC.
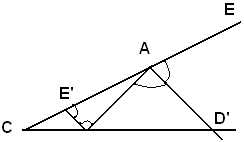
Infatti, da B si traccia la parallela alla retta AD' e sia E' la sua intersezione con la retta AC; si ha:
D'altra parte
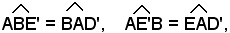
quindi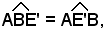
maAE' = AB,
dunque
D'B : D'C = AE' : AC.
Nota bene
La bisettrice dell'angolo esterno di un triangolo non incontra la retta del lato opposto nel caso in cui il triangolo sia isoscele con la base sul lato opposto.
Triangoli simili
Definizione - Due triangoli si dicono simili quando hanno i tre lati ordinatamente uguali ed i lati omologhi proporzionali.
Si dicono omologhi i lati dei due triangoli opposti ad angoli uguali.
Si dice rapporto di similitudine il rapporto di due lati omologhi.
Dalla definizione si ricava:
1)-La similitudine dei triangoli gode delle proprietà riflessiva, simmetrica e transitiva.
2)-Due triangoli uguali sono simili.
Per decidere della similitudine di due triangoli non occorre accertarsi, secondo quanto è stato detto nella definizione, dell'uguaglianza di tutti gli angoli e della proporzionalità di tutti i lati. Basta che sussistano alcune delle condizioni imposte dalla definizione affinchè le altre siano senz'altro verificate. Si hanno così i tre criteri di similitudine dei triangoli.
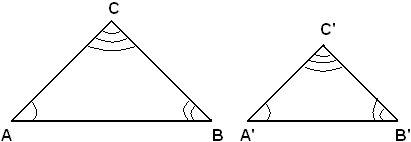
Primo criterio di similitudine dei triangoli
Se due triangoli hanno gli angoli ordinatamente uguali, hanno anche i lati omologhi proporzionali, cioè sono simili.
Siano ABC, A'B'C' due triangoli, α, β, γ gli angoli del primo ed α', β' γ' quelli del secondo e sia, per ipotesi:
α = α', β = β', γ = γ'.
Si deve dimostrare che:
AB : A'B' = AC : A'C' = BC : B'C'.
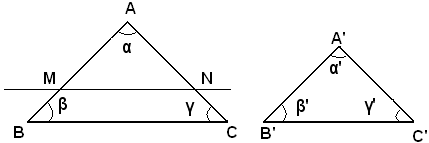
Infatti, se AB = A'B', i due triangoli sono uguali e quindi simili.
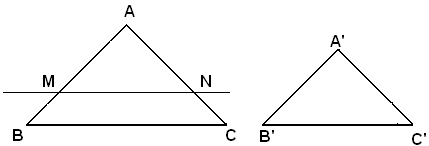
Supposto AB > A'B', sul lato AB si stacca un segmento AM = A'B' e si traccia la retta MN parallela a BC. Per il teorema di Talete, si ha:
AB : AM = AC : AN.
D'altra parte i due triangoli AMN, A'B'C' sono uguali perchè hanno i lati AM e A'B' uguali per costruzione, gli angoli α ed α' uguali per ipotesi e gli angoli di vertice M e lati MA, MN e di vertice B' e lati B'A' e B'C' anche uguali, perchè entrambi uguali all'angolo α.
Segue che:
AN = A'C'.
Sostituendo nella proporzione precedente A'B' ad AM e A'C' ad AN, si ha:
AB : A'B' = AC : A'C'.
Analogamente si dimostra che:
AB : A'B' = = BC : B'C';
dunque i due triangoli avendo gli angoli uguali e i lati proporzionali sono simili.
Secondo criterio di similitudine dei triangoli
Se due triangoli hanno un angolo uguale ed i lati omologhi proporzionali sono simili.
Siano ABC, A'B'C' due triangoli, e si abbia
α = α'
ed inoltre
AB : A'B' = AC : A'C'.
Si deve dimostrare che i due triangoli sono simili.
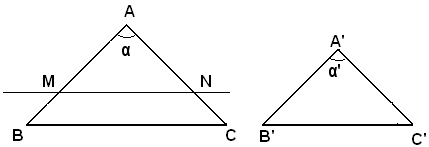
Infatti, se AB = A'B', dalla proporzione precedente, risulta AC = A'C' e perciò i due triangoli sono uguali per il primo criterio.
Supposto AB > A'B', sul lato AB si considera un segmento AM = A'B' e si traccia la retta MN parallela a BC; si ha:
AB : AM = AC : AN.
Confrontando questa proporzione con quella data dall'ipotesi, poichè AM = A'B', si ricava, per l'unicità del quarto proporzionale, AN = A'C'. I due triangoli AMN ed A'B'C' hanno così due lati uguali, ed uguale l'angolo compreso e quindi sono uguali. Siccome ABC è simile, per il primo criterio, ad MN, è anche simile a A'B'C'.
Si deve dimostrare che i due triangoli sono simili.
Infatti, se AB = A'B', siccome i lati dei triangoli sono proporzionali, si ha anche:
AC = A'C' e BC = B'C',
perciò i due triangoli sono uguali e quindi simili.
Supposto AB > A'B', sul lato AB si considera un segmento AM = A'B' e si traccia la retta MN parallela a BC. Dalla similitudine dei triangoli ABC, AMN, si ha:
AB : AM = AC : AN,
mentre per ipotesi è
AB : A'B' = AC : A'C'.
Confrontando quest'ultime due proporzioni, essendo AM = A'B', si ricava, per l'unicità del quarto proporzionale, AN =A'C'. Inoltre, sempre dalla similitudine dei triangoli ABC, AMN, si ha:
AB : AM = BC : MN,
mentre per ipotesi è
Confrontando quest'ultime due proporzioni, risulta che MN=B'C'. I due triangoli AMN, A'B'C' risultano dunque uguali e quindi simili, perchè hanno i tre lati uguali; e poichè ABC è simile ad AMN, per la proprietà transitiva, risulta anche simile ad A'B'C'.
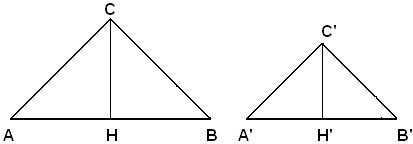
Teorema - In due triangoli simili le altezze condotte da due vertici omologhi sono proporzionali a due lati omologhi qualsiasi.
Nei due triangoli simili ABC, A'B'C, siano CH e C'H' due altezze condotte dai vertici omologhi C e C'. I triangoli ACH e A'C'H' sono simili perchè hanno l'angolo in A uguale all'angolo in A', per ipotesi, e l'angolo di vertice H e lati HC, HA uguale all'angolo di vertice H' e lati H'C', H'A', perchè retti; perciò si ha:
CH : C'H' = AB : A'B', ecc.
Nota bene
Per stabilire le proporzioni fra i lati di due triangoli simili, di cui si conoscono gli angoli corrispondenti, si procede così: trovate le coppie di lati omologhi, che sono quelli opposti agli angoli rispettivamente uguali, si pongono come termini di ogni rapporto due lati omologhi, come antecedenti i lati di uno dei triangoli e come conseguenti i lati dell'altro.
Ad esempio, nei triangoli simili ABC, BED, aventi coppie di angoli uguali, come è indicato in figura, sono omologhi i lati BC e BE, opposti agli angoli uguali in A e D, i lati AB e BD, opposti agli angoli uguali in C e in E e i lati AC e D, opposti all'angolo comune in B.
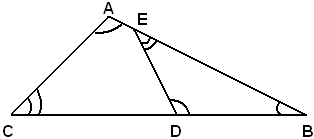
Sussistono dunque le seguenti proporzioni:
BC : BE = AB : BD = AC : DE.
In queste proporzioni, i termini di ogni rapporto sono due lati omologhi, gli antecedenti, BC, AB, AB, sono i lati del triangolo ABC ed i conseguenti, BE, BD, DE, sono i lati corrispondenti del triangolo BDE.
Nel caso di due triangoli simili con un lato in comune, questo dev'essere contato due volte: una prima volta come lato di uno dei triangoli, una seconda volta come lato dell'altro.
Applicazioni della similitudine dei triangoli
Primo teorema di Euclide
In un triangolo rettangolo, un cateto è medio proporzionale fra l'ipotenusa e la proiezione dello stesso sull'ipotenusa.
Sia ABC un triangolo rettangolo In A e BD la proiezione del cateto AB sull'ipotenusa BC. Si deve dimostrare che:
BC : AB = AB : BD.
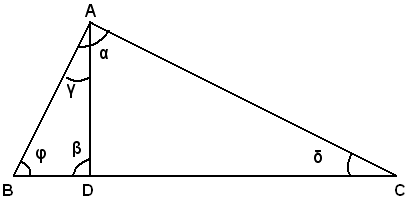
Infatti, i due triangoli ABC, BDA sono simili perchè hanno gli angoli α e β retti, l'angolo φ in comune e di conseguenza i restanti angoli γ e δ. Pertanto, essendo omologhi i lati BC e AB, opposti agli angoli retti, ed i lati AB, BD, opposti agli angoli uguali δ e γ, sussiste la proporzione:
BC : AB = AB : BD,
come volevasi dimostrare.
Corollario - In un triangolo rettangolo il quadrato costruito su un cateto è equivalente al rettangolo avente per dimensioni l'ipotenusa e la proiezione dello stesso sull'ipotenusa.
Secondo teorema di Euclide
In un triangolo rettangolo, l'altezza relativa all'ipotenusa è media proporzionale fra le proiezioni dei cateti sull'ipotenusa.
Sia ABC un triangolo rettangolo In A e AD l'altezza relativa all'ipotenusa BC. Si deve dimostrare che:
BD : AD = AD : DC.
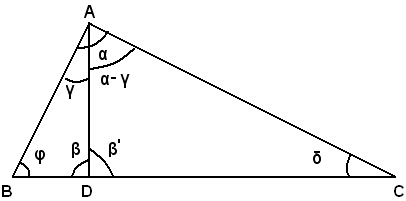
Infatti, i due triangoli DBA, DAC sono simili perchè hanno gli angoli β e β' uguali perchè retti, gli angoli γ e δ anche uguali in quanto complementari dello stesso angolo δ e di conseguenza i restanti angoli φ e α-γ. Pertanto, essendo omologhi i lati BD e AD, opposti agli angoli uguali γ e δ. ed i lati AD, DC, opposti agli angoli uguali φ e α-γ, sussiste la proporzione:
BD : AD = AD : DC,
come volevasi dimostrare
Corollario - In un triangolo rettangolo, il quadrato costruito sull'altezza relativa all'ipotenusa è equivalente al rettangolo avente per dimensioni le proiezioni dei cateti sull'ipotenusa.
Teorema delle corde
Se due corde di un cerchio si tagliano, le parti in cui si dividono formano una proporzione nella quale i medi sono le parti in cui è stata divisa una corda e gli estremi le parti in cui è divisa l'altra.
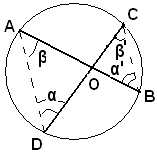
Due corde AB e CD di una circonferenza s'incontrano in un punto O. Si deve dimostrare che:
AO : OC = OD : OB.
Infatti, i triangoli AOD e COB sono simili in quanto hanno gli angoli α ed α' uguali perchè angoli alla circonferenza che insistono sullo stesso arco e gli angoli β e β' pure uguali perchè angoli alla circonferenza che insistono sullo stesso arco
e gli angoli β e β' pure uguali perchè angoli alla circonferenza che insistono sullo stesso arco  Pertanto, essendo omologhi AO e OC, opposti agli angoli uguali α ed α', ed OD e OB, opposti agli angoli uguali β e β', sussiste la seguente proporzione:
Pertanto, essendo omologhi AO e OC, opposti agli angoli uguali α ed α', ed OD e OB, opposti agli angoli uguali β e β', sussiste la seguente proporzione:
AO : OC = OD : OB,
come volevasi dimostrare.
Corollario - Se due corde di un cerchio si tagliano, sono equivalenti i rettangoli dei segmenti in cui ciascuna di esse è divisa dall'altra.
Teorema delle secanti
Se da un punto esterno ad una circonferenza si conducono due secanti, le intere secanti e le loro parti esterne formano una proporzione nella quale sono medi ed estremi le intere secanti e le loro parti esterne.
Da un punto esterno ad una circonferenza si tracciano due secanti OA, OC e siano OB e OD le loro rispettive parti esterne. Si deve dimostrare che:
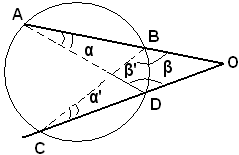
Infatti, si congiungono i punti A e D ed i punti B e C: i triangoli ODA e OBC sono simili in quanto hanno l'angolo in O in comune ed uguali gli angoli α ed α' come angoli alla circonferenza che insistono sullo stesso arco Pertanto risultano uguali gli angoli rimanenti β e β'. Essendo omologhi i lati OA ed OC, opposti agli angoli uguali β e β', e OD e OB, opposti agli angoli uguali in A ed in C, sussiste la proporzione:
Pertanto risultano uguali gli angoli rimanenti β e β'. Essendo omologhi i lati OA ed OC, opposti agli angoli uguali β e β', e OD e OB, opposti agli angoli uguali in A ed in C, sussiste la proporzione:
OA : OC = OD : OB.
Corollario - Se da un punto esterno si conducono due secanti ad un cerchio, sono equivalenti i rettangoli di ciascuna di esse e della relativa parte esterna.
Teorema della tangente
Se da un punto esterno si conducono una tangente ed una secante ad un cerchio, la tangente è media proporzionale fra l'intera secante e la sua parte esterna.
Siano PT la tangente, PB e PA l'intera secante e la sua parte esterna. Si deve dimostrare che:
PA : PT = PT : PB.
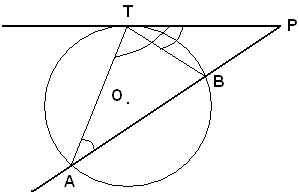
Infatti, i due triangoli PTA, PBT sono simili in quanto hanno l'angolo in P in comune, l'angolo in T e lati TP, TB uguale all'angolo in A e lati AP, AT come angoli alla circonferenza che insistono sullo stesso arco (l'angolo di vertice T e lati TP, TB ha il lato TP tangente) e l'angolo
di vertice T e lati TP, TA uguale all'angolo in B e lati BP, BT di conseguenza. Pertanto, essendo omologhi i lati PA e PT, opposti agli angoli uguali di vertice T e lati TP, TA e di vertice in B e lati BP, BT, e i lati PT e PB, opposti agli angoli uguali in A e di vertice T e lati TP, TB, sussiste la proporzione:
(l'angolo di vertice T e lati TP, TB ha il lato TP tangente) e l'angolo
di vertice T e lati TP, TA uguale all'angolo in B e lati BP, BT di conseguenza. Pertanto, essendo omologhi i lati PA e PT, opposti agli angoli uguali di vertice T e lati TP, TA e di vertice in B e lati BP, BT, e i lati PT e PB, opposti agli angoli uguali in A e di vertice T e lati TP, TB, sussiste la proporzione:
PA : PT = PT : PB,
come volevasi dimostrare.
Corollario - Se da un punto esterno si conducono una tangente ed una secante ad un cerchio, il quadrato costruito sulla tangente è equivalente al rettangolo dell'intera secante e della parte esterna.
Costruzione del medio proporzionale
Costruire il segmento medio proporzionale fra due segmenti dati.
1° Modo: siano a e b due segmenti su una retta OA, da bande opposte rispetto ad un punto O, si costruiscono i segmenti OA = a, OB = b. Si descrive una semicirconferenza avente per diametro AB e sia C il punto in cui la perpendicolare da O ad OB incontra tale semicirconferenza.
Si deve dimostrare che OC è il segmento medio proporzionale fra OA e OB, ossia fra a e b.
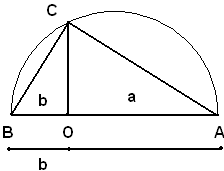
Infatti, si congiunge C con A e con B, essendo il rettangolo ABC rettangolo in C, per il secondo teorema di Euclide, si ha:
OA : OC = OC : OB.
2° Modo: siano a e b due segmenti su una retta OA, da una stessa banda rispetto ad un punto O, si costruiscono i segmenti OA = a, OB = b. Se OA> OB, si descrive una semicirconferenza avente per diametro OA. Sia C il punto in cui la perpendicolare da B ad OB incontra tale semicirconferenza.
Si deve dimostrare che OC è il segmento medio proporzionale fra OA e OB, ossia fra a e b.
Infatti, si congiunge C con O e con A, essendo il rettangolo OCA rettangolo in C, perchè inscritto nella semicirconferenza, per il primo teorema di Euclide, si ha:
OA : OC = OC : OB.
Parte aurea di un segmento
Definizione - Si chiama parte aurea di un segmento quella parte che è media proporzionale fra l'intero segmento e la parte rimanente,
Costruzione della parte aurea di un segmento
Sia assegnato un segmento AB; dall'estremo B si conduce la perpendicolare ad AB e su di essa si considera un segmento BO uguale alla metà di AB. Puntando nel centro O e con raggio uguale ad OB, si descrive una circonferenza; essa risulta tangente ad AB in B. Si congiunge A con O e sia C il punto in cui il segmento OA incontra la circonferenza. Costruito AD = AC, si deve dimostrare che: AD è la parte aurea del segmento AB.
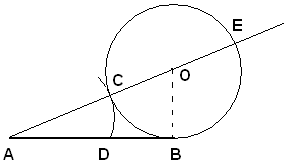
Infatti, prolungando AO fino ad incontrare in E la circonferenza, per il teorema della tangente si ha:
AE : AB = AB : AC
e dividendo
(AE - AB) : AB = (AB - AC) : AC.
Essendo
AB = CE e AC = AD,
si ha:
AE - AB = AE - CE = AC = AD
e
AB - AC = AB - AD = DB.
Dunque la proporzione precedente si può scrivere:
AD : AB = DB : AD
e invertendo, si ha
AB : AD = AD : DB.
Quindi AD è la parte aurea di AB.
Nota bene
Un segmento che è diviso in due parti di cui una sia la parte aurea, si dice che è diviso in media ed estrema ragione.
Costruzione del decagono regolare
Teorema - Il lato del decagono regolare inscritto in un cerchio è uguale alla parte aurea del raggio del cerchio stesso.
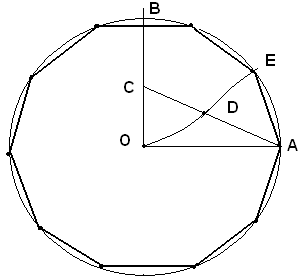
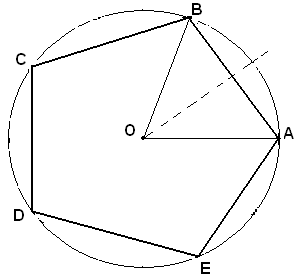
Siano OA, OB i raggi di un cerchio di centro O ed AB il lato del decagono regolare in esso inscritto.
Si deve dimostrare che AB è la parte aurea di OA.
Nel triangolo isoscele AOB l'angolo in O, essendo la decima parte dell'angolo giro, è 1/5 di un angolo piatto e allora ciascuno degli angoli uguali di vertice A e lati AO, AB e di vertice B e lati BO, BA è 2/5 di un angolo piatto. Perciò, se si traccia la bisettrice BC, gli angoli di vertice B e lati BO, BC e di vertice B e lati BC, BA sono ciascuno 1/5 di un angolo piatto, cioè uguali all'angolo in O. Si deduce che il triangolo OBC risulta isoscele sulla base OB. Inoltre, essendo l'angolo in C e lati CB, CA uguale a 2/5 di un angolo piatto, esso risulta uguale all'angolo di vertice A e lati AB, AC e allora il triangolo ABC risulta isoscele sulla base AC. Segue quindi che OC = BC, come lati del triangolo isoscele OCB e BC = AB, come lati del triangolo isoscele ABC. Da queste due uguaglianze, si ricava OC = AB. D'altra parte, dai triangoli simili OAB e BAC, si ha:
OA : AB = AB : CA
e ponendo, per l'uguaglianza precedente, OC al posto di AB, si ottiene:
OA : OC = OC : CA.
Da questa importante proporzione risulta che OC è uguale alla parte aurea del raggio; quindi anche AB, uguale al lato del decagono regolare, è uguale alla parte aurea del raggio.
La costruzione del decagono regolare inscritto in un cerchio risulta senz'altro da questo teorema.
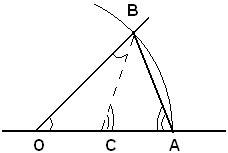
Si conduce per O il raggio OB perpendicolare al raggio OA del cerchio dato e, diviso OB in due parti uguali mediante il punto C, si congiunge A con C. Puntando in C, e raggio CO, si descrive un arco di cerchio in modo che tagli AC in D. AD è uguale alla sezione aurea del raggio e quindi al lato del decagono regolare.
Costruzione del pentagono regolare
Poligoni simili
Definizione - Due poligoni si dicono simili se hanno gli angoli ordinatamente uguali e i lati omologhi proporzionali.
Si chiamano omologhi i lati di due poligoni simili che hanno come estremi i vertici di angoli uguali.
Si dice rapporto di similitudine il rapporto fra due lati omologhi qualsiasi.
Dalla definizione si ricava:
1)-la similitudine fra due poligoni gode della proprietà riflessiva, simmetrica e transitiva.
2)-i poligoni regolari dello stesso numero di lati sono simili.
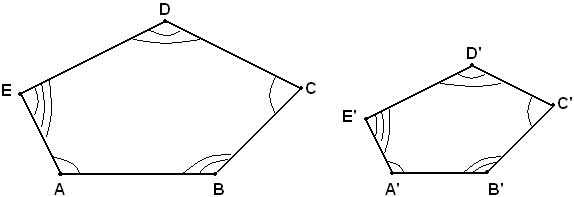
Teorema - Se in due poligoni simili da due vertici corrispondenti si conducono tutte le possibili diagonali, i poligoni restano divisi nello stesso numero di triangoli ordinatamente simili.
Siano ABCDE, A'B'C'D'E' i poligoni simili e si abbia:

ed inoltre
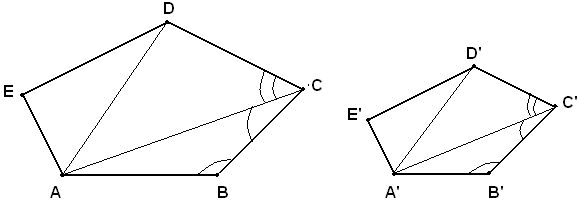
Infatti, i triangoli ABC, A'B'C' sono simili, perchè hanno gli angoli in B e in B' uguali e i lati AB, BC e A'B' B'C', che li comprendono, proporzionali. Segue quindi:
(1) BC : B'C' = AC : A'C'
e che
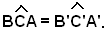
Si tiene conto ora che, per ipotesi risulta:
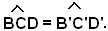
QuindI, sottraendo membro a membro questa uguaglianza dalla precedente, si ha:
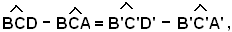
ossia
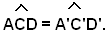
Inoltre, poichè per ipotesi risuta ancora:
BC : B'C' = CD : C'D',
confrontando questa proporzione con la (1), si vede che le due proporzioni hanno i primi due rapporti uguali; quindi gli altri due rapporti formano la proporzione
AC = A'C' = CD : C'D'.
I due triangoli ACD, A'C'D' sono quindi simili, perchè hanno un angolo uguale
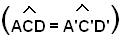
e i lati che lo comprendono in proporzione.
Analogamente si dimostra che sono simili gli altri triangoli.
Teorema - I perimetri di due poligoni simili stanno fra loro come due lati corrispondenti qualsiasi.
Siano ABCDE, A'B'C'D'E' due poligoni simili di perimetri P e P'. Si deve dimostrare che:
P : P' = AB : A'B'.
Infatti, nella figura precedente, per la similitudine dei poligoni, si ha:
AB : A'B' = BC : B'C' = .... = EA : E'A',
e da questa catena di rapporti si ricava
(AB + BC + CD + DE. + EA) : (A'B' + B'C' + C'D' + D'E' + E'A') = AB : A'B',
ossia
P : P' = AB : A'B'.
come volevasi dimostrare.
Teorema - Due poligoni simili stanno fra loro come i quadrati di due lati corrispondenti.
1)-Si dimostra il teorema nel caso dei triangoli.
Siano ABC, A'B'C' due triangoli simili, si deve dimostrare che:
∆ABC : ∆A'B'C' = q(AB) : q(A'B').
Infatti, indicando con a e a' le misure dei due lati corrispondenti AB, A'B', con h e h' le misure delle relative altezze e con S, S' le misure dei triangoli, cioè le loro aree, si ha:
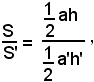
ossia (1)
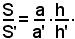
Inoltre, per il teorema dimostrato in precedenza "in due triangoli simili le altezze condotte da due vertici omologhi sono proporzionali a due lati omologhi qualsiasi", si ha:
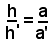
e, sostituendo in (1) al rapporto
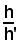
il valore precedente, si ha:
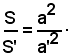
E' così dimostrato che le aree dei triangoli, e quindi i triangoli stessi, stanno come i quadrati dei loro due lati corrispondenti.
2)-Si dimostra il teorema nel caso generale di due poligoni.
Siano dati i due poligoni ABCDE, A'B'C'D'E'
Si deve dimostrare che:
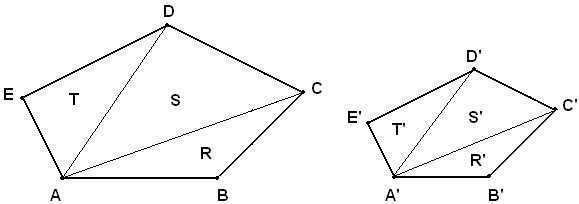
Infatti, se da due vertici corrispondenti, A, A' si tracciano tutte le possibili diagonali, i due poligoni vengono scomposti nello stesso numero di triangoli ordinatamente simili. Si indicano con R, S, T, i triangoli nei quali viene scomposto il primo poligono e con R', S', T' quelli in cui viene scomposto il secondo. Per la prima parte di questo teorema, si ha:
R : R' = q(AC) : q(A'C')
e
S : S' = q(AC) : q(A'C').
Per il teorema dimostrato in precedenza "due coppie di grandezze proporzionali ad una terza sono proporzionali fra loro", si ha:
R : R' = S : S'.
Analogamente si dimostra che
S : S' = T : T'.
Tenendo conto delle due proporzioni precedenti:
R : R' = S : S' = T : T'
ed ancora si ha:
(R + S + T) : (R' + S' + T') = R : R',
ossia
ABCDE : A'B'C'D'E' = R : R'
ma essendo:
R : R' = q(AB) : q(A'B'),
si conclude perciò che:
ABCDE : A'B'C'D'E' = q(AB) : q(A'B').
Teorema - I perimetri di due poligoni regolari dello stesso numero di lati stanno fra loro come i lati, come i raggi, come gli apotemi.
Siano ABCDE, A'B'C'D'E' due poligoni regolari dello stesso numero di lati, ad esempio 5, OH e O'H' gli apotemi, OA e O'A' i raggi, P, P' i perimetri.
Si deve dimostrare che:
P : P' = AB : A'B' = OA : O'A' = OH: O'H'.
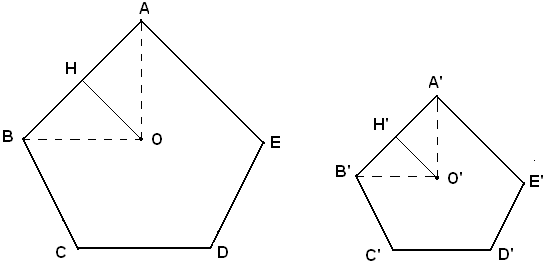
Infatti, due poligoni regolari, aventi lo stesso numero di lati, essendo simili, si ha:
P : P' = AB : A'B'.
Inoltre i due triangoli OAH, O'A'H' sono simili perchè sono rettangoli ed hanno gli angoli acuti in O, O' uguali in quanto metà di angoli uguali; perciò si ha:
AH : A'H' = OA : O'A' = OH : O'H'
e raddoppiando i termini del primo rapporto:
AB : A'B' = OA : O'A' = OH: O'H',
cioè i lati stanno fra loro come i raggi e come gli apotemi e, siccome i perimetri stanno fra loro come i lati, il teorema è dimostrato.
Teorema - Due poligoni regolari dello stesso numero di lati stanno fra loro come i quadrati dei lati omologhi, dei raggi, degli apotemi.
Siano S ed S' due poligoni regolari, di cui AB, A'B' siano due lati, OA e O'A' due raggi ed OH, O'H' i due apotemi, fra loro corrispondenti. Per il teorema "due poligoni simili stanno fra loro come i quadrati dei lati corrispondenti", si ha.
S : S' = q(AB) : q(A'B').
Siccome per il teorema precedente:
AB : A'B' = OA : O'A' = OH: O'H',
anche i quadrati di questi segmenti sono in proporzione, cioè:
q(AB) : q(A'B') = q(OA) : q(O'A') = q(OH) : q(O'H'),
Tenendo conto della proporzione (1), si può concludere che:
S : S' = q(OA) : q(O'A') = q(OH) : q(O'H'),
come volevasi dimostrare.
Le rette parallele a, b, c, d tagliano le trasversali r ed r' rispettivamente nei punti A, B, C, D e A', B', C', D'; si deve dimostrare che:

Si suppone prima che i segmenti AB e CD siano commensurabili, cioè si abbia, ad esempio, AB = 3/5CD. Si divide CD in 5 parti uguali e si riporta la quinta parte di CD su AB a partire da A; essa è contenuta esattamente tre volte in AB, perchè AB = 3/5CD. Ora per i punti di divisione di AB su CD si tracciano le parallele alle rette del fascio, in tal modo A'B' viene diviso in 3 parti uguali e C'D' in 5 parti uguali a quelle in cui è stato diviso A'B', perchè a segmenti uguali fra loro sulla trasversale r corrispondono segmenti uguali fra loro sulla trasversale r'. Quindi, si ha: A'B' = 3/5 C'D' e siccome anche AB = 3/5CD, i rapporti fra AB e CD e fra A'B' e C'D' sono entrambi uguali a 3/5, si ha:
AB : CD = A'B' : C'D'.
Siccome queste considerazioni si possono ripetere se al posto della frazione 3/5 si considera la frazione m/n qualsiasi, il teorema, nel caso in cui AB e CD siano commensurabili, è dimostrato.
Nota bene
(*) Le proporzioni da dimostrare potevano anche essere:
oppure
In ogni caso basta considerare su una trasversale due segmenti qualsiasi, anche parzialmente sovrapposti, e prendere sull'altra i segmenti corrispondenti.
Qualora i segmenti AB e CD siano incommensurabili, per dimostrare la proporzione
AB : CD = A'B' : C'D',

si applica il criterio di proporzionalità. Basta perciò far vedere che i valori per difetto del rapporto fra AB e CD sono anche valori per difetto del rapporto fra A'B' e C'D'.
Per questo si divide CD in un certo numero di parti uguali, per esempio 5, e si osserva che la quinta parte di CD è contenuta 3 volte in AB con un resto minore di un quinto, indicato in rosso nella figura suddetta. Ciò significa che 3/5CD<AB. Conducendo dai punti di divisione di CD e AB le parallele alle rette del fascio, C'D' resta diviso in 5 parti uguali fra loro ed A'B' in 3 parti uguali a quelle in cui è stato diviso C'D' più un resto minore di 1/5C'D'. Dunque risulta anche 3/5C'D'<A'B'. Le disuguaglianze 3/5CD<AB e 3/5C'D'<A'B' indicano che 3/5 è un valore approssimato per difetto tanto del rapporto fra AB e CD quanto di quello fra A'B' e C'D'. Siccome queste considerazioni possono ripetersi se al posto della frazione 3/5 si considera una frazione m/n qualsiasi, si può concludere che i rapporti:
AB : CD e A'B' : C'D'
hanno gli stessi valori per difetto e quindi che sono uguali, come volevasi dimostrare.
Teorema - Una retta parallela ad un lato di un triangolo, e che taglia gli altri due lati, determina su questi segmenti proporzionali.
Sia ABC un triangolo e la DE retta parallela al lato BC che taglia gli altri due lati nei punti D, E. Si deve dimostrare che:
AD : DB = AE : EC,
AD : AB = AE : AC.

Infatti, conducendo per A la parallela FG a BC, si ha un fascio di rette parallele tagliate dalle trasversali AB, AC, quindi, per il teorema di Talete, si ricava:
o anche
Teorema - Se una retta stacca su due lati di un triangolo segmenti proporzionali, è parallela al terzo lato.
Sia ABC un triangolo e DE la retta che stacca sui lati AB, AC del triangolo segmenti proporzionali, cioè si abbia:
Si deve dimostrare che: DE è parallela a BC.

Infatti, ragionando per assurdo, se DE non fosse parallela a BC, conducendo DE' parallela a BC, si avrebbe:
(1) AB : AD = AC : DE',
e componendo la proporzione AD : BD = AE : EC, vera per ipotesi, si ricava:
ossia
Confrontando questa proporzione con la (1), risulta che AE ed AE', pur essendo disuguali, sarebbero entrambi quarti proporzionali dopo gli stessi 3 segmenti, e ciò è assurdo. Siccome l'assurdo è derivato dall'aver supposto che DE non fosse parallela a BC, si deve concludere che lo è.
Problema 1)- Costruire il quarto proporzionale dopo 3 segmenti dati.

Si tracciano due semirette non opposte aventi la stessa origine O; su una di esse si prendono due segmenti consecutivi OA = a, AB = b; sull'altra, il segmento OC = C. Si congiunge A con C e si traccia da B la parallela ad AC e sia D il suo punto d'intersezione con la semiretta OC; si ha:
ossia
a : b = c : CD,
quindi risulta
CD = x.
Si noti che, per l'unicità del quarto proporzionale, il segmento CD è unico, qualunque sia la costruzione che si esegue.
Nota bene
Se b = c, la stessa costruzione fornisce il terzo proporzionale dopo due segmenti dati.
Problema 2)- Dividere un segmento in parti proporzionali a più segmenti dati.
Siano a, b, c tre segmenti; si vuole dividere un segmento AB in parti proporzionali ad essi.
Si noti che, per l'unicità del quarto proporzionale, il segmento CD è unico, qualunque sia la costruzione che si esegue.
Nota bene
Se b = c, la stessa costruzione fornisce il terzo proporzionale dopo due segmenti dati.
Problema 2)- Dividere un segmento in parti proporzionali a più segmenti dati.
Siano a, b, c tre segmenti; si vuole dividere un segmento AB in parti proporzionali ad essi.

Dall'estremo A si traccia una semiretta e su questa, a partire da A, si riportano successivamente i segmenti AC' = a, C'D' = b, D'E = c. Si congiunge E con B, dai punti C, D' si traccia la parallela a questa retta. I punti d'incontro C, D di queste parallele col segmento AB sono i punti cercati.
Infatti, si ha:
AC : CD : DB = AC' : C'D' : D'E = a : b : c.
Teorema delle bisettrici di un triangolo - La bisettrice di un angolo di un triangolo divide il lato opposto in parti proporzionali agli altri due lati. La bisettrice di un angolo esterno, se incontra la retta del lato opposto, la interseca in un punto le cui distanze dagli estremi del lato sono proporzionali agli altri due lati.
1)-Sia ABC un triangolo, AD la bisettrice relativa al lato BC. Si deve dimostrare che:
BD : DC = AB : AC.
Infatti, da C si traccia la parallela ad AD e sia E la sua intersezione con la retta BA. Per il teorema di Talete, si ha:

D'altra parte
perchè alterni fra le parellele AD, CE e la trasversale AC, e
perchè corrispondenti fra le parellele AD, CE e la trasversale BE, ed essendo per ipotesi
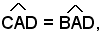
anche
Il triangolo AEC risulta pertanto isoscele sulla base EC e quindi è AE = AC. Sostituendo AC ad AE nella proporzione precedente si ha:
2)-Si suppone ora che la bisettrice AD' dell'angolo esterno di vertice A e lati AB, AE, incontri la retta del lato BC in un punto D'. Si deve dimostrare che:

Infatti, da B si traccia la parallela alla retta AD' e sia E' la sua intersezione con la retta AC; si ha:
D'B : D'C = AE' : AC.
D'altra parte
quindi
ma
dunque
D'B : D'C = AE' : AC.
Nota bene
La bisettrice dell'angolo esterno di un triangolo non incontra la retta del lato opposto nel caso in cui il triangolo sia isoscele con la base sul lato opposto.
Triangoli simili
Definizione - Due triangoli si dicono simili quando hanno i tre lati ordinatamente uguali ed i lati omologhi proporzionali.
Si dicono omologhi i lati dei due triangoli opposti ad angoli uguali.
Si dice rapporto di similitudine il rapporto di due lati omologhi.

Dalla definizione si ricava:
1)-La similitudine dei triangoli gode delle proprietà riflessiva, simmetrica e transitiva.
2)-Due triangoli uguali sono simili.
Per decidere della similitudine di due triangoli non occorre accertarsi, secondo quanto è stato detto nella definizione, dell'uguaglianza di tutti gli angoli e della proporzionalità di tutti i lati. Basta che sussistano alcune delle condizioni imposte dalla definizione affinchè le altre siano senz'altro verificate. Si hanno così i tre criteri di similitudine dei triangoli.
Primo criterio di similitudine dei triangoli
Se due triangoli hanno gli angoli ordinatamente uguali, hanno anche i lati omologhi proporzionali, cioè sono simili.
Siano ABC, A'B'C' due triangoli, α, β, γ gli angoli del primo ed α', β' γ' quelli del secondo e sia, per ipotesi:
Si deve dimostrare che:

Infatti, se AB = A'B', i due triangoli sono uguali e quindi simili.
Supposto AB > A'B', sul lato AB si stacca un segmento AM = A'B' e si traccia la retta MN parallela a BC. Per il teorema di Talete, si ha:
D'altra parte i due triangoli AMN, A'B'C' sono uguali perchè hanno i lati AM e A'B' uguali per costruzione, gli angoli α ed α' uguali per ipotesi e gli angoli di vertice M e lati MA, MN e di vertice B' e lati B'A' e B'C' anche uguali, perchè entrambi uguali all'angolo α.
Segue che:
Sostituendo nella proporzione precedente A'B' ad AM e A'C' ad AN, si ha:
Analogamente si dimostra che:
AB : A'B' = = BC : B'C';
dunque i due triangoli avendo gli angoli uguali e i lati proporzionali sono simili.
Secondo criterio di similitudine dei triangoli
Se due triangoli hanno un angolo uguale ed i lati omologhi proporzionali sono simili.
Siano ABC, A'B'C' due triangoli, e si abbia
ed inoltre
Si deve dimostrare che i due triangoli sono simili.

Infatti, se AB = A'B', dalla proporzione precedente, risulta AC = A'C' e perciò i due triangoli sono uguali per il primo criterio.
Supposto AB > A'B', sul lato AB si considera un segmento AM = A'B' e si traccia la retta MN parallela a BC; si ha:
Confrontando questa proporzione con quella data dall'ipotesi, poichè AM = A'B', si ricava, per l'unicità del quarto proporzionale, AN = A'C'. I due triangoli AMN ed A'B'C' hanno così due lati uguali, ed uguale l'angolo compreso e quindi sono uguali. Siccome ABC è simile, per il primo criterio, ad MN, è anche simile a A'B'C'.
Terzo criterio di similitudine dei triangoli
Se due triangoli hanno i lati proporzionali sono simili.
Siano ABC, A'B'C' due triangoli, e si abbia:
Se due triangoli hanno i lati proporzionali sono simili.
Siano ABC, A'B'C' due triangoli, e si abbia:
AB : A'B' = AC : A'C' = BC : B'C'.
Si deve dimostrare che i due triangoli sono simili.
Infatti, se AB = A'B', siccome i lati dei triangoli sono proporzionali, si ha anche:
AC = A'C' e BC = B'C',

perciò i due triangoli sono uguali e quindi simili.
Supposto AB > A'B', sul lato AB si considera un segmento AM = A'B' e si traccia la retta MN parallela a BC. Dalla similitudine dei triangoli ABC, AMN, si ha:
mentre per ipotesi è
Confrontando quest'ultime due proporzioni, essendo AM = A'B', si ricava, per l'unicità del quarto proporzionale, AN =A'C'. Inoltre, sempre dalla similitudine dei triangoli ABC, AMN, si ha:
AB : AM = BC : MN,
mentre per ipotesi è
AB : A'B' = AC : A'C'.
Confrontando quest'ultime due proporzioni, risulta che MN=B'C'. I due triangoli AMN, A'B'C' risultano dunque uguali e quindi simili, perchè hanno i tre lati uguali; e poichè ABC è simile ad AMN, per la proprietà transitiva, risulta anche simile ad A'B'C'.
Teorema - In due triangoli simili le altezze condotte da due vertici omologhi sono proporzionali a due lati omologhi qualsiasi.
Nei due triangoli simili ABC, A'B'C, siano CH e C'H' due altezze condotte dai vertici omologhi C e C'. I triangoli ACH e A'C'H' sono simili perchè hanno l'angolo in A uguale all'angolo in A', per ipotesi, e l'angolo di vertice H e lati HC, HA uguale all'angolo di vertice H' e lati H'C', H'A', perchè retti; perciò si ha:
CH : C'H' = AB : A'B', ecc.

Nota bene
Per stabilire le proporzioni fra i lati di due triangoli simili, di cui si conoscono gli angoli corrispondenti, si procede così: trovate le coppie di lati omologhi, che sono quelli opposti agli angoli rispettivamente uguali, si pongono come termini di ogni rapporto due lati omologhi, come antecedenti i lati di uno dei triangoli e come conseguenti i lati dell'altro.
Ad esempio, nei triangoli simili ABC, BED, aventi coppie di angoli uguali, come è indicato in figura, sono omologhi i lati BC e BE, opposti agli angoli uguali in A e D, i lati AB e BD, opposti agli angoli uguali in C e in E e i lati AC e D, opposti all'angolo comune in B.

Sussistono dunque le seguenti proporzioni:
BC : BE = AB : BD = AC : DE.
In queste proporzioni, i termini di ogni rapporto sono due lati omologhi, gli antecedenti, BC, AB, AB, sono i lati del triangolo ABC ed i conseguenti, BE, BD, DE, sono i lati corrispondenti del triangolo BDE.
Nel caso di due triangoli simili con un lato in comune, questo dev'essere contato due volte: una prima volta come lato di uno dei triangoli, una seconda volta come lato dell'altro.
Applicazioni della similitudine dei triangoli
Primo teorema di Euclide
In un triangolo rettangolo, un cateto è medio proporzionale fra l'ipotenusa e la proiezione dello stesso sull'ipotenusa.
Sia ABC un triangolo rettangolo In A e BD la proiezione del cateto AB sull'ipotenusa BC. Si deve dimostrare che:

Infatti, i due triangoli ABC, BDA sono simili perchè hanno gli angoli α e β retti, l'angolo φ in comune e di conseguenza i restanti angoli γ e δ. Pertanto, essendo omologhi i lati BC e AB, opposti agli angoli retti, ed i lati AB, BD, opposti agli angoli uguali δ e γ, sussiste la proporzione:
come volevasi dimostrare.
Corollario - In un triangolo rettangolo il quadrato costruito su un cateto è equivalente al rettangolo avente per dimensioni l'ipotenusa e la proiezione dello stesso sull'ipotenusa.
Secondo teorema di Euclide
In un triangolo rettangolo, l'altezza relativa all'ipotenusa è media proporzionale fra le proiezioni dei cateti sull'ipotenusa.
Sia ABC un triangolo rettangolo In A e AD l'altezza relativa all'ipotenusa BC. Si deve dimostrare che:

Infatti, i due triangoli DBA, DAC sono simili perchè hanno gli angoli β e β' uguali perchè retti, gli angoli γ e δ anche uguali in quanto complementari dello stesso angolo δ e di conseguenza i restanti angoli φ e α-γ. Pertanto, essendo omologhi i lati BD e AD, opposti agli angoli uguali γ e δ. ed i lati AD, DC, opposti agli angoli uguali φ e α-γ, sussiste la proporzione:
come volevasi dimostrare
Corollario - In un triangolo rettangolo, il quadrato costruito sull'altezza relativa all'ipotenusa è equivalente al rettangolo avente per dimensioni le proiezioni dei cateti sull'ipotenusa.
Teorema delle corde
Se due corde di un cerchio si tagliano, le parti in cui si dividono formano una proporzione nella quale i medi sono le parti in cui è stata divisa una corda e gli estremi le parti in cui è divisa l'altra.

Due corde AB e CD di una circonferenza s'incontrano in un punto O. Si deve dimostrare che:
AO : OC = OD : OB.
Infatti, i triangoli AOD e COB sono simili in quanto hanno gli angoli α ed α' uguali perchè angoli alla circonferenza che insistono sullo stesso arco
AO : OC = OD : OB,
come volevasi dimostrare.
Corollario - Se due corde di un cerchio si tagliano, sono equivalenti i rettangoli dei segmenti in cui ciascuna di esse è divisa dall'altra.
Teorema delle secanti
Se da un punto esterno ad una circonferenza si conducono due secanti, le intere secanti e le loro parti esterne formano una proporzione nella quale sono medi ed estremi le intere secanti e le loro parti esterne.
Da un punto esterno ad una circonferenza si tracciano due secanti OA, OC e siano OB e OD le loro rispettive parti esterne. Si deve dimostrare che:
OA : OC = OD : OB.

Infatti, si congiungono i punti A e D ed i punti B e C: i triangoli ODA e OBC sono simili in quanto hanno l'angolo in O in comune ed uguali gli angoli α ed α' come angoli alla circonferenza che insistono sullo stesso arco
Corollario - Se da un punto esterno si conducono due secanti ad un cerchio, sono equivalenti i rettangoli di ciascuna di esse e della relativa parte esterna.
Teorema della tangente
Se da un punto esterno si conducono una tangente ed una secante ad un cerchio, la tangente è media proporzionale fra l'intera secante e la sua parte esterna.
Siano PT la tangente, PB e PA l'intera secante e la sua parte esterna. Si deve dimostrare che:

Infatti, i due triangoli PTA, PBT sono simili in quanto hanno l'angolo in P in comune, l'angolo in T e lati TP, TB uguale all'angolo in A e lati AP, AT come angoli alla circonferenza che insistono sullo stesso arco
PA : PT = PT : PB,
come volevasi dimostrare.
Corollario - Se da un punto esterno si conducono una tangente ed una secante ad un cerchio, il quadrato costruito sulla tangente è equivalente al rettangolo dell'intera secante e della parte esterna.
Costruzione del medio proporzionale
Costruire il segmento medio proporzionale fra due segmenti dati.
1° Modo: siano a e b due segmenti su una retta OA, da bande opposte rispetto ad un punto O, si costruiscono i segmenti OA = a, OB = b. Si descrive una semicirconferenza avente per diametro AB e sia C il punto in cui la perpendicolare da O ad OB incontra tale semicirconferenza.
Si deve dimostrare che OC è il segmento medio proporzionale fra OA e OB, ossia fra a e b.

Infatti, si congiunge C con A e con B, essendo il rettangolo ABC rettangolo in C, per il secondo teorema di Euclide, si ha:
2° Modo: siano a e b due segmenti su una retta OA, da una stessa banda rispetto ad un punto O, si costruiscono i segmenti OA = a, OB = b. Se OA> OB, si descrive una semicirconferenza avente per diametro OA. Sia C il punto in cui la perpendicolare da B ad OB incontra tale semicirconferenza.
Si deve dimostrare che OC è il segmento medio proporzionale fra OA e OB, ossia fra a e b.
Infatti, si congiunge C con O e con A, essendo il rettangolo OCA rettangolo in C, perchè inscritto nella semicirconferenza, per il primo teorema di Euclide, si ha:
Parte aurea di un segmento
Definizione - Si chiama parte aurea di un segmento quella parte che è media proporzionale fra l'intero segmento e la parte rimanente,
Costruzione della parte aurea di un segmento
Sia assegnato un segmento AB; dall'estremo B si conduce la perpendicolare ad AB e su di essa si considera un segmento BO uguale alla metà di AB. Puntando nel centro O e con raggio uguale ad OB, si descrive una circonferenza; essa risulta tangente ad AB in B. Si congiunge A con O e sia C il punto in cui il segmento OA incontra la circonferenza. Costruito AD = AC, si deve dimostrare che: AD è la parte aurea del segmento AB.

Infatti, prolungando AO fino ad incontrare in E la circonferenza, per il teorema della tangente si ha:
e dividendo
(AE - AB) : AB = (AB - AC) : AC.
Essendo
AB = CE e AC = AD,
si ha:
AE - AB = AE - CE = AC = AD
e
AB - AC = AB - AD = DB.
Dunque la proporzione precedente si può scrivere:
AD : AB = DB : AD
e invertendo, si ha
AB : AD = AD : DB.
Quindi AD è la parte aurea di AB.
Nota bene
Un segmento che è diviso in due parti di cui una sia la parte aurea, si dice che è diviso in media ed estrema ragione.
Costruzione del decagono regolare
Teorema - Il lato del decagono regolare inscritto in un cerchio è uguale alla parte aurea del raggio del cerchio stesso.
Siano OA, OB i raggi di un cerchio di centro O ed AB il lato del decagono regolare in esso inscritto.
Si deve dimostrare che AB è la parte aurea di OA.

Nel triangolo isoscele AOB l'angolo in O, essendo la decima parte dell'angolo giro, è 1/5 di un angolo piatto e allora ciascuno degli angoli uguali di vertice A e lati AO, AB e di vertice B e lati BO, BA è 2/5 di un angolo piatto. Perciò, se si traccia la bisettrice BC, gli angoli di vertice B e lati BO, BC e di vertice B e lati BC, BA sono ciascuno 1/5 di un angolo piatto, cioè uguali all'angolo in O. Si deduce che il triangolo OBC risulta isoscele sulla base OB. Inoltre, essendo l'angolo in C e lati CB, CA uguale a 2/5 di un angolo piatto, esso risulta uguale all'angolo di vertice A e lati AB, AC e allora il triangolo ABC risulta isoscele sulla base AC. Segue quindi che OC = BC, come lati del triangolo isoscele OCB e BC = AB, come lati del triangolo isoscele ABC. Da queste due uguaglianze, si ricava OC = AB. D'altra parte, dai triangoli simili OAB e BAC, si ha:
OA : AB = AB : CA
e ponendo, per l'uguaglianza precedente, OC al posto di AB, si ottiene:
OA : OC = OC : CA.
Da questa importante proporzione risulta che OC è uguale alla parte aurea del raggio; quindi anche AB, uguale al lato del decagono regolare, è uguale alla parte aurea del raggio.
La costruzione del decagono regolare inscritto in un cerchio risulta senz'altro da questo teorema.

Si conduce per O il raggio OB perpendicolare al raggio OA del cerchio dato e, diviso OB in due parti uguali mediante il punto C, si congiunge A con C. Puntando in C, e raggio CO, si descrive un arco di cerchio in modo che tagli AC in D. AD è uguale alla sezione aurea del raggio e quindi al lato del decagono regolare.
Costruzione del pentagono regolare
Si
divide la circonferenza in 10 parti uguali mediante la costruzione
precedente e si congiungono i punti di divisione a due a due
alternativamente, si ottiene il pentagono regolare.

Poligoni simili
Definizione - Due poligoni si dicono simili se hanno gli angoli ordinatamente uguali e i lati omologhi proporzionali.
Si chiamano omologhi i lati di due poligoni simili che hanno come estremi i vertici di angoli uguali.
Si dice rapporto di similitudine il rapporto fra due lati omologhi qualsiasi.
Dalla definizione si ricava:
1)-la similitudine fra due poligoni gode della proprietà riflessiva, simmetrica e transitiva.
2)-i poligoni regolari dello stesso numero di lati sono simili.

Teorema - Se in due poligoni simili da due vertici corrispondenti si conducono tutte le possibili diagonali, i poligoni restano divisi nello stesso numero di triangoli ordinatamente simili.
Siano ABCDE, A'B'C'D'E' i poligoni simili e si abbia:
ed inoltre
AB : A'B' = BC : B'C' = ....
Dopo aver tracciato le diagonali AC, AD e le corrispondenti A'C', AC'D', si deve dimostrare che i triangoli ABC, ACD, ADE sono ordinatamente simili ai triangoli A'B'C', A'C'D', A'D'E'.
Dopo aver tracciato le diagonali AC, AD e le corrispondenti A'C', AC'D', si deve dimostrare che i triangoli ABC, ACD, ADE sono ordinatamente simili ai triangoli A'B'C', A'C'D', A'D'E'.

Infatti, i triangoli ABC, A'B'C' sono simili, perchè hanno gli angoli in B e in B' uguali e i lati AB, BC e A'B' B'C', che li comprendono, proporzionali. Segue quindi:
(1) BC : B'C' = AC : A'C'
e che
Si tiene conto ora che, per ipotesi risulta:
QuindI, sottraendo membro a membro questa uguaglianza dalla precedente, si ha:
ossia
Inoltre, poichè per ipotesi risuta ancora:
BC : B'C' = CD : C'D',
confrontando questa proporzione con la (1), si vede che le due proporzioni hanno i primi due rapporti uguali; quindi gli altri due rapporti formano la proporzione
AC = A'C' = CD : C'D'.
I due triangoli ACD, A'C'D' sono quindi simili, perchè hanno un angolo uguale
e i lati che lo comprendono in proporzione.
Analogamente si dimostra che sono simili gli altri triangoli.
Teorema - I perimetri di due poligoni simili stanno fra loro come due lati corrispondenti qualsiasi.
Siano ABCDE, A'B'C'D'E' due poligoni simili di perimetri P e P'. Si deve dimostrare che:
Infatti, nella figura precedente, per la similitudine dei poligoni, si ha:
e da questa catena di rapporti si ricava
ossia
come volevasi dimostrare.
Teorema - Due poligoni simili stanno fra loro come i quadrati di due lati corrispondenti.
1)-Si dimostra il teorema nel caso dei triangoli.
Siano ABC, A'B'C' due triangoli simili, si deve dimostrare che:
Infatti, indicando con a e a' le misure dei due lati corrispondenti AB, A'B', con h e h' le misure delle relative altezze e con S, S' le misure dei triangoli, cioè le loro aree, si ha:
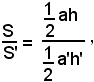
ossia (1)
Inoltre, per il teorema dimostrato in precedenza "in due triangoli simili le altezze condotte da due vertici omologhi sono proporzionali a due lati omologhi qualsiasi", si ha:
e, sostituendo in (1) al rapporto
il valore precedente, si ha:
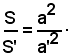
E' così dimostrato che le aree dei triangoli, e quindi i triangoli stessi, stanno come i quadrati dei loro due lati corrispondenti.
2)-Si dimostra il teorema nel caso generale di due poligoni.
Siano dati i due poligoni ABCDE, A'B'C'D'E'
Si deve dimostrare che:
ABCDE : A'B'C'D'E = q(AB) : q(A'B').

Infatti, se da due vertici corrispondenti, A, A' si tracciano tutte le possibili diagonali, i due poligoni vengono scomposti nello stesso numero di triangoli ordinatamente simili. Si indicano con R, S, T, i triangoli nei quali viene scomposto il primo poligono e con R', S', T' quelli in cui viene scomposto il secondo. Per la prima parte di questo teorema, si ha:
R : R' = q(AC) : q(A'C')
e
S : S' = q(AC) : q(A'C').
Per il teorema dimostrato in precedenza "due coppie di grandezze proporzionali ad una terza sono proporzionali fra loro", si ha:
Analogamente si dimostra che
Tenendo conto delle due proporzioni precedenti:
R : R' = S : S' = T : T'
ed ancora si ha:
(R + S + T) : (R' + S' + T') = R : R',
ossia
ABCDE : A'B'C'D'E' = R : R'
ma essendo:
R : R' = q(AB) : q(A'B'),
si conclude perciò che:
Teorema - I perimetri di due poligoni regolari dello stesso numero di lati stanno fra loro come i lati, come i raggi, come gli apotemi.
Siano ABCDE, A'B'C'D'E' due poligoni regolari dello stesso numero di lati, ad esempio 5, OH e O'H' gli apotemi, OA e O'A' i raggi, P, P' i perimetri.
Si deve dimostrare che:
P : P' = AB : A'B' = OA : O'A' = OH: O'H'.

Infatti, due poligoni regolari, aventi lo stesso numero di lati, essendo simili, si ha:
P : P' = AB : A'B'.
Inoltre i due triangoli OAH, O'A'H' sono simili perchè sono rettangoli ed hanno gli angoli acuti in O, O' uguali in quanto metà di angoli uguali; perciò si ha:
AH : A'H' = OA : O'A' = OH : O'H'
e raddoppiando i termini del primo rapporto:
AB : A'B' = OA : O'A' = OH: O'H',
cioè i lati stanno fra loro come i raggi e come gli apotemi e, siccome i perimetri stanno fra loro come i lati, il teorema è dimostrato.
Teorema - Due poligoni regolari dello stesso numero di lati stanno fra loro come i quadrati dei lati omologhi, dei raggi, degli apotemi.
Siano S ed S' due poligoni regolari, di cui AB, A'B' siano due lati, OA e O'A' due raggi ed OH, O'H' i due apotemi, fra loro corrispondenti. Per il teorema "due poligoni simili stanno fra loro come i quadrati dei lati corrispondenti", si ha.
S : S' = q(AB) : q(A'B').
Siccome per il teorema precedente:
anche i quadrati di questi segmenti sono in proporzione, cioè:
Tenendo conto della proporzione (1), si può concludere che:
come volevasi dimostrare.