MIKY & GENNY
TEOREMI DI EUCLIDE E DI PITAGORA ---> INDICE
PRIMO TEOREMA DI EUCLIDE
Il
quadrato costruito su un cateto di un triangolo rettangolo è
equivalente al rettangolo che ha per lati l'ipotenusa e la proiezione
del cateto sull'ipotenusa.
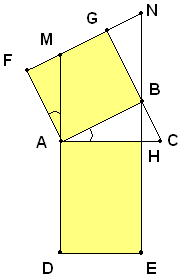
Ipotesi: dato un triangolo ABC, rettangolo in B, si costruisce il quadrato ABGF sul cateto AB, dalla parte opposta del triangolo dato ed il rettangolo AHED in cui un lato AH è la proiezione di AB sull'ipotenusa, mentre il lato consecutivo AD è uguale all'ipotenusa AC del triangolo dato.
Tesi: si vuole dimostrare che il quadrato ABGF è equivalente al rettangolo AHED, cioè, se si indica con q(AB) il quadrato costruito su AB e con r(AH, AD) il rettangolo che ha per lati consecutivi AH e AD, che: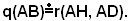
Dimostrazione
Ipotesi: dato un triangolo ABC, rettangolo in B, si costruisce il quadrato ABGF sul cateto AB, dalla parte opposta del triangolo dato ed il rettangolo AHED in cui un lato AH è la proiezione di AB sull'ipotenusa, mentre il lato consecutivo AD è uguale all'ipotenusa AC del triangolo dato.
Tesi: si vuole dimostrare che il quadrato ABGF è equivalente al rettangolo AHED, cioè, se si indica con q(AB) il quadrato costruito su AB e con r(AH, AD) il rettangolo che ha per lati consecutivi AH e AD, che:
Dimostrazione
Si
prolungano DA e EH fino ad incontrare nei punti M e N la retta del lato
FG e si forma il parallelogrammo ABNM. Si comincia col dimostrare che
AM=AD. Pertanto, si considerano i triangoli AFM e ABC, rettangoli in F
e B rispettivamente; essi hanno uguali, per costruzione, i cateti AF e
AB e uguali gli angoli acuti FAM e BAC, perchè complementari
dello stesso angolo MAB; sono quindi uguali ed hanno perciò
uguali ipotenuse AM e AC. Siccome AC è uguale a AD per
costruzione, dunque anche AM=AD. Premesso ciò, si confronta il
quadrato ABGF col parallelogrammo ABNM e poi quest'ultimo col rettangolo ADEH. Il quadrato e il parallelogrammo sono equivalenti, perchè hanno la base AB in comune e la stessa altezza BG; il
parallelogrammo e il rettangolo sono anche equivalenti perchè
hanno le basi AD e AM uguali, come è noto, e
la stessa altezza AH, la quale è la distanza fra le parallele DM
e EN. Dunque sussistono le relazioni seguenti:
1)-il quadrato ABGF è equivalente al parallelogrammo ABNM,
2)-il parallelogrammo ABNM è equivalente al rettangolo ADEH.
Segue, per la proprietà transitiva, che il quadrato ABGF è equivalente al rettangolo ADEH, come volevasi dimostrare.
Il quadrato costruito sull'ipotenusa di un triangolo rettangolo è equivalente alla somma dei quadrati costruiti sui cateti.
Ipotesi: dato un triangolo ABC, rettangolo in B.
Tesi: si vuole dimostrare che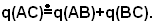
Dimostrazione
1)-il quadrato ABGF è equivalente al parallelogrammo ABNM,
2)-il parallelogrammo ABNM è equivalente al rettangolo ADEH.
Segue, per la proprietà transitiva, che il quadrato ABGF è equivalente al rettangolo ADEH, come volevasi dimostrare.
TEOREMA DI PITAGORA
Il quadrato costruito sull'ipotenusa di un triangolo rettangolo è equivalente alla somma dei quadrati costruiti sui cateti.
Ipotesi: dato un triangolo ABC, rettangolo in B.
Tesi: si vuole dimostrare che
Dimostrazione
Infatti,
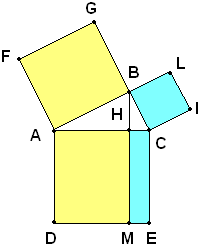
si abbassa da B la perpendicolare BH all'ipotenusa e si prolunga fino
ad incontrare il lato DE nel quadrato costruito su AC nel punto M. Il
quadrato sull'ipotenusa viene così diviso in nei rettangoli ADMH
e HMEC. Per il teorema di Euclide, il rettangolo ADMH è equivalente al quadrato costruito su AB e il rettangolo HMEC è equivalente al quadrato costruito su BC, cioè:
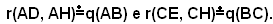
Segue
che la somma dei rettangoli suddetti, cioè il quadrato
costruito su AC è equivalente alla somma dei quadrati costruiti
su AB e BC:
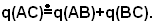
Il teorema è così dimostrato.
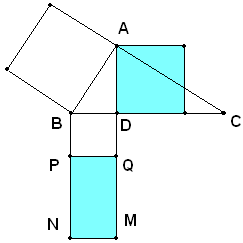
Il quadrato costruito sull'altezza relativa all'ipotenusa di un triangolo rettangolo è equivalente al rettangolo delle due parti in cui divide l'ipotenusa.
Ipotesi: dato un triangolo ABC, rettangolo in A, sia BC l'altezza relativa all'ipotenusa BC.
Tesi: si vuole dimostrare che il quadrato AD è equivalente al rettangolo che ha per lati BD e DC, cioè: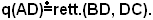
Dimostrazione
Si costruisce il quadrato dell'altezza AD, il lato BN è uguale all'ipotenusa BC. Sul lato BN si prende il segmento BP uguale a AD e si traccia la parallela PQ a BC; si formano così il quadrato BPDQ e il rettangolo PQMN e risulta: PN=BN-BP=BC-BD=DC. Allora, il triangolo PQMN ha i due lati PQ e PN rispettivamente uguali alle proiezioni BD e DC dei due cateti sull'ipotenusa. Si tratta di dimostrare che il quadrato di AD è equivalente al rettangolo PQMN. Ora, per il primo teorema di Euclide, applicato al triangolo rettangolo ABC, si ha: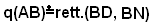
, ossia:
.
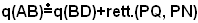Per il teorema di Pitagora, applicato al triangolo ABD, si ha:
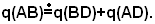
SECONDO TEOREMA DI EUCLIDE
Il quadrato costruito sull'altezza relativa all'ipotenusa di un triangolo rettangolo è equivalente al rettangolo delle due parti in cui divide l'ipotenusa.
Ipotesi: dato un triangolo ABC, rettangolo in A, sia BC l'altezza relativa all'ipotenusa BC.
Tesi: si vuole dimostrare che il quadrato AD è equivalente al rettangolo che ha per lati BD e DC, cioè:
Dimostrazione
Si costruisce il quadrato dell'altezza AD, il lato BN è uguale all'ipotenusa BC. Sul lato BN si prende il segmento BP uguale a AD e si traccia la parallela PQ a BC; si formano così il quadrato BPDQ e il rettangolo PQMN e risulta: PN=BN-BP=BC-BD=DC. Allora, il triangolo PQMN ha i due lati PQ e PN rispettivamente uguali alle proiezioni BD e DC dei due cateti sull'ipotenusa. Si tratta di dimostrare che il quadrato di AD è equivalente al rettangolo PQMN. Ora, per il primo teorema di Euclide, applicato al triangolo rettangolo ABC, si ha:
, ossia:.Per il teorema di Pitagora, applicato al triangolo ABD, si ha:
Allora le due somme, essendo entrambe equivalenti a q(AB), sono equivalenti fra loro:
Togliendo da queste due somme la parte comune q(BD), risulta: 
, come volevasi dimostrare.
, come volevasi dimostrare.