MIKY & GENNY
FORMULE DI PROSTAFERESI ---> INDICE
Nelle
applicazioni pratiche è preferibile avere espressioni contenenti
il prodotto o il quoziente di funzioni goniometriche, anzichè la
loro somma.
La trasformazione di espressioni in cui figurano somme o differenze, in altre contenenti prodotti o quozienti, si ottiene mediante le formule di prostaferesi.
Per ricavarle, si considerano le formule di addizione e sottrazione degli angoli, di seguito riportate:
sen(α + β) = senαcosβ + cosαsenβ,
sen(α - β) = senαcosβ - cosαsenβ,
cos(α + β) = cosαcosβ - senαsenβ,
cos(α - β) = cosαcosβ + senαsenβ,
sommando membro a membro le prime due e le ultime due, si ottengono le formule (1):
sen(α + β) + sen(α - β) = 2senαcosβ,
sen(α + β) - sen(α - β) = 2 cosαsenβ,
cos(α + β) + cos(α - β) = 2cosαcosβ
cos(α + β) - cos(α - β) = -2senαsenβ.
Posto α + β = p e α - β = q, risolvendo rispetto ad α e β, si ricava:
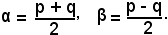
Sostituendo i valori di p e q nelle formule (1), si hanno le formule (2):
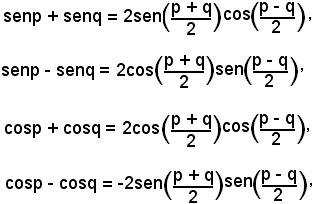
chiamate formule di prostaferesi. Esse trasformano la somma o la differenza dei seni e dei coseni in prodotti.
Nota bene
La parola prostaferesi è composta da due parole greche: aggiunta e diminuzione e significa appunto "somma e sottrazione".
Le (2) si possono estendere in generale ad altre espressioni.
Infatti, considerate le espressioni del tipo
senp ± cosq,
evidentemente si può scrivere
senp ± cosq = senp ± sen(90° - q),
oppure
senp ± cosq = cos(90° - p) ± cosq.
Applicando le (2), si ha:
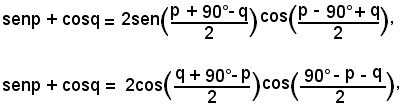
ed analogamente per gli altri casi. Inoltre,
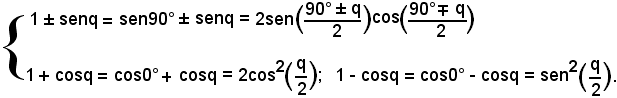
Più in generale, si possono trasformare in prodotti i binomi della forma
a ± senq, a ± cosq,
tutte le volte che |a| < 1.
Infatti, se |a| ≤ 1, esiste sempre almeno un angolo p, compreso fra 0° e 360°, tale che tisulti
a = senp, oppure a = cosp,
e, di conseguenza, le espressioni precedenti si trasformano in
a ± senq = senp ± senq, a ± cosq = cosp ± cosq,
che rientrano nella formula (2).
Si stabiliscono ora le formule di prostasferesi relative alla tangente e alla cotangente, cioè (3):

Anche queste formule, come le precedenti, si possono generalizzare, osservando che
tgp ± ctgq = tgp ± tg(90° - q),
tgp ± ctgq = ctg(90° - p) ± ctgq.
Più in generale, possono rientrare nelle (3) le espressioni
a ± tgq, a ± ctgq,
con a numero reale qualsiasi.
Infatti, considerato a numero reale qualsiasi, esiste sempre almeno un angolo p, compreso fra 0° e 180°, tale che risulti
a = tgp, oppure a = ctgp,
allora si ha:
a ± tgq = tgp ± tgq, a ± ctgq = ctgp ± ctgq.
In particolare:
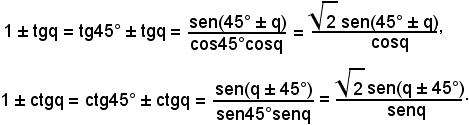
Nelle applicazioni pratiche risultano molto utili le formule di Nepero, che si ottengono come segue:
si considera l'espressione
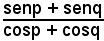
e si applicano le formule di prostaferesi al numeratore e al denominatore, si ha:
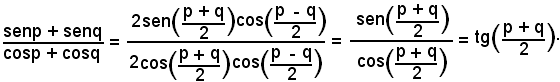
Analogamente:
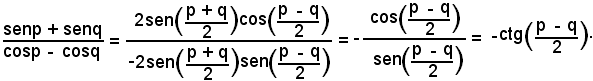
Si procede allo stesso modo per le seguenti espressioni, delle quali non si riportano i calcoli:
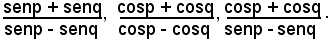
Nota storica
John Nepero o Napier, nacque ad Edimburgo nel 1550 e morì nel 1617. Egli scoprì i logaritmi e pubblicò per primo una loro tavola, prendendo per base un numero molto prossimo al numero e (di Eulero) intitolata "Mirifici logarithmorum canonis descriptio, eiusque usus in utraque trigonometria" (Edimburgo 1614).
Le formule riportate nel testo sono dette impropriamente formule di Nepero, perchè analoghe a quelle che egli pubblicò per primo, relativamente agli elementi di un triangolo sferico.
Quelle del testo sono dovute a Bartolomeo Pitisco, nato a Grunberg nel 1561 e morto ad Heidelberg nel 1613, la cui fama è dovuta per aver pubblicato, ampliandole, le tavole dei valori naturali dei seni e delle tangenti di 10 secondi in 10 secondi, con 10 cifre decimali, dovute a Giorgio Joaquim, nato nel 1514 a Feldkirch nel Voralberg, detto il Retico dal nome latino della regione, e morto a Cassovia nel 1576.
La fama del Retico consiste, oltre che nell'aver curato la pubblicazione delle opere di Copernico, nell'aver stabilito le espressioni di sen(2α) e sen(3α) e definito le funzioni trigonometriche senza ricorrere al cerchio, mediante i rapporti tra i lati di un triangolo rettangolo. Egli pubblicò tali risultati nel 1551 nel suo trattato "Canon doctrinae triangulorum".
La trasformazione di espressioni in cui figurano somme o differenze, in altre contenenti prodotti o quozienti, si ottiene mediante le formule di prostaferesi.
Per ricavarle, si considerano le formule di addizione e sottrazione degli angoli, di seguito riportate:
sen(α + β) = senαcosβ + cosαsenβ,
sen(α - β) = senαcosβ - cosαsenβ,
cos(α + β) = cosαcosβ - senαsenβ,
cos(α - β) = cosαcosβ + senαsenβ,
sommando membro a membro le prime due e le ultime due, si ottengono le formule (1):
sen(α + β) + sen(α - β) = 2senαcosβ,
sen(α + β) - sen(α - β) = 2 cosαsenβ,
cos(α + β) + cos(α - β) = 2cosαcosβ
cos(α + β) - cos(α - β) = -2senαsenβ.
Posto α + β = p e α - β = q, risolvendo rispetto ad α e β, si ricava:
Sostituendo i valori di p e q nelle formule (1), si hanno le formule (2):
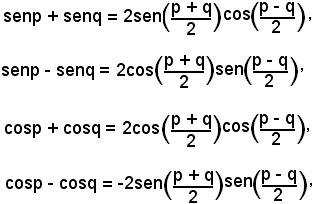
chiamate formule di prostaferesi. Esse trasformano la somma o la differenza dei seni e dei coseni in prodotti.
Nota bene
La parola prostaferesi è composta da due parole greche: aggiunta e diminuzione e significa appunto "somma e sottrazione".
Le (2) si possono estendere in generale ad altre espressioni.
Infatti, considerate le espressioni del tipo
senp ± cosq,
evidentemente si può scrivere
senp ± cosq = senp ± sen(90° - q),
oppure
senp ± cosq = cos(90° - p) ± cosq.
Applicando le (2), si ha:
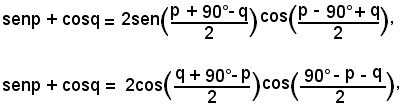
ed analogamente per gli altri casi. Inoltre,
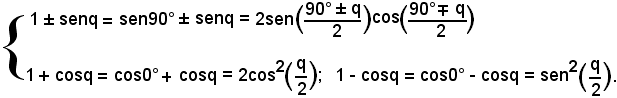
Più in generale, si possono trasformare in prodotti i binomi della forma
tutte le volte che |a| < 1.
Infatti, se |a| ≤ 1, esiste sempre almeno un angolo p, compreso fra 0° e 360°, tale che tisulti
e, di conseguenza, le espressioni precedenti si trasformano in
a ± senq = senp ± senq, a ± cosq = cosp ± cosq,
che rientrano nella formula (2).
Si stabiliscono ora le formule di prostasferesi relative alla tangente e alla cotangente, cioè (3):

Anche queste formule, come le precedenti, si possono generalizzare, osservando che
tgp ± ctgq = tgp ± tg(90° - q),
tgp ± ctgq = ctg(90° - p) ± ctgq.
Più in generale, possono rientrare nelle (3) le espressioni
a ± tgq, a ± ctgq,
con a numero reale qualsiasi.
Infatti, considerato a numero reale qualsiasi, esiste sempre almeno un angolo p, compreso fra 0° e 180°, tale che risulti
a = tgp, oppure a = ctgp,
allora si ha:
a ± tgq = tgp ± tgq, a ± ctgq = ctgp ± ctgq.
In particolare:
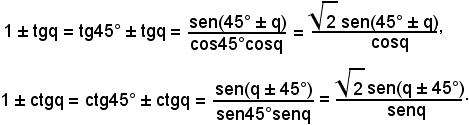
si considera l'espressione
e si applicano le formule di prostaferesi al numeratore e al denominatore, si ha:
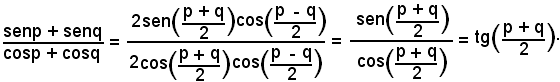
Analogamente:
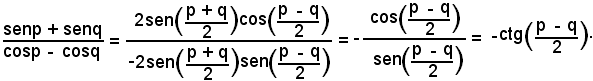
Si procede allo stesso modo per le seguenti espressioni, delle quali non si riportano i calcoli:
Nota storica
John Nepero o Napier, nacque ad Edimburgo nel 1550 e morì nel 1617. Egli scoprì i logaritmi e pubblicò per primo una loro tavola, prendendo per base un numero molto prossimo al numero e (di Eulero) intitolata "Mirifici logarithmorum canonis descriptio, eiusque usus in utraque trigonometria" (Edimburgo 1614).
Le formule riportate nel testo sono dette impropriamente formule di Nepero, perchè analoghe a quelle che egli pubblicò per primo, relativamente agli elementi di un triangolo sferico.
Quelle del testo sono dovute a Bartolomeo Pitisco, nato a Grunberg nel 1561 e morto ad Heidelberg nel 1613, la cui fama è dovuta per aver pubblicato, ampliandole, le tavole dei valori naturali dei seni e delle tangenti di 10 secondi in 10 secondi, con 10 cifre decimali, dovute a Giorgio Joaquim, nato nel 1514 a Feldkirch nel Voralberg, detto il Retico dal nome latino della regione, e morto a Cassovia nel 1576.
La fama del Retico consiste, oltre che nell'aver curato la pubblicazione delle opere di Copernico, nell'aver stabilito le espressioni di sen(2α) e sen(3α) e definito le funzioni trigonometriche senza ricorrere al cerchio, mediante i rapporti tra i lati di un triangolo rettangolo. Egli pubblicò tali risultati nel 1551 nel suo trattato "Canon doctrinae triangulorum".