MIKY & GENNY
GRAFICI DELLE FUNZIONI GONIOMETRICHE ---> INDICE
1)-Curva del seno o sinusoide
Si indichi con y il valore che assume la funzione senx per un assegnato valore x dell'angolo, cioè si pone:
(1) y = senx,
ove l'angolo x deve intendersi misurato in radianti.Se
si considerano x ed y come le coordinate cartesiane di un punto
del piano, come visto in precedenza, la (1) ha un grafico che si chiama
curva del seno o sinusoide.
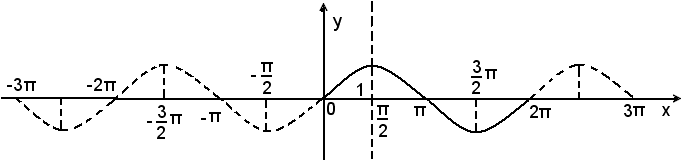
Per avere un'idea di tale curva, si osserva innanzitutto che basta conoscere la forma per tutti i valori della variabile, compresi tra 0 e 2π, per ottenere tutto l'andamento.
Infatti, ricordando la periodicità della funzione seno espressa dalla relazione:
sen(x + 2kπ) = senx,
una volta tracciata la sinusoide per i valori compresi tra 0 e 2π, basta imprimere a tale grafico, lungo l'asse x, da una parte e dall'altra, una successione di traslazioni di ampiezza 2π, per ottenere l'intera curva. Successivamente, se si tiene presente dell'altra relazione:
sen(x + π) = -senx,
è chiaro che, tracciato il grafico per i valori di x tali che 0 ≤ x ≤ π, si ottiene anche quello relativo ai valori di x compresi tra π e 2π, traslando il grafico ottenuto, sempre lungo l'asse x, di un tratto π, e ribaltandolo intorno allo stesso asse.
Si osserva infine che, essendo i due angoli
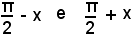
fra loro supplementari, vale la relazione
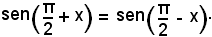
E' evidente che, tracciato il grafico per valori della x compresi tra 0 e π/2, basta ribaltarlo intorno alla parallela all'asse delle y, passante per il punto di ascissa π/2 dell'asse delle x, per ottenere il grafico relativo ai valori della x compresi tra 0 e π. Quindi, per quanto detto, l'intera sinusoide appare nella figura suddetta.
Costruzione approssimata della sinusoide per punti
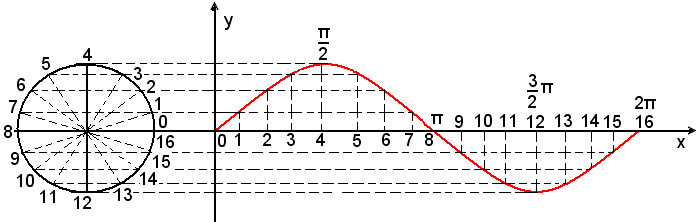
A partire dall'origine, tracciato sull'asse delle x un segmento lungo 2π, rispetto al raggio del cerchio trigonometrico scelto come unità di misura, si possono ottenere i punti desiderati della sinusoide, mediante una semplicissima costruzione.
Allo scopo, si divide la circonferenza, ad esempio, in 16 = 24 parti uguali, usando riga e compasso, mediante punti indicati 0, 1, 2, 3, ..., 14, 15, 16; e corrispondentemente si divide un segmento dell'asse delle x, lungo 2π, in altrettante parti uguali, mediante punti indicati anche con 0, 1, 2, 3, ..., 14, 15, 16.
Le rette congiungenti le coppie di punti 1 e 7; 2 e 6; 3 e 5; 9 e 15; 10 e 14; 11 e 13 della circonferenza sono parallele all'asse delle x; a tale asse si conduce anche la parallela dai punti 4 e 12 della circonferenza. Dai punti 1, 2, ..., 15, 16 dell'asse delle x si tracciano le parallele all'asse delle y fino ad incontrare le parallele precedenti, corrispondenti agli stessi numeri d'ordine.
I punti d'intersezione così ottenuti appartengono alla sinusoide.
2)-Curva del coseno o cosinusoide
Per ottenere il grafico della funzione
(2) y = cosx,
detto curva del coseno o cosinusoide, si osserva che, essendo gli angoli x + π/2 e -x complementari, vale la relazione
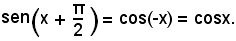
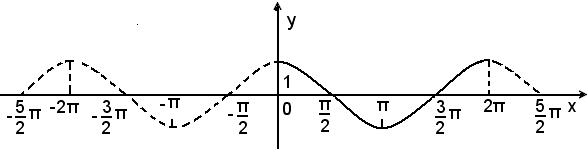
Il grafico si ottiene quindi dalla sinusoide mediante una traslazione di ampiezza -π/2 lungo l'asse delle x; la cosinusoide è rappresentata nella figura seguente:
3)-Curva della tangente o tangentoide
Per ottenere il grafico della funzione
(3) y = tgx,
detto curva della tangente o tangentoide, si deve tenere presente la periodicità della funzione tangente, espressa dalla relazione
tg(x + kπ) = tgx.
Ripetendo un ragionamento analogo a quello della sinusoide, basta tracciare il grafico solo per i valori della variabile x compresi tra 0 e π.
Inoltre, tenendo presente che
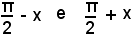
sono supplementari, in virtù dell'ulteriore relazione
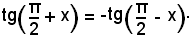
si può dire che, tracciato il tratto di tangentoide relativo ai valori di x compresi fra 0 e π/2, basta traslarlo lungo l'asse delle x di un tratto di ampiezza π/2 e ribaltarlo intorno all'asse delle x, per ottenere tutta la tangentoide, rappresentata nella seguente figura:
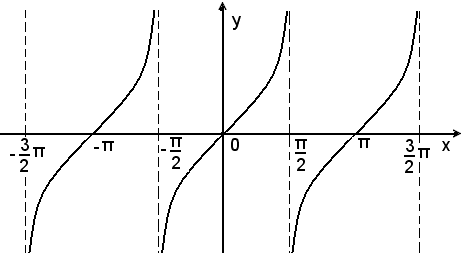
Costruzione approssimata della tangentoide per punti
Anche per la tangentoide si può seguire un procedimento semplicissimo per ottenere i suoi punti nel numero desiderato.
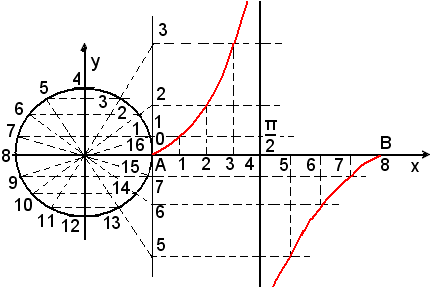
Ad esempio, si divide la circonferenza in 16 = 24 parti uguali, usando riga e compasso, si stacca poi sul prolungamento del raggio OA, a partire da A, un segmento AB lungo π, e da A si conduce la tangente al cerchio trigonometrico.
Si divide il segmento AB dell'asse delle x in 8 parti uguali, indicando i punti di divisione con i numeri 0, 1, 2, ..., 7, 8.
Successivamente si prolungano i raggi della circonferenza che vanno ai suoi punti di divisione fino ad incontrare la tangente in A, indicando su questa i punti d'intersezione con i numeri 0, 1, 2, ..., 7, 8.
Infine, da questi punti si conducono le parallele all'asse delle x intersecandole con le perpendicolari allo stesso asse, uscenti dai punti indicati con gli stessi numeri. I punti d'intersezione così ottenuti appartengono alla tangentoide.
4)-Curva della cotangente o cotangentoide
Per ottenere il grafico della funzione
(4) y = ctgx,
detto curva della cotangente o cotangentoide, si osserva che, dalla relazione
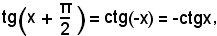
risulta evidente che questa si può ottenere dalla tangentoide mediante una traslazione lungo l'asse delle x.
Si indichi con y il valore che assume la funzione senx per un assegnato valore x dell'angolo, cioè si pone:
(1) y = senx,
ove l'angolo x deve intendersi misurato in radianti.
Per avere un'idea di tale curva, si osserva innanzitutto che basta conoscere la forma per tutti i valori della variabile, compresi tra 0 e 2π, per ottenere tutto l'andamento.
Infatti, ricordando la periodicità della funzione seno espressa dalla relazione:
sen(x + 2kπ) = senx,
una volta tracciata la sinusoide per i valori compresi tra 0 e 2π, basta imprimere a tale grafico, lungo l'asse x, da una parte e dall'altra, una successione di traslazioni di ampiezza 2π, per ottenere l'intera curva. Successivamente, se si tiene presente dell'altra relazione:
sen(x + π) = -senx,
è chiaro che, tracciato il grafico per i valori di x tali che 0 ≤ x ≤ π, si ottiene anche quello relativo ai valori di x compresi tra π e 2π, traslando il grafico ottenuto, sempre lungo l'asse x, di un tratto π, e ribaltandolo intorno allo stesso asse.

Si osserva infine che, essendo i due angoli
fra loro supplementari, vale la relazione
E' evidente che, tracciato il grafico per valori della x compresi tra 0 e π/2, basta ribaltarlo intorno alla parallela all'asse delle y, passante per il punto di ascissa π/2 dell'asse delle x, per ottenere il grafico relativo ai valori della x compresi tra 0 e π. Quindi, per quanto detto, l'intera sinusoide appare nella figura suddetta.
Costruzione approssimata della sinusoide per punti
A partire dall'origine, tracciato sull'asse delle x un segmento lungo 2π, rispetto al raggio del cerchio trigonometrico scelto come unità di misura, si possono ottenere i punti desiderati della sinusoide, mediante una semplicissima costruzione.
Allo scopo, si divide la circonferenza, ad esempio, in 16 = 24 parti uguali, usando riga e compasso, mediante punti indicati 0, 1, 2, 3, ..., 14, 15, 16; e corrispondentemente si divide un segmento dell'asse delle x, lungo 2π, in altrettante parti uguali, mediante punti indicati anche con 0, 1, 2, 3, ..., 14, 15, 16.
Le rette congiungenti le coppie di punti 1 e 7; 2 e 6; 3 e 5; 9 e 15; 10 e 14; 11 e 13 della circonferenza sono parallele all'asse delle x; a tale asse si conduce anche la parallela dai punti 4 e 12 della circonferenza. Dai punti 1, 2, ..., 15, 16 dell'asse delle x si tracciano le parallele all'asse delle y fino ad incontrare le parallele precedenti, corrispondenti agli stessi numeri d'ordine.
I punti d'intersezione così ottenuti appartengono alla sinusoide.

2)-Curva del coseno o cosinusoide
Per ottenere il grafico della funzione
detto curva del coseno o cosinusoide, si osserva che, essendo gli angoli x + π/2 e -x complementari, vale la relazione
Il grafico si ottiene quindi dalla sinusoide mediante una traslazione di ampiezza -π/2 lungo l'asse delle x; la cosinusoide è rappresentata nella figura seguente:

3)-Curva della tangente o tangentoide
Per ottenere il grafico della funzione
(3) y = tgx,
detto curva della tangente o tangentoide, si deve tenere presente la periodicità della funzione tangente, espressa dalla relazione
tg(x + kπ) = tgx.
Ripetendo un ragionamento analogo a quello della sinusoide, basta tracciare il grafico solo per i valori della variabile x compresi tra 0 e π.
Inoltre, tenendo presente che
sono supplementari, in virtù dell'ulteriore relazione
si può dire che, tracciato il tratto di tangentoide relativo ai valori di x compresi fra 0 e π/2, basta traslarlo lungo l'asse delle x di un tratto di ampiezza π/2 e ribaltarlo intorno all'asse delle x, per ottenere tutta la tangentoide, rappresentata nella seguente figura:

Costruzione approssimata della tangentoide per punti
Anche per la tangentoide si può seguire un procedimento semplicissimo per ottenere i suoi punti nel numero desiderato.

Ad esempio, si divide la circonferenza in 16 = 24 parti uguali, usando riga e compasso, si stacca poi sul prolungamento del raggio OA, a partire da A, un segmento AB lungo π, e da A si conduce la tangente al cerchio trigonometrico.
Si divide il segmento AB dell'asse delle x in 8 parti uguali, indicando i punti di divisione con i numeri 0, 1, 2, ..., 7, 8.
Successivamente si prolungano i raggi della circonferenza che vanno ai suoi punti di divisione fino ad incontrare la tangente in A, indicando su questa i punti d'intersezione con i numeri 0, 1, 2, ..., 7, 8.
Infine, da questi punti si conducono le parallele all'asse delle x intersecandole con le perpendicolari allo stesso asse, uscenti dai punti indicati con gli stessi numeri. I punti d'intersezione così ottenuti appartengono alla tangentoide.
4)-Curva della cotangente o cotangentoide
Per ottenere il grafico della funzione
(4) y = ctgx,
detto curva della cotangente o cotangentoide, si osserva che, dalla relazione
risulta evidente che questa si può ottenere dalla tangentoide mediante una traslazione lungo l'asse delle x.